サイトトップ
Director Flash 書籍 業務内容 プロフィール

HTML5テクニカルノート

EaselJSのGraphicsクラスで2次ベジエ曲線を描く

ID: FN1306002 Technique: HTML5 and JavaScript Library: EaselJS 0.6.1

Graphics.beginStroke()メソッド
文法 Graphicsオブジェクト.beginStroke(color)
概要 定められた色で線を描く。それまでのサブパスは閉じられる。
引数 color ー CSSにしたがった色指定の文字列。引数がないときは、線が描かれない。
戻り値 メソッドが呼出されたGraphicsオブジェクト。
Graphics.setStrokeStyle()メソッド
文法 Graphicsオブジェクト.setStrokeStyle(thickness, caps, joints, miterLimit, ignoreScale)
概要 現行のパスに描く線のスタイルを定める。
引数

thickness ー 線の太さ。

caps ー 線の端の形状を定める0から2までの整数または形状名の文字列。CanvasのlineCapプロパティに対応した次表001のかたちが選べる。

表001■整数値と線の端のかたち
整数値 形状名 端のかたち
0 butt 端の座標までの長さで切る(デフォルト)。
1 round 端の座標を中心とした直径が線の太さの半円で丸める。
2 square 端の座標から線の太さの半分だけ長さを延ばす。

joints ー 線が結ばれる角のかたちを0から2までの整数値または形状名の文字列で定める。 CanvasのlineJoinプロパティに対応した次表002のかたちが選べる。

表002■整数値と線の角のかたち
整数値 形状名 角のかたち
0 miter とがらせる(デフォルト)。
1 round 直径が線の太さの扇形をつけ加えて丸める。
2 bevel 平らに削る。

miterLimit ー 第3引数を0(miter)にした場合、結ぶ線のとがった角が伸びすぎないように、最大値を定める比率。比率は線の太さの半分を1とする。デフォルト値は10。最大値を超えた部分は削られる。CanvasのmiterLimitプロパティに対応する。

ignoreScale ー 変形が加わっても線の太さは保つかを定めるブール(論理)値。trueにすると、変形しても線の太さが変わらない。デフォルト値はfalse。
戻り値 メソッドが呼出されたGraphicsオブジェクト。
Graphics.moveTo()メソッド
文法 Graphicsオブジェクト.moveTo(x, y)
概要 描画し始める現行の座標を新たに定める。
引数

x − 描画を新たに始めるx座標値。

y − 描画を新たに始めるy座標値。
戻り値 メソッドが呼出されたGraphicsオブジェクト。
Graphics.quadraticCurveTo()メソッド
文法 Graphicsオブジェクト.quadraticCurveTo(cpx, cpy, x, y)
概要 現行の座標から第1および第2引数の座標(cpx, cpy)をコントロールポイントとして、第3および第4引数の座標(x, y)まで2次ベジエ曲線を描く。
引数

cpx − コントロールポイントのx座標値。

cpy − コントロールポイントのy座標値。

x − 曲線を結ぶx座標値。

y − 曲線を結ぶy座標値。
戻り値 メソッドが呼出されたGraphicsオブジェクト。
Graphics.curveTo()メソッド
文法 Graphicsオブジェクト.curveTo(cpx, cpy, x, y)
概要 現行の座標から第1および第2引数の座標(cpx, cpy)をコントロールポイントとして、第3および第4引数の座標(x, y)まで2次ベジエ曲線を描く。内部的に、Graphics.quadraticCurveTo()メソッドと同じ関数を参照する。ActionScriptユーザー向けに、同名のメソッドとして加えられた。
引数

Graphics.quadraticCurveTo()メソッドと同じ。
戻り値 メソッドが呼出されたGraphicsオブジェクト。

説明

Graphics.quadraticCurveTo()とGraphics.curveTo()メソッドは、Graphicsクラスの内部では同じ関数を参照し、オブジェクトに2次ベジエ曲線が描けます[*1]。ですから、以降はGraphics.quadraticCurveTo()メソッドで代表します。

Graphics.quadraticCurveTo()メソッドの描く「2次ベジエ」(Quadratic Bezier)は、始点と終点のふたつの座標に加えて、ひとつのコントロールポイントで曲線を定めます(図1左図)[*2]。Adobe Illustratorなどのベクターグラフィックスを描くアプリケーションでおなじみのベジエ曲線は、コントロールポイントがひとつ多い「3次ベジエ」(Cubic Bezier)です(図001右図)。3次ベジエ曲線を描くには、Graphics.bezierCurveTo()メソッドを用います。

図001■2次ベジエと3次ベジエの曲線のつくり
図001
*ActionScript 3.0コンポーネントリファレンスガイド「Graphics」の「curveTo()メソッド」の項より引用。

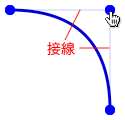
2次ベジエは、3次ベシエよりコントロールポイントがひとつ少ないため、プログラムで扱いやすくなります。けれど、3次ベジエのような細かな変化を曲線に加えることはできません(たとえば、次項の「例』でご説明するとおり、厳密な正円は描けません)。2次ベジエのコントロールポイントは、両端の座標から曲線の接線を延ばし、その交点に置きます(図002)。

図002■コントロールポイントと両端を結ぶ直線は曲線の接線になる
図002
>>jsdo.itシミュレーションサンプル

曲線を描くとき、線のカラーはGraphics.beginStroke()、線の太さなどのスタイルはGraphics.setStrokeStyle()メソッドで定めます。そして、Graphics.moveTo()メソッドで始点を決め、Graphics.quadraticCurveTo()メソッドの呼出しにより曲線が描かれます。

Graphicsオブジェクト.beginStroke(カラー);
Graphicsオブジェクト.setStrokeStyle(各スタイル, …);
Graphicsオブジェクト.moveTo(始点x座標, 始点y座標);
Graphicsオブジェクト.quadraticCurveTo(コントロールx座標, コントロールy座標, 終点x座標, 終点y座標);

Graphicsクラスのメソッドは、基本的に参照したGraphicsオブジェクトを返します。ですから、さらにドット(.)に続けて、つぎのメソッドが呼出せます。つまり、いくつものGraphicsクラスのメソッドの呼出しを、ひとつのステートメントに書き連ねることができるのです。

Graphicsオブジェクト.beginStroke(カラー)
.setStrokeStyle(各スタイル, …)
.moveTo(始点x座標, 始点y座標)
.quadraticCurveTo(コントロールx座標, コントロールy座標, 終点x座標, 終点y座標);

[*1] quadraticCurveTo()はCanvas、curveTo()はActionScriptの同じ名前のメソッドからそれぞれ名づけられたものと考えられます。

[*2] 2次ベジエ曲線の仕組みについては、Rui's Blog「中学生でもわかるベジェ曲線」や、てっく煮ブログ「ベジエ曲線の仕組み (2) - ２次ベジエ曲線を詳しく」が参考になるでしょう。

例

Graphics.quadraticCurveTo()メソッドから導かれる2次ベジエ曲線では、厳密な正円は描けません。けれども、正円をいくつかの扇形に等分して、それぞれの円弧に近い2次ベジエ曲線をつなぎ合わせれば、正円と見分けがつかないくらいの円形はつくれます。そこで、近似した円が描けるつぎのような関数を定めてみましょう。もちろん、EaselJSではGraphics.drawCircle()メソッドで簡単に正円はつくれます。この例は、Graphics.quadraticCurveTo()メソッドの使い方、とくにコントロールポイントの座標の求め方を練習するものです。

function xDrawCircle(Graphicsオブジェクト, 中心x座標, 中心y座標, 半径, 分割数)

関数の第1引数にはGraphicsオブジェクトを渡します。そして、線のカラーやスタイルの設定(Graphics.beginStroke()やGraphics.setStrokeStyle()メソッドの呼出し)はしません。好みの線の設定は済ませたGraphicsオブジェクトを渡して、円が描けるようにです。第2および第3引数で円の中心座標を定め、第4引数には円の半径を渡します。さらに、第5引数で、円を何等分して描くか、整数で与えられるようにしました。

そこで、この関数はたとえばつぎのように呼出します。サンプルのscript要素全体は、後にコード001としてまとめて掲げます。ステートメント頭の行番号はコード001にもとづきます。描画用のShapeインスタンスをつくり、Shape.graphicsプロパティからGraphicsオブジェクトを取出します(第9〜10行目)。そして、Graphicsオブジェクトに線のカラーと太さを定めたうえで、関数にそのオブジェクトを渡して呼出しています(第11〜13行目)。

  1. var drawShape = new createjs.Shape();
  2. var drawGraphics = drawShape.graphics;
  3. drawGraphics.beginStroke("blue")
  4. .setStrokeStyle(2);
  5. xDrawCircle(drawGraphics, centerX, centerY, 50, 8);

Graphics.quadraticCurveTo()メソッドで近似した正円を描く関数は、つぎのように定めます。第4引数の分割数(nSegments)から、扇形ひとつ当たりの中心角(nAngle)を求めます(第19行目)。三角関数を使うため、単位はラジアンにします(360度 = 2πラジアン)。そして、円はx軸の正、つまり3時方向から描き始めます(第20行目)。

  1. function xDrawCircle(myGraphics, nX, nY, nR, nSegments) {
  1.   var nAngle = 2 * Math.PI / nSegments;   // 分割した角度(ラジアン)
  2.   myGraphics.moveTo(nX + nR, nY);
  3.   for (var i = 1; i<= nSegments; i++) {   // 指定数に分割して弧を描画
  4.     var nTheta = i * nAngle;   // 回転角(ラジアン)
        // アンカーポイントの座標
  5.     var nAnchorX = nR * Math.cos(nTheta);
  6.     var nAnchorY = nR * Math.sin(nTheta);
        // コントロールポイントの座標
  7.     var nControlX =
        nAnchorX + nR * Math.tan(nAngle / 2) * Math.cos(nTheta - Math.PI / 2);
  8.     var nControlY =
        nAnchorY + nR * Math.tan(nAngle / 2) * Math.sin(nTheta - Math.PI/2);
        // 弧の描画
  9.     myGraphics.quadraticCurveTo(nControlX + nX, nControlY + nY, nAnchorX + nX, nAnchorY + nY);
  10.   }
  11. }

繰返しのforステートメントの中身が本題です(第21〜30行目)。先ほど求めた中心角(nAngle)を順に増やした角度(nTheta)にもとづき(第22行目)、曲線を描く先の座標(nAnchorX, nAnchorY)とコントロールポイント(nControlX, nControlY)を計算したうえで(第23〜28行目)、Graphics.quadraticCurveTo()メソッドにそれらの座標値を渡して呼出しています(第29行目)。

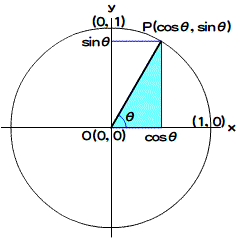
曲線を描く先の座標(nAnchorX, nAnchorY)とコントロールポイント(nControlX, nControlY)の導き方について、もう少し細かくご説明しましょう。そのとき、三角関数のsinとcosを用います。原点O(0, 0)を中心とする半径1の円(これを「単位円」と呼びます)において、円周上の点Pの座標は、OPがx軸となす角をθとすると、つぎの式で表されます(図003)。詳しくは、「角度を座標にする三角関数sinとcos」(PDF)をお読みください。

x = cosθ
y = sinθ

図003■単位円上の点がx軸となす角をθとすると座標は(cosθ, sinθ)
図003

このsinとcosの定義より、原点(0, 0)からの距離がr、x軸とθの角度なす座標(x, y)はつぎの式で示されます。つまり、原点からの距離およびx軸となす角度がわかれば、その座標が求まるということです。

x = r cosθ
y = r sinθ

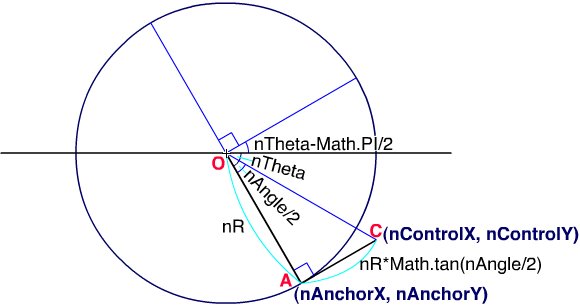
改めて、曲線を描く先の座標(nAnchorX, nAnchorY)とコントロールポイント(nControlX, nControlY)の求め方に戻ります。わかりやすいように、円の中心を原点(0, 0)に定めたのが、つぎの図004です。3時の方向から時計回りに中心角(nAngle)の倍数で増やす角度(nTheta)に対して、曲線を描く先の座標(nAnchorX, nAnchorY)がA、コントロールポイント(nControlX, nControlY)をCとしています。

図004■曲線を描く先の座標とコントロールポイントを求める
図004

曲線を描く先(A)の座標
OAの長さは円の半径nR、OAがx軸となす角はnThetaです。すると、曲線を描く先Aの座標(nAnchorX, nAnchorY)は、前述sinとcosの定義よりつぎの式で示されます。三角関数のsinとcosは、それぞれMath.sin()およびMath.sin()メソッドで得られます。

  1. var nAnchorX = nR * Math.cos(nTheta)
  2. var nAnchorY = nR * Math.sin(nTheta)

コントロールポイント(C)の座標
先に、Aから見たCの座標(Δx, Δy)を求めることにします。つまり、原点をAに定めたときの、Cの座標です。ACがx軸となす角度をθとすると、やはりsinとcosの定義から、つぎの式が導かれます。なお、OA⊥ACですので、θはnThetaを時計と逆方向に90度(π/2ラジアン)回した角度に等しく、θ = nTheta - π/2です。

Δx = AC cosθ
Δy = AC sinθ

つぎに、ACの長さを求めます。角Aを直角とする直角三角形OACにおいて、∠AOCをφとすると、tanφ = AC / OA(= sinφ / cosφ)で定義されます。すると、ACの長さはつぎの式で示されます。

AC = OA tanφ

このACの値を、前記Aから見たCの座標(Δx, Δy)の式に代入します。

Δx = AC cosθ = OA tanφ cosθ
Δy = AC sinθ = OA tanφ sinθ

コントロールポイントは扇形の中心角の二等分線上に置きます。すると、φ = nAngle / 2です(前掲図004)。また、前述のとおり、OA = nR、θ = nTheta - π/2ですので、Aから見たCの座標(Δx, Δy)はつぎの式で表せます。

Δx = nR * Math.tan(nAngle / 2) * Math.cos(nTheta - Math.PI / 2)
Δy = nR * Math.tan(nAngle / 2) * Math.sin(nTheta - Math.PI / 2)

この座標値(Δx, Δy)をAの座標(nAnchorX, nAnchorY)にそれぞれ加えれば、コントロールポイントの座標(nControlX, nControlY)が求まります[*3]。

  1.     var nControlX =
        nAnchorX + nR * Math.tan(nAngle / 2) * Math.cos(nTheta - Math.PI / 2);
  2.     var nControlY =
        nAnchorY + nR * Math.tan(nAngle / 2) * Math.sin(nTheta - Math.PI/2);

2次ベジエ曲線を描く
曲線を描く先(A)とコントロールポイント(C)の座標がそれぞれ得られたら、Graphics.quadraticCurveTo()メソッドの引数に渡して2次ベジエ曲線を描きます。ただし、実際には円の中心は原点O(0, 0)ではなく、関数(xDrawCircle())が第2および第3引数に受取ったxy座標値(nX, nY)です。この中心座標は、Graphics.quadraticCurveTo()メソッドに渡す引数値にそれぞれ加えればよいのです。

  1.     myGraphics.quadraticCurveTo(nControlX + nX, nControlY + nY, nAnchorX + nX, nAnchorY + nY);

script要素全体を、以下のコード001にまとめて掲げました。ひとつつけ加えたのは、関数(xDrawCircle())の第5引数(nSegments)にデフォルト値を設けたことです。第5引数が渡されなかったら、引数にデフォルト値(8)を与えます(第18行目)。そこで、この関数を呼出すとき、第5引数は省きました(第13行目)。なお、論理和演算子||を用いたデフォルト値の代入については、「論理演算子を使った条件判定」をお読みください。

コード001■Graphics.quadraticCurveTo()メソッドで近似した正円を描く関数の定義
  1. <script src="http://code.createjs.com/easeljs-0.6.1.min.js"></script>
  2. <script>
  3. var stage;
  4. function initialize() {
  5.   var canvasElement = document.getElementById("myCanvas");
  6.   stage = new createjs.Stage(canvasElement);
  7.   var centerX = canvasElement.width / 2;
  8.   var centerY = canvasElement.height / 2;
  9.   var drawShape = new createjs.Shape();
  10.   var drawGraphics = drawShape.graphics;
  11.   drawGraphics.beginStroke("blue")
  12.   .setStrokeStyle(2);
  13.   xDrawCircle(drawGraphics, centerX, centerY, 50);
  14.   stage.addChild(drawShape);
  15.   stage.update();
  16. }
  17. function xDrawCircle(myGraphics, nX, nY, nR, nSegments) {
  18.   nSegments = nSegments || 8;
  19.   var nAngle = 2 * Math.PI / nSegments;
  20.   myGraphics.moveTo(nX + nR, nY);
  21.   for (var i = 1; i<= nSegments; i++) {
  22.     var nTheta = i * nAngle;
  23.     var nAnchorX = nR * Math.cos(nTheta);
  24.     var nAnchorY = nR * Math.sin(nTheta);
  25.     var nControlX =
        nAnchorX + nR * Math.tan(nAngle / 2) * Math.cos(nTheta - Math.PI / 2);
  26.     var nControlY =
        nAnchorY + nR * Math.tan(nAngle / 2) * Math.sin(nTheta - Math.PI/2);
  27.     myGraphics.quadraticCurveTo(nControlX + nX, nControlY + nY, nAnchorX + nX, nAnchorY + nY);
  28.   }
  29. }
  30. </script>

関数(xDrawCircle())の第5引数(nSegments)のデフォルト値を8としたことからも想像できるとおり、円は8分割もすれば正円との違いはほとんどわかりません。分割数によって見た目がどう変わるか、シミュレーションのコードをjsdo.itに掲げましたので、興味ある方はお試しください。3から12分割まで選べます。


[*3] 扇形はすべて同じかたちで、もちろん中心角(nAngle)も等しいです。つまり、ACの長さ(OA tanφ)はすべての扇形について同値になります。すると、forステートメントで毎回計算するのは無駄でしょう。けれど、定義した関数(xDrawCircle())は使い回すつもりはなく、ただの計算練習ですので、わかりやすいように式の中に含めました。

作成者: 野中文雄
更新日: 2013年6月25日 Graphics.setStrokeStyle()メソッドの引数に説明を追加。
作成日: 2013年6月24日

Copyright © 2001-2013 Fumio Nonaka.  All rights reserved.