サイトトップ
Director Flash 書籍 業務内容 プロフィール

Optimizing Performance of ActionScript 3.0

Chapter 04 数値の演算

□04-03 距離はPointやVector3DクラスのメソッドよりMath.sqrt()で三平方の定理を使う

PointやVector3Dクラスには、座標と座標の間の距離を求める同じ名前の静的メソッドdistance()があります。しかし、速さを稼ぐにはこれらのメソッドでなく、Math.sqrt()メソッドを用いて三平方の定理で導く方がお得です。また、このとき各座標値を2乗するのは、Math.pow()メソッドより、単純に変数に入れた座標値を2回掛合わせましょう。

    【座標間の距離を求める】
  1. 座標間の距離はMath.sqrt()メソッドを用いて三平方の定理で計算する
  2. 数値の2乗はMath.pow()メソッドより同じ変数を2回掛けた方が速い

○04-03-01 Point.distance()とVector3D.distance()メソッド
Point.distance()とVector3D.distance()は、ともに座標と座標の間の距離を求める静的メソッドです。引数には、座標が納められたPointまたはVector3Dインスタンスをふたつ渡します。たとえば、2次元平面上のふたつの座標(1, 1)と(2, 1 + √3)との間の距離は、PointオブジェクトとPoint.distance()を使ってつぎのスクリプト04-03-001のように求めます。

スクリプト04-03-001【○】2次元平面上の2点間の距離をPoint.distance()メソッドで求める
  1. var begin:Point = new Point(1, 1);
  2. var end:Point = new Point(2, 1 + Math.sqrt(3));
  3. var distance:Number = Point.distance(begin, end);
  4. trace(distance);   // 出力: 1.9999999999999998

2点間の距離は、正確には2になります。[ムービープレビュー]で[出力]を見ると、計算にはわずかな誤差が含まれているようです。

Vector3D.distance()は、z座標が加わったVector3Dオブジェクトを使うだけで、メソッドの呼出し方は変わりません。座標(1, 1, 1)と(2, 1 + √3, 1)の間の距離は、つぎのスクリプト04-03-002で求まります。ふたつの点のz座標値が同じですので、上記スクリプト04-03-001と同じく距離は2になります。

スクリプト04-03-002【○】3次元空間上の2点間の距離をVector3D.distance()メソッドで求める
  1. var begin:Vector3D = new Vector3D(1, 1, 1);
  2. var end:Vector3D = new Vector3D(2, 1 + Math.sqrt(3), 1);
  3. var distance:Number = Vector3D.distance(begin, end);
  4. trace(distance);   // 出力: 1.9999999999999998

これらのメソッドを、決して使っていけないという訳ではありません。ただ、座標は大量に扱うことがめずらしくなく、計算の速さを求めなければならない場合があります。そのようなとき、2点間の距離を求めるのに、Math.sqrt()メソッドで三平方の定理により導くのが有効だということです。


○04-03-02 三平方の定理で2点間の距離を求める
三平方の定理について、簡単におさらいします。すでにおわかりの読者は、この項は飛ばして構いません。

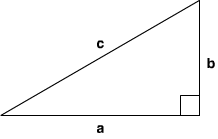
直角三角形の直角を挟んだ2辺の長さをそれぞれaとb、直角に対する斜辺(もっとも長い辺)の長さをcとすると(図04-03-001)、つぎの等式が成立ちます。これを「三平方の定理」あるいは「ピタゴラスの定理」と呼びます。

a2 + b2 = c2

図04-03-001■三平方の定理
a2 + b2 = c2
直角を挟んだ2辺の長さをaとb、斜辺の長さをcとする。

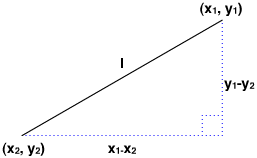
三平方の定理を使うと、2点間の距離を求めることができます。2次元平面上の2点の座標をそれぞれ(x1, y1)および(x2, y2)とし、2点間を結ぶ直線を斜辺とした直角二等辺三角形を考えます(図04-03-002)。すると、直角二等辺三角形の底辺がx1 - x2、高さはy1 - y2になります。よって、2点間の長さをlとしたとき、三平方の定理より、つぎの等式が成立ちます。

l2 = (x1 - x2)2 + (y1 - y2)2
  ________________
l = √ (x1 - x2)2 + (y1 - y2)2
図04-03-002■2次元平面上の2点間の距離を三平方の定理で求める

直角を挟む2辺はそれぞれx1 - x2とy1 - y2になる。

Tips 04-03-001■距離は0以上の数値
三平方の定理で立てた方程式から両辺の平方根を求めると、方程式そのものの解は正負のふたつが得られます。

l2 = (x1 - x2)2 + (y1 - y2)2
  ________________
l = ±√ (x1 - x2)2 + (y1 - y2)2

しかし、求める2点間の距離は0以上で定められますので、本文のとおり正数が解となります。ちなみに「なぜならば」は、数学記号「∵」で表します。

  ________________
l = √ (x1 - x2)2 + (y1 - y2)2   (∵ l≧0)

3次元空間ではz座標が加わります。2点の座標をそれぞれ(x1, y1, z1)および(x2, y2, z2)とした場合も、同じように三平方の定理から距離lがつぎの式で導かれます。

  _________________________
l = √ (x1 - x2)2 + (y1 - y2)2 + (z1 - z2)2

Tips 04-03-002■3次元空間における2点間の距離
3次元空間でふたつの座標の間の距離を求めるには、三平方の定理を2度使います(図04-03-003)。

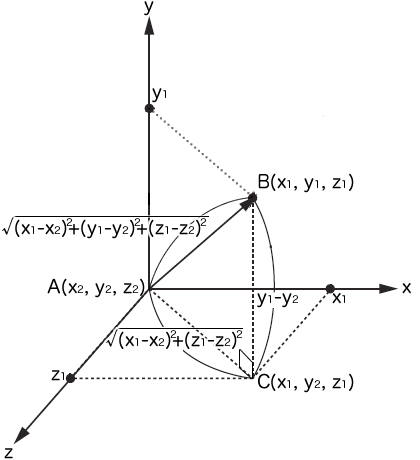
図04-03-003■3次元空間の2点間の距離を三平方の定理で求める

点A(x2, y2, z2)を通ってy軸と垂直な平面に対して、点B(x1, y1, z1)から垂線を下ろし、点Cとする。

まず、点A(x2, y2, z2)を通ってy軸と垂直な平面に対して、点B(x1, y1, z1)から垂線を下ろします。すると、その垂線と平面との交点Cは、座標が(x1, y2, z1)になります。点Cは点Aとy座標値が同じですので、z軸とx軸からなる2次元平面と捉えて、前述の三平方の定理からつぎのようにACの距離が求まります。

  ________________
AC = √ (x1 - x2)2 + (z1 - z2)2

つぎに、三角形ABCは直角三角形ですので、ACとBC(= y1 - y2)から三平方の定理を使ってABが導けます。

AB2 = AC2 + BC2
    ________________  
= (√ (x1 - x2)2 + (z1 - z2)2 )2 + (y1 - y2)2
= (x1 - x2)2 + (z1 - z2)2 + (y1 - y2)2
    _________________________
AB = √ (x1 - x2)2 + (y1 - y2)2 + (z1 - z2)2

○04-03-03 クラスの静的メソッドと同じ仕様で2点間の距離を返す関数の定義
それでは、Math.sqrt()メソッドと三平方の定理により2点間の距離を導くスクリプトについて考えましょう。ふたつのクラスの静的メソッドPoint.distance()とVector3D.distance()と同じ仕様で関数を定めます。

まず。以下のスクリプト04-03-003が、Point.distance()メソッドと同じく、引数として渡したふたつのPointオブジェクトからその間の距離を求めて、Number型で返す関数distance2D()です。引数のPointインスタンスからxy座標をそれぞれ取出して、三平方の定理により距離を求めて返しています。なお、xy各座標の差をそれぞれ2乗するとき、変数に入れた差を単純に2回掛合わせています(第4行目)。この計算の方がMath.pow()メソッドを使うよりも速く、見た目がわかりにくいということもないからです。

Point.distance()メソッドを使った前掲スクリプト04-03-001と同じ座標値で試すと、誤差までまったく同じ値が返されます。

var begin:Point = new Point(1, 1);
var end:Point = new Point(2, 1 + Math.sqrt(3));
var distance:Number = distance2D(begin, end);
trace(distance);   // 出力: 1.9999999999999998

スクリプト04-03-003【◎】2次元平面の2点間の距離を引数のふたつのPointオブジェクトから求めて返す
  1. function distance2D(beginPoint:Point, endPoint:Point):Number {
  2.   var nX:Number = endPoint.x - beginPoint.x;
  3.   var nY:Number = endPoint.y - beginPoint.y;
  4.   var distance:Number = Math.sqrt(nX * nX + nY * nY);
  5.   return distance;
  6. }

つぎに、以下のスクリプト04-03-004が、Vector3D.distance()メソッドと同じ仕様の関数distance3D()を定めます。Pointクラスにもとづく前掲スクリプト04-03-003のクラスをVector3Dに替え、z座標値の計算を加えただけです。

こちらもVector3D.distance()メソッドを用いた前掲スクリプト04-03-002と同じ座標値で試せば、戻り値はまったく同じです。

var begin:Vector3D = new Vector3D(1, 1, 1);
var end:Vector3D = new Vector3D(2, 1 + Math.sqrt(3), 1);
var distance:Number = distance3D(begin, end);
trace(distance);   // 出力: 1.9999999999999998

スクリプト04-03-004【◎】3次元空間の2点間の距離を引数のふたつのVector3Dオブジェクトから求めて返す
  1. function distance3D(beginVector3D:Vector3D, endVector3D:Vector3D):Number {
  2.   var nX:Number = endVector3D.x - beginVector3D.x;
  3.   var nY:Number = endVector3D.y - beginVector3D.y;
  4.   var nZ:Number = endVector3D.z - beginVector3D.z;
  5.   var distance:Number = Math.sqrt(nX * nX + nY * nY + nZ * nZ);
  6.   return distance;
  7. }

[*筆者用参考]

「距離はPointやVector3DクラスのメソッドよりMath.sqrt()と三平方の定理で求める方が速い」

@k5n6「指数が整数であっても、不定な指数で累乗を求めるならば、Math.powは意外と速い」

Point.distance - wonderfl build flash online

作成者: 野中文雄
作成日: 2011年4月23日

Copyright © 2001-2011 Fumio Nonaka.  All rights reserved.