●解説
平面上にxy座標が(cosθ, sinθ)の点を取り、角度θの値を増減させると、点は原点から半径1の円周上を移動します。つまり、角度θを変数として、座標(cosθ, sinθ)の位置を計算すれば、円運動がシミュレートできることになります。ここで使う三角関数のメソッドMath.cos()およびMath.sin()の説明は、前項「バネや波の動きをシミュレートしたい」をご覧ください。
→関連項目
「バネや波の動きをシミュレートしたい」
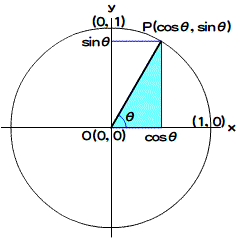
図01-04-001■sinとcosの値の角度に対する変化【FigMath03-002.png】
|
※sinとcosの定義
座標(cosθ, sinθ)が半径1の円周上の点であることは、三角関数sinおよびcosの定義です。つまり、角度θに対する半径1の円周上の座標(x, y)を計算し、xはcosθ、yがsinθと定義されました。おそらく高校で習った三角比による定義(図01-04-002)は、その計算の仕方です。ただし、三角比では、θが90度(π/2ラジアン)以上のときは別に考えなければなりません。
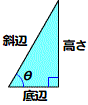
図01-04-002■三角比によるsinおよびcos【FigMath03-003.png】
|
sinθ = 高さ/斜辺
cosθ = 底辺/斜辺
|
 |
|
座標(cosθ, sinθ)は半径1の円周上を動きます。半径をもっと大きくしたい場合には、その値を比例係数としてxy座標値に乗じます。また、円起動の中心点は原点(0, 0)です。この位置を動かすには、その値を各座標に加えればよいでしょう。したがって、中心座標が(a, b)で半径rの円の方程式は、つぎのように表されます。
|
x = a + r cosθ
y = b + r sinθ
|
さらに、三角関数値に比例係数として掛合わせる半径の値をx座標とy座標とで異なる値にすれば、垂直方向と水平方向の大きさの比率が変わり、楕円の方程式になります。
|
x = a + rx cosθ
y = b + ry sinθ
|
○記述例
以下のスクリプト01-04-001をMovieClipシンボルのフレームアクションに設定すると、インスタンスがステージを中心に楕円軌道で回転します(図01-04-003)。楕円の半径は、水平方向に100ピクセル、垂直方向は50ピクセルで指定しています。DisplayObject.enterFrameイベント(定数Event.ENTER_FRAME)のリスナー関数xRotate()では、一定に増加する角度に対して楕円の方程式によりyx座標を計算して、インスタンスのDisplayObject.xおよびDisplayObject.yプロパティに設定しています。
スクリプト01-04-001■インスタンスを楕円軌道で回転させる
|
// フレームアクション
// MovieClip: 楕円軌道で回るインスタンス
var nRadian:Number = 0;
var nIncrement:Number = 0.1;
var nRadiusX:Number = 100;
var nRadiusY:Number = 50;
var nX:Number = stage.stageWidth / 2;
var nY:Number = stage.stageHeight / 2;
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
x = nX + nRadiusX * Math.cos(nRadian);
y = nY + nRadiusY * Math.sin(nRadian);
nRadian += nIncrement;
nRadian %= 2*Math.PI;
}
|
なお、リスナー関数xRotate()の最後のステートメントで剰余後代入演算子%=で2πの剰余を取っている理由は、前出「バネや波の動きをシミュレートしたい」の「※周期的な演算で変数値の範囲を限定する」をお読みください。
図01-04-003■インスタンスがステージ中心から描く楕円軌道で回転【ActionScript30_07_007.png】

作成者: 野中文雄
ドラフト作成: 2009年5月12日