ハンズオン講座:
2018年02月09日金曜日「Vue.js入門講座」
2018年02月23日金曜日「jQueryではじめるJavaScript入門」
■Twitter: @FumioNonaka / Facebook Page: CreateJS
Creators MeetUp vol.22
sinとcosは何する関数?
三角関数のsinとcosは、直角三角形の辺の比率として初めに習う。それをプログラムのアニメーション表現で使うのは、おもに円運動だ。「三角」がどうして「円」になるのか、疑問をもったとしても不思議はない。sinとcosはどう定められ、どういう性質があるのかという基本を中心に、変わったアニメーションの応用表現も紹介したい。
このレジュメは、2014年11月15日土曜日に催された第22回Creators Meetupで務めた高座「sinとcosは何する関数?」向けとして書いた。当日のYouTube録画をつぎに掲げる。
01 三角関数のsinとcosの求め方と性質
三角関数は、高校数学で初めに直角三角形を用いた三角比で習う(図001)。sinとcosは、直角三角形の高さと底辺それぞれの斜辺に対する比だ。といわれて、素直に納得はしづらい。
図001■三角関数は初め三角比で習う

*ビジュアル数学「三角比・三角関数」より引用。
プログラムのアニメーション表現では、円運動で使われる(図002)。式をそのまま写しさえすれば、確かに円周上を回る。
図002■xy座標を(cosθ, sinθ)で定めると円運動が表せる
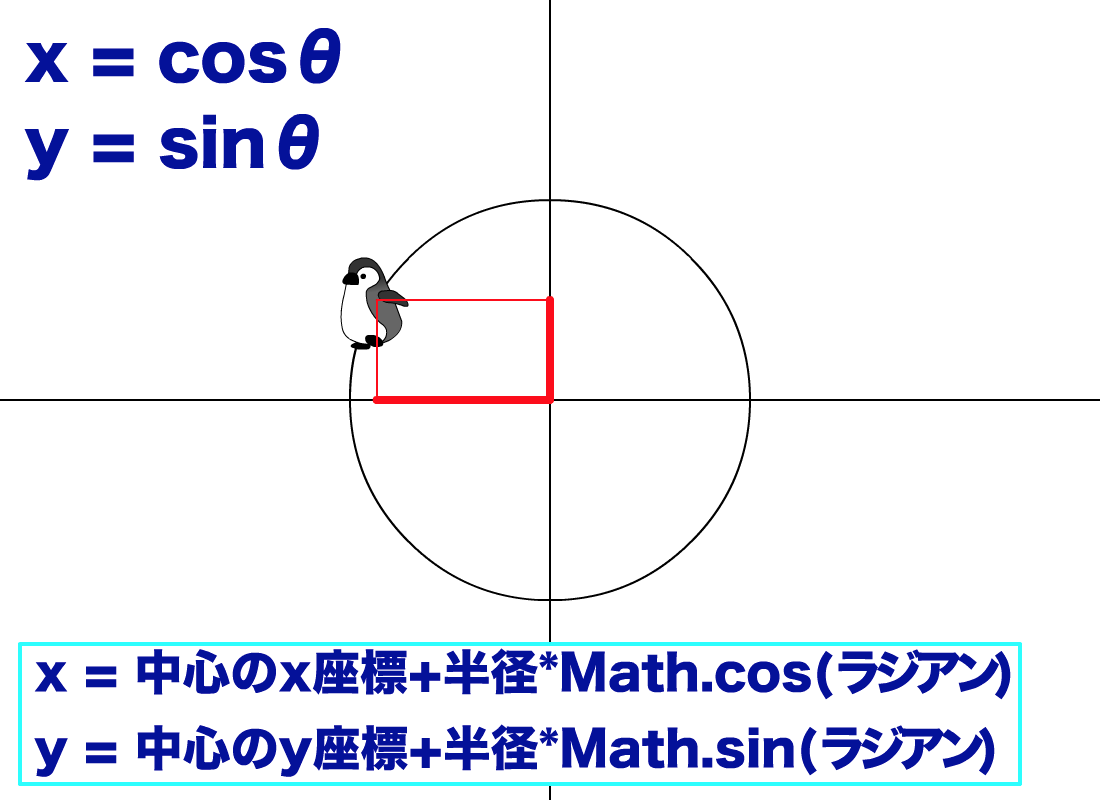
*上図をクリックすると、サンプルSWFが開く。
でも、
「三角」なのに、なぜ「円」運動?
加えて、三角関数の公式は数が多くて、直感的にわかりにくい。
sin2θ + cos2θ = 1
sin(θ±φ)=sinθcosφ±cosθsinφ
a2 = b2 + c2 - 2bc cosθ
…
02 理解すれば覚えることは減る
三角関数はとっつきにくいと感じられやすい。理由はいくつか考えられる。
- ギリシャ文字「θ」が嫌
- 覚えることが多い
- 使い途がわからない
理解の順番を間違えると、覚えることばかりになる。三角関数は、そもそも半径1の円(「単位円」)の円周上の座標として定められている(図003)。三角比でなく、こちらが定義になる。また、直角三角形に三平方の定理を当てはめたのがつぎの式だ。
sin2θ + cos2θ = 1
図003■半径1の円周上のxy座標が角度θに対して(cosθ, sinθ)と定められた
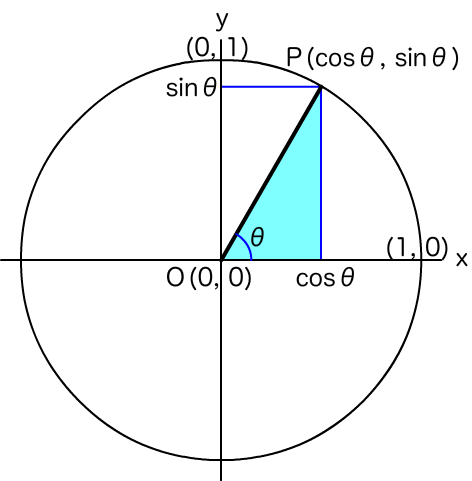
だから、角度を変えれば座標は定義にしたがって円周上を動く(図004)。つまり、そういうふうにできている。
図004■角度を変えれば座標は円周上を動く
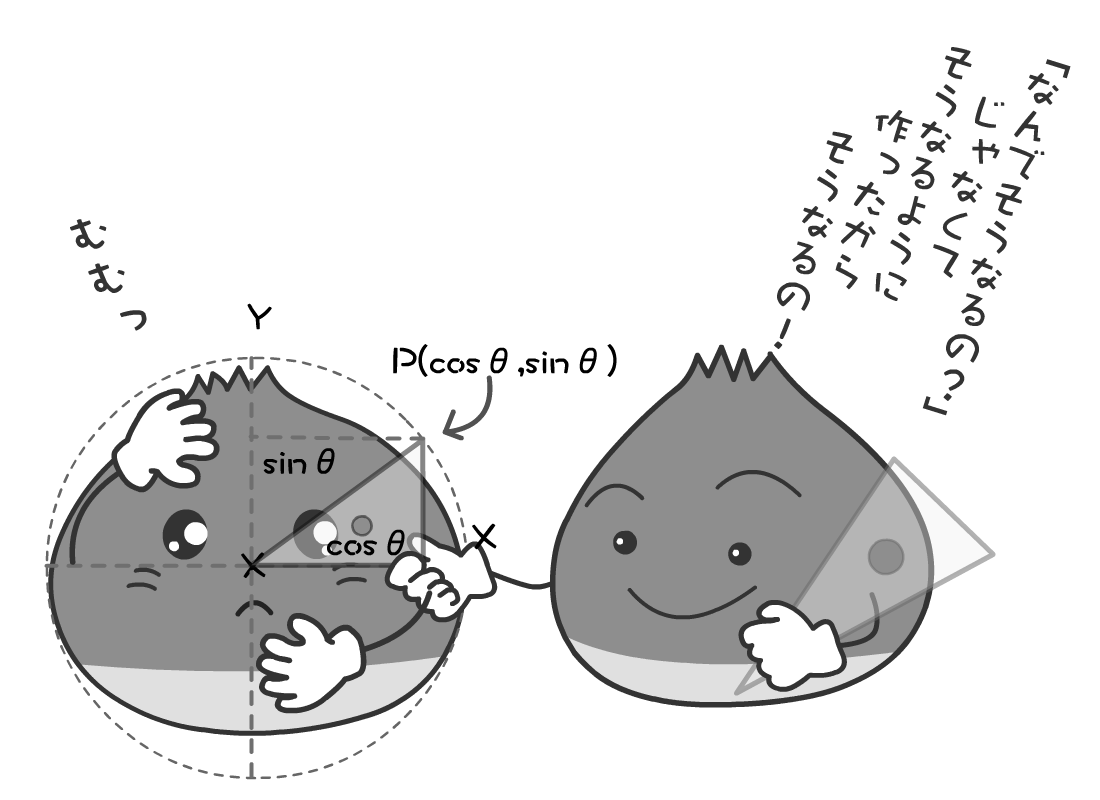
三角比も、単位円にもとづく三角関数の定義から直ちに求まる。cosとsinは半径1のときのxy座標なのだから、底辺(x)と高さ(y)をそれぞれ斜辺(r)で割ればよい(図005)。逆に、半径(r)と角度(θ)が与えられたときのxy座標P(r cosθ, r sinθ)を示す場合の方が多い。
図005■xy座標を半径で割ればcosとsinが求まる
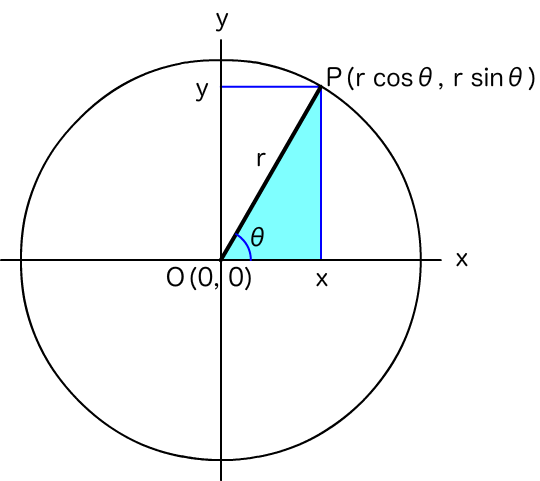
-
sinθ = y / r
cosθ = x / r
そして、三角関数の余弦定理と三平方の定理の間には隠れた関係が!(証明は「余弦定理」参照)
sinやcosを用いたアニメーション表現としては、ほかにバネや波の動きがある(図006)。垂直方向にsinで座標を変えれば、バネの縦の振動だ。さらに、水平方向には等速度で動かすと波になる。
図006■sinやcosはバネや波の動きを表す
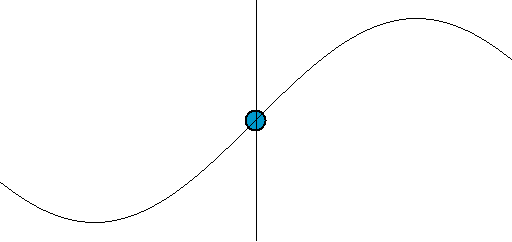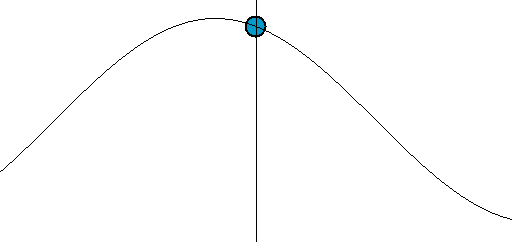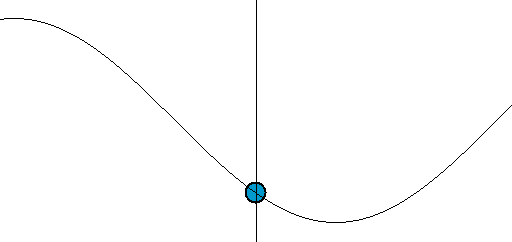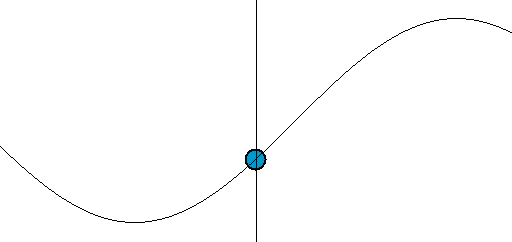
*Wikipedia「Harmonic oscillator」より引用。
03 スピログラフを回してみる
穴の空いた大きな定円の中で、歯車のような小さな動円を回しながら、動円の描画点の穴から筆記用具の先を通して幾何学模様を描く(図007)。スピログラフを使って描かれたアートもある。
スピログラフ(英: Spirograph)は、曲線による幾何学模様を描くための定規の一種である。主に玩具店で販売されていることから玩具ともみなされている。「スピログラフ」 という名称はハズブロの登録商標である。
*Wikipedia「スピログラフ」より引用。
図007■Spirograph スピログラフ
描かれる曲線は「ハイポトロコイド」(Hypotrochoid)と呼ばれ、つぎの方程式で表される。
定円の半径をrc、動円の半径はrm、そして動円の中心から描画点までの距離をrdとする。
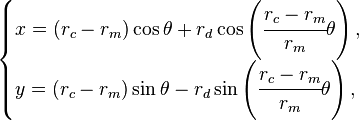
図008■ハイポトロコイド

応用例としてサンプル001は、曲線そのものを描くのではなく、その上の2点を一定間隔で直線により結んだ。さらに、パラメータに現在時刻のミリ秒を含めたため、グラフィックスは時々刻々変わる。
サンプル001■Using trochoid to draw lines
参考: fladdict「標本002 三角関数」
作成者: 野中文雄
更新日: 2018年1月19日 リンク切れは補正し、体裁を整えた。
作成日: 2014年11月14日
Copyright © 2001-2018 Fumio Nonaka. All rights reserved.

