ビデオライブラリ:
LinkedInラーニング
ハンズオン講座:
「jQueryではじめるJavaScript入門」
「Vue.js入門講座」

■Twitter: @FumioNonaka / Facebook Page: CreateJS / Away3D

Creators MeetUp vol.30

ネイピア数〜美しきムダな数〜

「ネイピア数」eは、自然対数の底として用いられ、多くのプログラミング言語に定数Math.Eとして備わる。けれど、ほとんどの人生にまったく必要のない数で、この定数を使わずに過ごすプログラマが大半だろう。これほどまでに実用性のとぼしい定数が、数学や自然界のふとした端々に顔を現す。そんな「ネイピア数」の生態を追ってみたい。

このレジュメは、2015年7月18日土曜日に催された第30回Creators Meetupで務めた同名の高座の参加者向けとして書いた。当日のYouTube録画をつぎに掲げる。

00 明日も使えないムダ知識

01 ネイピア数の由来

自然対数の底eの呼び名「ネイピア数」の由来はジョン・ネイピア(John Napier)。対数の発見者として知られる(図001)。

図001■ジョン・ネイピア

引用: Wikipedia「ジョン・ネイピア」

明日も使えぬムダ知識 01

「ネピア」(nepia)のブランド名の由来となった王子製紙がニュージーランドに進出した町の名前は、ジョン・ネイピアと同じ「Napier」だった。

02 ネイピア数を求める

ネイピア数を見い出したのはヤコブ・ベルヌーイだとされる。複利計算の過程でこの定数の重要性に気づいた。

明日も使えぬムダ知識 02

「ネイピア数」の名前の由来となったジョン・ネイピアは、実はネイピア数を発見していなかった。

03 100分の1を100回やってみる

「100回試したら一度は起こって欲しい事象に1/100の確率を使う馬鹿多過ぎｗこれを100人で試したら、36人は統計的に100回では起きない概算になる。」(遠藤雅伸@evezoo)

乱数は、意図した演出の範囲から逸脱しない誤差の揺らぎに使うべき。100回試したら一度は起こって欲しい事象に1/100の確率を使う馬鹿多過ぎｗこれを100人で試したら、36人は統計的に100回では起きない概算になる。
— 遠藤雅伸 (@evezoo) 2010年11月10日

参考: ゲームの神様「100分の1を100回やってみる」

たとえば、100個にひとつ当たりが入っているチョコレートを箱買いした場合と、100個に1個の割合で当たり玉の入った福引の場合の違い。

図002■福引の「ガラポン」

1/nの確率でn回試しても事象が起きない確率を計算してみた。

上記リンクの中でm = n - 1と置いたとき、式は厳密にはつぎのように変形される。

(1 - 1/n)ⁿ = {1 / (1 + 1/m)}^m+1
= {1 / (1 + 1/m)}^m{1 / (1 + 1/m)}

nを無限大にすればmも無限大になり、前項は1/eに、後項は1に収束する。したがって、極限値は(1/e)×1 = 1/eとなる。

04 ベルヌーイの螺旋

「ベルヌーイの螺旋」(対数螺旋)は、極座標表示(r, θ)で

r = e^θ

により描かれる(図003)。

図003■対数螺旋

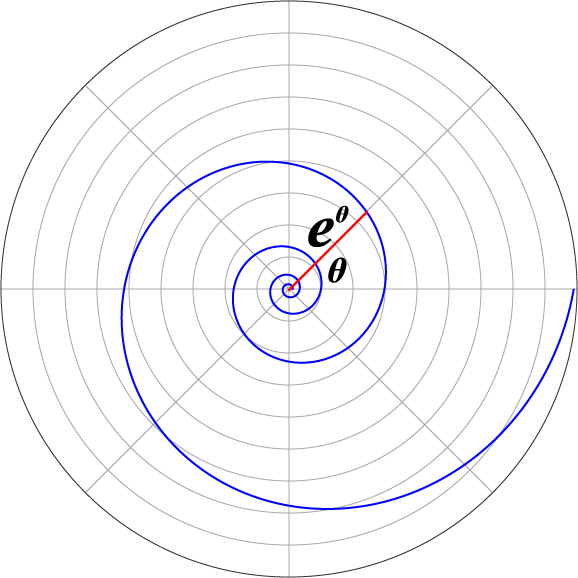
引用: Wikipedia「対数螺旋」

一般には、螺旋の広がる大きさ(a)と曲がり具合(b)を調整する係数が加えられ、つぎの式で表される(Wikipedia「対数螺旋」)。

r = ae^bθ

自然界にも見られ、建造物に採り入れられた例もある。拡大・縮小してもかたちが変わらない(図004)。

図004■拡大・縮小してもかたちが変わらない

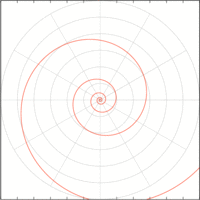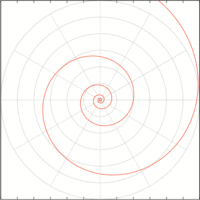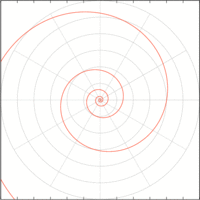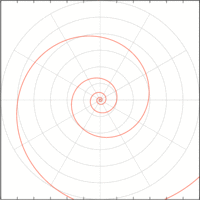
引用: Wikipedia「対数螺旋」

数学的には、原点と螺旋上の任意の点を結んだとき、その線分と接線の角度が一定になる(図005)。はやぶさが獲物に近づくとき、対数螺旋を描いて飛ぶ(Wikipedia「対数螺旋」の「自然界における対数螺旋」)。

ハヤブサは獲物まで最短距離で飛ばず、対数螺旋の経路をたどる。ハヤブサの目は頭の両側にあるため、獲物を一定の角度で捉えながら飛行すると、図のように自然と対数螺旋飛行になる。（『黄金比はすべてを美しくするか？』より） pic.twitter.com/hlC3np98QM
— 風霊守 (@fffw2) 2014年7月27日

図005■原点と螺旋を結ぶ線分とその点の接線の角度はつねに一定

引用:「logarithmic spiral」

ベルヌーイの望みは Eadem mutata resurgo(変化しても同じように生まれ変わる)の語句とともに、墓石にこの螺旋を彫ってもらうことであった(Wikipedia「対数螺旋」の「歴史」)。

明日も使えぬムダ知識 03

ベルヌーイは自分の墓石にベルヌーイの螺旋を刻んでほしいと願ったが、間違ってアルキメデスの螺旋が彫られてしまった。

図006■アルキメデスの螺旋

05 オイラーの等式

【オイラーの公式】
e^iθ = cosθ + i sinθ

特別な場合としてθ = πを代入する。

【オイラーの等式】
e^iπ + 1= 0

e : ネイピア数。自然対数の底。微分積分学で広く出現。
i : 複素数における虚数単位。積分などにおいてより深い洞察に導く。
1 : 乗法の単位元
0 : 加法の単位元。
π : 円周率。三角比、ユークリッド幾何学、微分積分学で頻出。

数学的な美を示す。「なにも足さないなにも引かない」。

全世界の数学者が感動した!!
ベンジャミン・パース(19世紀ハーバード大学数学教授)のことば

[2018年6月2日: 追記]

appendix 秘書問題

解にネイピア数eが表れる興味深い問題に「秘書問題」がある。解説は「秘書問題 – 結婚相手や恋人はこうやって選ぶのがベスト！」がわかりやすい。

作成者: 野中文雄
更新日: 2018年6月2日レイアウトを整え、画像の挿入など若干の補正を加えた。また参考として、appendix「秘書問題」を追加。
作成日: 2015年7月19日