LinkedInラーニング
ビデオライブラリー
Vue.js入門
JavaScript基本講座
■Twitter: @FumioNonaka / Facebook Page: CreateJS

Creators MeetUp vol.41

統計と確率の見方・考え方

このレジュメは、2016年6月25日土曜日開催の第41回Creators Meetupで務めた同名の高座のまとめになる。数式は使わずに、統計と確率の考え方について説明した。また、当日のYouTube録画を併せて掲げる。なお、以下のTEDの公演では、学校の数学教育で統計と確率を学ぶ重要性が語られている。

参考: TED「アーサー・ベンジャミン：数学の教育を変えるための公式」

01 統計は相関関係を示す

Forbes「フェイスブックは『人生の幸福度を下げる』米研究結果」によると、「SNSの利用頻度が高いほど、うつ病になりやすい」という。だが、統計が基本的に示すのは因果関係でなく、相関関係でしかない。つまり、この研究結果から導かれることは、SNS利用頻度の多寡とうつ病リスクの高低の傾向が近いというだけだ。記事のタイトルは煽りで、SNSの利用頻度を原因としてうつ病を起こすという意味ではない。

「勉強部屋が広いほど成績がいい」という統計は(実際に採られていないけれど)有意な結果が得られると推測されている。もちろん、「部屋を広くすると成績が上がる」ということではない。勉強部屋が広いのは、以下のことを意味すると考えられる。

部屋が広いのは金持ち
子どもの教育に関心がある
教育に金をかける

他の条件が同じであれば、このような環境に育った子どもの成績が少しよくても不思議はない。統計はその解釈が重要だ。

02 学校の成績と相関していること

アメリカ教育省の成績に関わる統計調査(ECLS)によると、以下の項目が生徒の成績と相関している。

親の教育水準が高い
親の社会・経済的地位が高い
親がPTAの活動をやっている
家に本がたくさんある

つまり、インテリで金持ちで、子どもの教育に熱心ということだ。注意すべきは最後の項目で、子どもが本を読むかどうかは関係ない。本を読むことが大切だと思い、自身も本を読んでいる親のもとで育つことが成績にプラスの影響を与えたと考えられる。

03 7勝7敗力士が取り組む勝率は高い

この話のネタもとはつぎの書籍『ヤバい経済学』(スティーヴン・D・レヴィット/スティーヴン・J・ダブナー著)。統計の実践的な考え方と使い方を示す。

図001■スティーヴン・D・レヴィット/スティーヴン・J・ダブナー著『ヤバい経済学』

7勝7敗の力士は、そのつぎの取り組みで勝ち越しか負け越しかが決まる。共著者が調べた統計の結果はつぎのとおりだ。

vs	計算上	実統計

8勝6敗力士	48.7%	79.6%
9勝5敗力士	47.2%	73.4%

いずれも7〜8割と極めて高い勝率だ。考えられる要因としては以下が挙げられる。

結果の決まった相手は手を抜く

これは、他のスポーツの試合でもあり得る。それに加えて著者らは、以下の統計を導いた。

同じ相手との再戦では勝率40%
その後の勝率は普通に戻る

つまり、星の貸し借りをしていたことが見て取れる。統計から相撲の八百長疑惑があぶり出された。

04 宝くじは割りが最悪なギャンブル

その理由はつぎのとおり。

40%は自治体にピンハネされる
当選金には半分も充てられない
つまり期待値は50%にも満たない

加えて、たとえばジャンボ宝くじ1等の当選確率は1千万分の1だ。それは、つぎの確率に等しい。なお、落雷に遭う確率は、飛行機事故に遭う確率(1百万分の1)のさらに1/10らしい(『10億分の1の男』参照)。

したがって、つぎのことがいえよう。

統計と確率を学んだ者は、宝くじを買うべきではない

しかし、こう言い放った学者がいたらしい。

「宝くじは期待値でなく分散を買うのだ」

「分散」とは平均からのバラツキだ。分散が大きいと、外れるリスクは高くても、大儲けできる「可能性」がある。つまり、一攫千金を夢見るということだ。そこまで言い切るなら趣味の問題だろう。

趣味であれば、意味を説明しなくて構わない。たとえば、つぎのような例だ。

棒切れで地面のボールを打って
地面に掘られた穴に放り込む

何の意味があるのかわからない

あるいは、物理学的に無駄であってもよい。

雪の積もった山まで行って
わざわざ上に昇る
そして滑り降りる

位置エネルギーの無駄な消費

そう考えると、宝くじは社会的な意味があるといえる。本人も満足しているなら問題ない。

自治体に40%寄付して
半分に満たない当選金を争い
夢が見られたと満足する

社会貢献度は高い

[*1] つぎの記事は、子どもの頃に落雷に遭い、2015年に100万ドルの宝くじに当たった男性を紹介している(ごていねいに、彼の娘も落雷に遭って命をとりとめたという)。すごく運が悪いのか、よいのか判断に迷う。あたりすぎであることは間違いない。

世界のニュース「【カナダ】２度落雷に当たった男、宝くじにも当たる」

05 確率は直感を裏切ることがある

確率の高低は、しばしば直感や常識を裏切ることがある。たとえば、つぎの確率は思ったよりも高く感じられるのではないか。

サッカーの両チームと主審合わせて23人の中に、同じ誕生日の人がひと組以上見つかる確率は50%をわずかに上回る。

ここでは、その解説や計算には立ち入らない。興味のある方は、FumioNonaka.com Newsletter: no.011「同じ誕生日の人がいる確率」をお読みいただきたい。ちなみに、クラスが40人だと90%弱、50人なら約97%の確率で、同じ誕生日の人が見つかる。

06 モンティ・ホール問題

「モンティ・ホール問題」は、モンティ・ホールが司会者を務めるアメリカのゲームショー番組が由来となっている。この問題が公にされたとき、多数の数学者もこぞって反論したというほど、直感を裏切る結果が導かれる。

3つの扉のうちひとつの向こうに豪華賞品がある
挑戦者がそのひとつを選ぶ
するとモンティは選ばれなかった扉のうちハズレを開ける
そして1度だけ選択を変えてよいと告げられる

このとき、つぎの結果が導かれるというのだ。

選択を変えると当たる確率は倍になる

もとの選択が当たる確率は、1/3で間違いない。だが、選択を変えれば、その確率は2/3になるという(図002)。

図002■選択を変えると当たる確率は倍になる

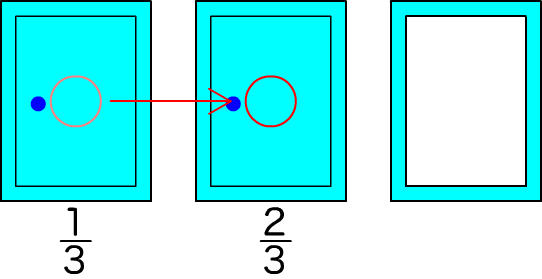
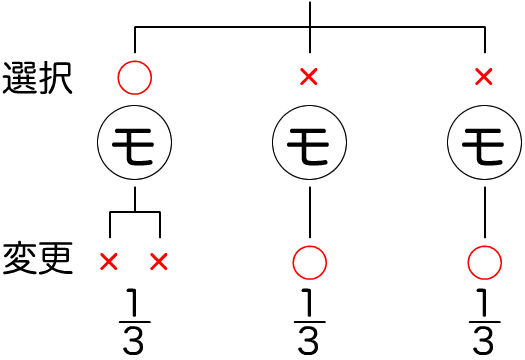
はじめは3つの扉のうちひとつに賞品があるのだから、当たる確率は1/3だ。しかし、つぎにモンティのターンになる(図003)。はじめの選択が当たりだったら、残る扉はいずれもハズレで、モンティはどちらを開いてもよい(図003左下)。ところが、はじめに外れを選んだとき、残るふたつのうちひとつは当たりで、モンティはもう一方の外れの扉を開くしか選択肢がない(図003下の真ん中と右)。つまり、選択を変えたとき、外れるのははじめに当たりを選んだ1/3の場合で、後のふたつの外れを選んでいたときはいずれも当たりになる。つまり、1/3の当たりが2本に増えたということだ。

図003■モンティの選択が確率を変える

3つの扉を52枚のカードにして考えよう。たとえば、スペードのAを当たりとしておく。52枚伏せて並べたカードから1枚を選ぶ(図004)。

図004■52枚伏せて並べたカードから1枚を選ぶ

3つの扉と同じ状況にするには、選んだ以外のカードから1枚だけ残して、その他の外れすべてを開くことになる。しかし、いちいち50枚のカードを開かなくても、残りのカードすべてをひと山に重ねても同じことになる(図005)。

図005■1枚だけ残してすべて開けるのは残りはひと山にするのと同じ

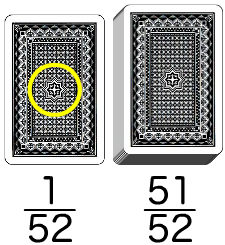
こうすると、選んだカードの当たる確率が1/52なのに対して、51枚のひと山を選んだら51/52であることが見てとれよう。このとき選択を変更するかしないか。ファイナルアンサー？

図006■選択を変更するかしないか

作成者: 野中文雄
作成日: 2016年6月25日