シンタックス
public function dotProduct(secondVector:Vector3D):Number
引数
secondVector:Vector3D ― 内積を計算するためのもうひとつのベクトルとなるVector3Dインスタンス。
戻り値
Vector3D ― 内積として計算された数値(スカラー)。ふたつのベクトル、つまり参照したVector3Dインスタンスとメソッドの引数に渡したもうひとつのVector3Dインスタンスとが互いに垂直な場合、内積として0が返ります。
説明
参照したVector3Dインスタンスと引数のVector3Dインスタンスとの内積を計算して、その結果となる数値(スカラー)を返します。内積はドット積(dot product)とも呼ばれます。ふたつのVector3DインスタンスmyVectorとsecondVectorの内積dotProductは、Vector3D.crossProduct()メソッドをつぎのように呼出して求めます。
|
var dotProduct:Number = myVector.dotProduct(secondVector)
|
数学ではベクトルmyVectorとsecondVectorの内積は、ふたつのベクトルのなす角をθとしたとき、以下の式で定義されます。なお、絶対値はベクトルの大きさを示します。
|myVector| |secondVector| cosθ
ふたつのベクトルが成す角度θは、静的メソッドVector3D.angleBetween()で調べられます。そして、ベクトルの大きさは、Vector3D.lengthプロパティの値です。したがって、ベクトルmyVectorとsecondVectorの内積を、以下の計算で求めることもできます。
|
var theta:Number = Vector3D.angleBetween(myVector,secondVector);
var dotProduct:Number = myVector.length * secondVector.length * Math.cos(theta);
|
内積の値により、ふたつのベクトルが直交するかどうかを調べることができます[*1]。ふたつのベクトルが直角を成すとき、内積は0になります。また、内積の値が正であれば鋭角、負の場合は鈍角を成します。
|
[*1] 後の「数学解説」で述べるとおり、内積と逆三角関数cos-1を使えば、ふたつのベクトルの成す角を求めることもできます。しかし、ActionScript 3.0には前述のVector3D.angleBetween()メソッドが備わっていますので、内積から角度を計算する必要はないでしょう。
|
数学解説[*2]
ふたつのベクトルをAとBとすると、その内積はつぎの式で定義されます。
A・B = |A||B|cosθ
他方、外積はA×Bで表されるベクトルです。外積の大きさ|A×B|は、AとBの成す角をθとすると、つぎの式で与えられます。
|A×B| = |A||B|sinθ
内積は大きさのみの値(スカラー)であるのに対して、外積がベクトルであることにご注意ください[*3]。
cosθは角度がπ/2(90度)のとき0となり、sinθは角度θが0のとき0になります。したがって、ベクトルAとBは互いに、内積の大きさが0のとき垂直、外積が0のときに平行となります。
3次元空間のベクトルAとBを、それぞれ(ax, ay, az)および(bx, by, bz)とすると、内積と外積はつぎの式で求められます[*4][*5]。
A・B = axbx + ayby + azbz
A×B = (aybz - azby, azbx - axbz, axby - aybx)
|
[*2] ベクトルやその外積および内積については、つぎのサイトが参考になります。平面幾何におけるベクトル演算「内積と外積」、基礎の基礎編その1「内積と外積の使い方」、「内積の意味」、「ベクトル其の参」。
[*3] ベクトルには、行列と異なり、べクトル同士の乗算は定義されていません。なお、演算を表す記号として外積が「×」内積は「・」を使うために、前者を「クロス積」(cross product)、後者を「ドット積」(dot product)と呼ぶことがあります。
[*4] この座標(成分)値から求めた内積を使って、ふたつのベクトルの成す角が求められます。前述の内積の定義より、以下のようにcosθが導けます。すると、逆三角関数cos-1により角度θが得られるからです。
A・B = |A||B|cosθ
cosθ = A・B/(|A||B|)
θ = cos-1(A・B/(|A||B|))
とくにふたつのベクトルの大きさがともに1の場合には、角度θは以下の式で求められます。なお、ベクトルの方向は変えず、大きさを1にすることは、ベクトルの「正規化」と呼ばれます。
θ = cos-1(A・B)
[*5] 内積A・Bを表すふたつの式、|A||B|cosθとaxbx + ayby + azbzの値が等しいことは自明ではありません。それを示すためには、余弦定理を用います。各辺の長さをそれぞれa、b、cとする以下の三角形において、余弦定理はつぎの等式で示されます(余弦定理の証明は省きます。興味がある方はネットで検索すれば、簡単に確かめられるでしょう)。
|
c2 = a2 + b2 - 2ab cosθ
cosθ = (a2 + b2 - c2)/2ab
|
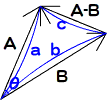 |
a、b、cは、それぞれベクトルA、B、A-Bの絶対値です。したがって、これらの項を入替えたうえで、上記cosθの式を内積の定義式に代入して、つぎのように変形することができます。
A・B = |A||B|cosθ
= |A||B|(|A|2 + |B|2 - |A-B|2)/2|A||B|
= (|A|2 + |B|2 - |A - B|2)/2
= ((ax2 + ay2 + az2) + (bx2 + by2 + bz2) - ((ax - bx)2 + (ay - by)2 + (az - bz)2))/2
= (2axbx + 2ayby + 2azbz)/2
= axbx + ayby + azbz
|
Player
ActionScript 3.0/Flash Player 10/AIR 1.5以降。
参考
[ActionScript 3.0言語およびコンポーネントリファレンス] > [Vector3D] > [dotProduct()メソッド]
[Flash CS4 Professional ActionScript 3.0 Language Reference] > [Vector3D] > [dotProduct() method]
作成者: 野中文雄
作成日: 2009年4月14日