1. 四元数とは
「四元数(しげんすう)」とは「クォータニオン(quaternion)」とも呼ばれ、ひとつの実数(スカラー)とひと組の3次元べクトルで表される数です[*1]。3次元べクトルは3つの要素で成立ちますので、ひとつのスカラーと計4つの数(元)で構成されるため、この名がついたのでしょう。
四元数は、4次元べクトルとしての性質をもちます。しかし、それに加えて、ベクトルにはない乗法が定義されています。とくに、四元数の乗算で、3次元座標空間における回転を表せることが特長です。
|
[*1] 実数をt、3次元べクトルをV = (x, y, z)としたとき、四元数Qは後述「3. 四元数の定義」のとおりつぎのように示されます。
Q = (t; V)
または
Q = (t; x, y, z)
|
2. 複素数
四元数は、複素数を拡張した数と捉えることができます。そこで、四元数を説明する前に、複素数について簡単におさらいしておきましょう。複素数は、実数にないiという虚数単位を用いて表します。iは2乗すると-1になります(i2 = -1)。任意のふたつの実数x、yに対して、複素数zはつぎの式で示されます。このときxとyを、それぞれ複素数zの実部ならびに虚部といいます。
z = x + yi
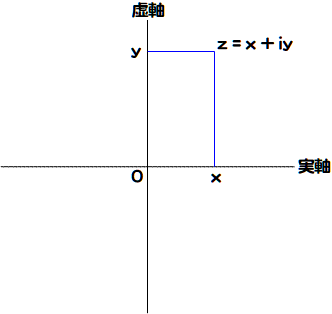
実数は、数直線上の任意の点で示すことができます。これに対して、複素数は、実部を横軸(実軸)、虚部を縦軸(虚軸)とする平面で表されます。この平面は「ガウス平面」と呼ばれます(図001)。また逆に、平面上の任意の点は、複素数に対応させることができます。
図001■ガウス平面で複素数を示す
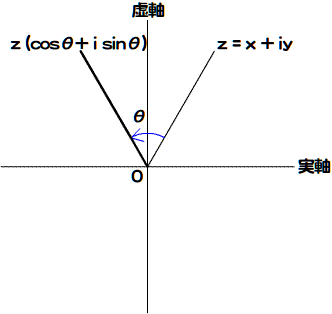
平面上の座標が表せるという点では、複素数は2次元のベクトルと似ています。しかし、ベクトルとは異なり、複素数は四則演算ができます。とくに、その乗算は座標の回転を表せます。任意の複素数zをガウス平面上で、原点から反時計回りにθ回転させるには、つぎの複素数を掛合わせます(図002)[*2][*3]。
cosθ + i sinθ
図002■cosθ + i sinθの乗算は座標をθ回転させる
|
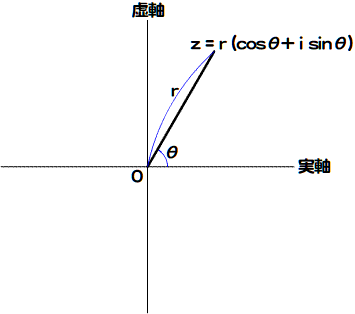
[*2] ガウス平面上において任意の複素数zの原点からの距離がrで、実軸となす角がθのとき、三角関数を使ってつぎのように表すことができます(図003。なお、三角関数と座標の関係については「角度と座標の計算 − Flash の三角関数を使う」をご参照ください)。
z = r(cosθ + i sinθ)
図003■ガウス平面上の複素数を距離rと角度θで表す
そこで、本文に述べたとおり複素数cosφ + i sinφを掛合わせると、この複素数zの座標を原点から反時計回りにさらにφ回転させることを示します。
z(cosφ + i sinφ)
= r(cosθ + i sinθ)(cosφ + i sinφ)
= r((cosθ cosφ - sinθ sinφ) + i(sinθ cosφ + cosθ sinφ))
ここで、加法定理より以下の等式が成立ちます。
cos(θ+φ) = cosθ cosφ - sinθ sinφ
sin(θ+φ) = sinθ cosφ + cosθ sinφ
これを前述の式に代入すると、つぎの関係が導かれます。
z(cosφ + i sinφ) = r(cos(θ+φ) + i sin(θ+φ))
これは、原点からの距離がrで実軸となす角がθの任意の複素数zに複素数cosθ + i sinθを乗じると、原点からの距離がr、実軸となす角がθ+φの座標に変換されたことを示します。つまり、原点からの距離はそのまま、角度がさらにφ回転されたということです。
[*3] 複素数について詳しくは、Wikipedia「複素数」、複素数の基礎「複素平面」、高校の数学「複素数」などをお読みください。
|
3. 四元数の定義[*4]
四元数には、虚数iと似たjとkという単位が加わります。これらはすべてiと同じく、2乗すると-1になります。
i2 = j2 = k2 = -1
四元数も複素数と同じように、四則演算ができます。ただし、乗法の交換法則は成立ちません。3つの単位の乗算結果は、つぎのように定義されています。
ij = k、ki = j、jk = i
ji = −k、ik = −j、kj = −i
これら3つの単位を用いて、任意の四元数Qは実数t、x、y、zに対してつぎのように表されます。このとき、tを実部、x、y、zの項を合わせて虚部といいます。
Q = t + ix + jy + kz
四元数Qは、虚部と実部を分けて、つぎのように表すことがあります。
Q = (t; x, y, z)
虚部は3つの値から成立つので、3次元ベクトルV = (x, y, z)と捉えられます。すると、四元数Qは、つぎのように示すこともできます。なお、実部をスカラー部、虚部はベクトル部と呼ぶこともあります。
Q = (t; V)
四元数Q = t + ix + jy + kzの絶対値|Q|は、以下のように定義されます。よって、|Q| = 0となるのは、t = x = y = z = 0のときだけです。
|Q| = √(t2 + x2 + y2 + z2)
また、共役四元数Q*というものが、つぎのように定義されています。
Q* = t - ix - jy - kz
四元数Qとその共役四元数Q*との積は、計算すると絶対値|Q|の2乗になります[*5]。
QQ* = Q*Q = t2 + x2 + y2 + z2
4. 四元数の計算
ふたつの四元数P = s + iu + jv + kwとQ = t + ix + jy + kzの計算についてご説明します。まず、加減算P±Qは単純で、実部と虚部を単位ごとにそれぞれ足し引きします。
P + Q = (s + iu + jv + kw)±(t + ix + jy + kz)
= (s±t) + i(u±x) + j(v±y) + k(w±z)
ベクトル表現にすると、もっと簡潔に表せます。
P + Q = (s; U)±(t; V)
= (s±t; U±V)
つぎに、乗算は項数が多いので、少し手間がかかります。ふたつの四元数の積PQは、以下のとおりです。すでに述べたように、四元数の乗法は交換法則が成立たないことにご注意ください。
PQ = (s + iu + jv + kw)(t + ix + jy + kz)
= (st − ux − vy − wz) + i(sx + ut + vz − wy) + j(sy − uz + vt + wx) + k(sz + uy − vx + wt)
ベクトル表現にすると、ベクトルの演算を用いて、乗算も簡潔に表すことができます。なお、ベクトルUとVとの計算で、U・Vは内積、U×Vは外積を意味します[*6]。
PQ = (s; U)(t; V)
= (st - U・V; sV + tU + U×V)
4. 四元数による3次元座標空間の回転
四元数を用いると3次元座標空間の回転が簡潔に表せ、行列を使うより計算も楽になります。
まず、3次元座標空間における任意の点は、3次元位置ベクトルP = (x, y, z)で示されます。この3次元ベクトルは、以下のようにスカラー部を0とした四元数で表すことができます。
X = (0; P)
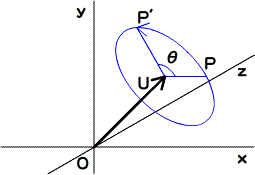
つぎに、回転の軸となる任意の単位ベクトルU = (u, v, w)を定めます。単位ベクトルですので|U| = 1です。このとき、位置ベクトルPを回転軸Uで角度θ回した座標P'は(図004)、つぎのような四元数Qとその共役四元数Q*を使って、四元数X' = (0; P')のベクトル部P'として求めることができます。
Q = (cos(θ/2); sin(θ/2)U)
X' = QXQ*
図004■任意の単位ベクトルUを軸として位置ベクトルPをθ回転させる
このX'をさらに別の単位ベクトルU'でφ回転させたいときは、同じように四元数Rを使って共役四元数R*と挟み込んで乗算します。
R = (cos(φ/2); sin(φ/2)U')
X'' = RX'R* = RQXQ*R*
このように四元数による3次元座標空間の回転では、直交座標のxyz軸にかぎらず[*7]、任意のベクトルを軸に指定できます。また、3次元座標空間の回転などを扱う変換行列が4×4の計16要素で構成されるのに対して、四元数は4つの値だけで回転を表すことができます。そのため、演算の処理効率は高くなります。ただ、四元数を構成する値の意味が、直感的にわかりにくいという難点もあります。
|
[*7] xyzの各軸による角度θの回転を表す四元数は、つぎのとおりです。
x軸: (cos(θ/2); sin(θ/2), 0, 0)
y軸: (cos(θ/2); 0, sin(θ/2), 0)
z軸: (cos(θ/2); 0, 0, sin(θ/2))
|
5. ActionScript 3.0で使われる四元数
ActionScript 3.0には、四元数をつくりその演算を行うというクラスはありません。ただ、Matrix3Dクラスに回転の四元数表現を扱うメソッドとして、Matrix3D.decompose()とMatrix3D.recompose()が備わっています[*8]。
前者は、変換行列のMatrix3Dインスタンスから、平行移動、回転、拡大/縮小の各設定値をVector3Dをベース型とするVectorインスタンスとして取出すメソッドです。後者のメソッドは、逆に平行移動、回転、拡大/縮小の各設定値のVector3DをVectorインスタンスに格納して、Matrix3Dインスタンスに設定します。
これらのメソッドを使うとき、方向スタイルの引数として定数Orientation3D.QUATERNIONを指定すると、回転の設定であるVector3Dインスタンスの値が四元数として計算されます[*9][*10]。
|
[*8] Matrix3D.interpolate()およびMatrix3D.interpolateTo()メソッドも、四元数について触れています。しかし、これらのメソッドでは、四元数が内部的な処理として使われていることを説明しているだけです。
[*9] このときVector3D.wプロパティの値が、四元数の実(スカラー)部を示します。同プロパティの[ヘルプ]の説明に、この値が「回転角度」を表すように書かれているのは正確ではありません。
[*10] たとえば、y軸回りの60度(π/3ラジアン)の回転を表す四元数Qは、前述注[*7]のとおりつぎのようになります。
Q = (cos(π/3/2); 0, sin(π/3/2), 0) = (cos(π/6); 0, sin(π/6), 0)
変換行列Matrix3Dインスタンスに60度回転(Matrix3D.appendRotation()メソッド)の変換を加えたうえで、Matrix3D.decompose()メソッドで回転の設定となるVector3Dインスタンスを取出し、その値を確かめてみましょう(スクリプト001)。
スクリプト001■60度回転した変換行列から回転の設定となる四元数の値を調べる
|
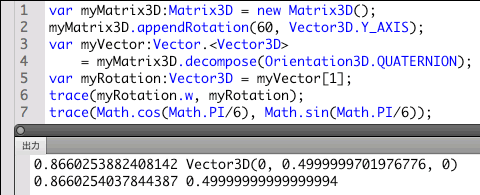
// フレームアクション
var myMatrix3D:Matrix3D = new Matrix3D(); // 変換行列生成
myMatrix3D.appendRotation(60, Vector3D.Y_AXIS); // 60度回転
// 平行移動、回転、拡大/縮小の設定値を納めたVectorインスタンスの取得
var myVector:Vector.<Vector3D> = myMatrix3D.decompose(Orientation3D.QUATERNION);
var myRotation:Vector3D = myVector[1]; // 回転の四元数表現となるVector3D取得
trace(myRotation.w, myRotation);
trace(Math.cos(Math.PI/6), Math.sin(Math.PI/6));
|
[出力]結果を見ると、回転の四元数表現となるVector3DのVector3D.wプロパティの値はcos(π/6)、3次元ベクトルの値が(0, sin(π/6), 0)に等しくなっています(図005)。ただし、Math.cos()およびMath.sin()メソッドの値と比べると、若干の誤差が生じているようです。
図005■回転の四元数表現となるVector3Dの値を[出力]
|
作成者: 野中文雄
更新日: 2010年4月1日 注[*2]の計算の過程にあった誤りを訂正。
作成日: 2009年5月4日