サイトトップ
Director Flash 書籍 業務内容 プロフィール

Adobe Flash非公式テクニカルノート

インスタンスをドラッグで回して動かす

ID: FN1009003 Product: Flash CS3 and above Platform: All Version: 9 and above/ActionScript 3.0

インスタンスをドラッグして回したり、マウスボタンを放して滑らせるアニメーションについて解説します。以下のwonderflのサンプルはクラスとして定義していますが、本稿は要点がわかりやすいようにフレームアクションを基本に説明します。

Dragging and rotating a card with the Matrix class - wonderfl build flash online


01 ふたつの課題
このお題では、課題がふたつあります。第1に、マウスクリックした点が中心になるようにインスタンスを回すことです。やり方としては、三角関数で座標を調整するか、変換行列(Matrixクラス)を使うことが考えられます。本稿は、3次元座標空間の扱い(Matrix3Dクラス)にも応用の利く後者の方法を採ります。

第2の課題は、マウスポインタの動きをどのように回転の速さに反映させるかです。物理学に「力のモーメント」の公式があり、計算には「ベクトルの外積」を用います。むずかしそうな響きがするものの、計算そのものは四則演算で済みます。

動作の組立てはつぎのとおりです。インスタンスの上でマウスボタンをクリックするとドラッグが始まり、インスタンスはその動きに応じて回ります。マウスボタンを放せば、インスタンスはその勢いで減速しながら滑っていきます。すると、イベントリスナーは、マウスボタンをインスタンス上で押したとき(InteractiveObject.mouseDownイベント/定数MouseEvent.MOUSE_DOWN)と放したとき(InteractiveObject.mouseUpイベント/定数MouseEvent.MOUSE_UP)に、つぎのように処理することになります。なお、フレームアクションは、ドラッグするMovieClipシンボルに書くものとします(図001)。

    // フレームアクション
    // ドラッグするMovieClipインスタンスに記述
  1. addEventListener(MouseEvent.MOUSE_DOWN, xMouseDown);
  2. function xMouseDown(eventObject:MouseEvent):void {
  3.   removeEventListener(Event.ENTER_FRAME, xThrow);   // [*1]
  4.   addEventListener(Event.ENTER_FRAME, xDrag);
  5.   stage.addEventListener(MouseEvent.MOUSE_UP, xMouseUp);
  1. }
  2. function xMouseUp(eventObject:MouseEvent):void {
  3.   removeEventListener(Event.ENTER_FRAME, xDrag);
  4.   stage.removeEventListener(MouseEvent.MOUSE_UP, xMouseUp);
  5.   addEventListener(Event.ENTER_FRAME, xThrow);
  6. }
  7. function xDrag(eventObject:Event):void {
      // ドラッグした点でインスタンスを回す
  1. }
  2. function xThrow(eventObject:Event):void {
      // 減速しながら滑る
  1. }
図001■ドラッグして回すMovieClipシンボルにフレームアクションを記述する
図001左図 図001右図

ふたつの課題は、ドラッグした点でインスタンスを回すDisplayObject.enterFrameイベントのリスナー関数xDrag()で問われます。そこで本稿は、この関数xDrag()の処理を中心に解説し、フレームアクション全体は最後にスクリプト001として掲げます。上に抜粋したフレームアクションの行番号は、このスクリプト001にもとづきます。

[*1] インスタンスを初めてクリックしたとき(InteractiveObject.mouseDownイベント)、DisplayObject.enterFrameイベント(定数Event.ENTER_FRAME)にはリスナー関数が登録されていません。その場合にEventDispatcher.removeEventListener()メソッドを呼出しても、効果がないだけで、とくにエラーなどの問題は起こりません。

02 インスタンスを任意の点で回す
Matrixクラスを使うと、インスタンスの伸縮や回転ができます。インスタンスに適用されているMatrixオブジェクトは、DisplayObject.transformプロパティの参照からTransform.matrixプロパティとして得られます。Matrixは数学の「行列」を意味し、座標の変換を行います。座標変換のためのパラメータ(成分)をもった行列は、「変換行列」と呼ばれます[*2]。

変換行列による座標変換で注意しなければならないのは、変換の原点が動かせないことです。Matrixクラスで伸縮や回転を加えると、つねに親インスタンスの基準点が原点になります。[自由変形ツール]でいうなら、中心点が親タイムラインの基準点に固定されるようなものです(図002)。

図002■[自由変形ツール]で親タイムラインの基準点を中心点にする
図002左図 図002右図

Flashを使い始めたとき、おそらく動かせなくて誰もがつまずくのはシンボルの基準点でしょう。解決方法は、コロンブスの卵でした。基準点が動かないのなら、中身を動かせばよいのです。実は、Matrixクラスにはもうひとつ、座標を動かす平行移動という変換があります。この平行移動を加えれば、任意の点を中心にインスタンスを伸縮あるいは回転できます。

まず、変換の中心にしたい点を親インスタンスの基準点に平行移動します。つぎに、伸縮や拡大をすれば、中心にしたい点が親インスタンスの基準点となって変換されます。そのうえで、インスタンスを改めてもとの位置に戻せばよいのです(図003)。

図003■親インスタンスの基準点に移動して変形したうえでもとの位置に戻す
図003左図
(1)親インスタンスの基準点に移動 		図003中図
(2)伸縮・回転 		図003右図
(3)もとの位置に戻す

Matrixクラスの平行移動や伸縮あるいは回転のメソッドは、つぎに掲げるとおりです。DisplayObject.transformプロパティから得たTransform.matrixプロパティの参照に対してこのメソッドを呼出したうえで、そのMatrixオブジェクトを改めてインスタンスのDisplayObject.transformプロパティに設定する必要があります。

【平行移動】
Matrixオブジェクト.translate(水平移動ピクセル, 垂直移動ピクセル)
【伸縮】
Matrixオブジェクト.scale(水平伸縮率, 垂直伸縮率)
【回転】
Matrixオブジェクト.rotate(回転ラジアン角)

たとえば、タイムラインに置いたインスタンスmy_mcを自身の基準点で30度回し、縦横120%に拡大するには、つぎのようなフレームアクションを書きます(図003参照)。Matrixオブジェクトにメソッドで変換を適用するだけでは足りず、そのオブジェクトを改めてDisplayObject.transformプロパティのTransform.matrixプロパティに設定していることにご注意ください。

var myMatrix:Matrix = my_mc.transform.matrix;   // Matrixオブジェクトを取得
var nX:Number = my_mc.x;
var nY:Number = my_mc.y;
myMatrix.translate(-nX, -nY);   // 親インスタンスの基準点に移動
myMatrix.rotate(30 * Math.PI / 180);   // 30度回転
myMatrix.scale(1.2, 1.2);   // 120%に拡大
myMatrix.translate(nX, nY);   // もとの位置に戻す
my_mc.transform.matrix = myMatrix;   // Matrixオブジェクトを設定

後掲スクリプト001では、DisplayObject.enterFrameイベントのリスナー関数xDrag()は、基本的に同じ考え方によりドラッグした点でインスタンスを回します。

この関数はふたつのアニメーションを行います。ひとつは、マウスポインタの新たな位置にインスタンスを移動します。もうひとつは、直前のマウスポインタの位置からの動きに応じてインスタンスを回します。そのために、新たなマウスポインタの座標をスクリプト第21行目で調べるとともに、直前の座標は第31行目で変数(lastMouse)に保持します[*3]。

実際には、先に回転をします。よってスクリプト第27行目で、直前のマウスポインタの位置が親タイムラインの基準点と重なるように、インスタンスを移動します。そして、第28行目でその点を中心に回します。回す角度の計算は、次項で解説します。そのうえで第29行目は、インスタンスを新たなマウスポインタの位置に移動しています。

  1. var myMatrix:Matrix;
  2. var lastMouse:Point;
  1. function xDrag(eventObject:Event):void {
  1.   var currentMouse:Point = new Point(parent.mouseX, parent.mouseY);
  1.   myMatrix = transform.matrix;
  2.   myMatrix.translate(-lastMouse.x, -lastMouse.y);
  3.   myMatrix.rotate(angularVelocity);
  4.   myMatrix.translate(currentMouse.x, currentMouse.y);
  5.   transform.matrix = myMatrix;
  6.   lastMouse = currentMouse.clone();
  1. }

なお、初めてインスタンスをクリックしてリスナー関数xDrag()が呼ばれたときは、このままでは直前のマウスポインタの座標が変数(lastMouse)にありません。そこで、InteractiveObject.mouseDownイベントのリスナー関数xMouseDown()にスクリプト第12行目を加えて、変数に初期値を設定します。

  1. addEventListener(MouseEvent.MOUSE_DOWN, xMouseDown);
  2. function xMouseDown(eventObject:MouseEvent):void {
  3.   removeEventListener(Event.ENTER_FRAME, xThrow);
  4.   addEventListener(Event.ENTER_FRAME, xDrag);
  5.   stage.addEventListener(MouseEvent.MOUSE_UP, xMouseUp);
  6.   lastMouse = new Point(parent.mouseX, parent.mouseY);   // 追加
  7. }

[*2] 変換行列の数学的な説明については「変換行列を数学的に捉える」をお読みください。また、Matrixクラスについては、Adobeデベロッパーセンター「Matrixクラス − 変換行列」を併せてご参照ください。

[*3] 変数(lastMouse)に単純にPointオブジェクト(変数currentMouseの値)を代入すると、ふたつの変数が同じオブジェクトを参照してしまいます。そのため、Point.clone()メソッドでオブジェクトを複製したうえで代入しました。

もっとも、currentMouseはローカル変数で、しかもスクリプト第21行目は毎回新たなPointオブジェクトを設定しています。したがって、この処理にかぎれば、そのまま代入しても問題はありません。とはいえ、それぞれの変数に異なった操作をするつもりのときは、複製をしておく方が安心でしょう。

03 回す動きを反映させる
マウスポインタの動きに応じてインスタンスを回転しようとした場合、それをどのように反映すればよいのか考えなければなりません。かたちの変わらない固いもの(「剛体」といいます)に回す力を加えるとき、物理学では「力のモーメント」というベクトルでその働きを表します[*4]。

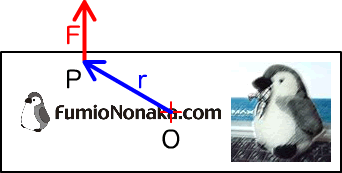
下図004のように重心がOにあるものの点Pに力を加えたとします。このときOPをベクトルr、点Pに加えた力をベクトルFで示すと、力のモーメントはふたつのベクトルの外積r×Fで表されます(記号「×」は乗算ではなく外積を意味します)。3次元空間における場合、ふたつのベクトルの成分(座標値)がr(rx, ry, rz)とF(Fx, Fy, Fz)で与えられれば、外積r×Fのベクトルの成分(座標値)はつぎの式で導かれます[*5]。

r×F = (ryFz - rzFy, rzFx - rxFz, rxFy - ryFx)

今回の2次元平面の場合には、外積はスカラー(実数値)になって扱いはもっと簡単です。ふたつのベクトルの成分(座標値)がr(rx, ry)とF(Fx, Fy)で与えられたとき、外積r×Fはつぎの式のとおりです。この値が大きいほど、回す力が大きく働くことを示します。また、値の正負が回転の方向を決め、正が時計回りです。

r×F = rxFy - ryFx

図004■力のモーメントを求める
図004

この2次元ベクトルの外積の計算は、後掲スクリプト001に関数crossProduct2D()として定義しました。引数の2次元ベクトルは、Pointオブジェクトで扱っています。

  1. function crossProduct2D(point0:Point, point1:Point):Number {
  2.   return point0.x * point1.y - point0.y * point1.x;
  3. }

さて、この力のモーメントの計算をリスナー関数xDrag()に組込んでいきます。まず、座標とベクトルはPoint型の変数で扱います(図005)。ドラッグするインスタンスの基準点を中央に設定したうえで、その座標はローカル変数positionに納めます。前項ですでにご紹介したとおり、マウスポインタの直前の座標と新しい座標は、それぞれ変数lastMouseとローカル変数currentMouseにもたせます。

すると、力のモーメントを求めるためのふたつのベクトルr(ローカル変数radius)とF(ローカル変数force)が、位置座標(ベクトル)の引き算でつぎのように導かれます。ベクトルの計算は、終点から始点の座標を差引きます。

radius = lastMouse - position
force = currentMouse - lastMouse

図005■座標とベクトルをPoint型の変数で扱う
図005

力のモーメントの計算を組込んだリスナー関数xDrag()は、以下のとおりです。まずスクリプト第20〜21行目で、インスタンスの座標(重心)と新たなマウスポインタの座標をPointインスタンスとして生成します。つぎに第22行目〜23行目は、それらの座標(ベクトル)の引き算により、力のモーメントの計算に必要なふたつのベクトルを求めます。引き算のメソッドはPoint.subtract()です。そして第24行目が、上にご紹介した関数crossProduct2D()により、ふたつのベクトルの外積を計算します。

もっとも、求められた外積(moment)は座標値の掛け算と引き算ですので、大きな数値になることもあります。他方で、パラメータとして渡すMatrix.rotate()メソッドの引数はラジアン値の角度です。桁の差が大きいので、スクリプト第2行目に調整の定数を設定しました[*6]。第25行目は、外積の値にその定数を乗じたうえで、角度の変数(angularVelocity)に加速度として足し込みます。もちろん、減速も必要です。そこで、第1行目に減速率を定めて、第33行目で角度の値に乗じました。

  1. const DECELERATION:Number = 0.8;
  2. const RATIO:Number = 0.01 * Math.PI / 180;
  3. var myMatrix:Matrix;
  4. var lastMouse:Point;
  1. var angularVelocity:Number = 0;
  1. function xDrag(eventObject:Event):void {
  2.   var position:Point = new Point(x, y);
  3.   var currentMouse:Point = new Point(parent.mouseX, parent.mouseY);
  4.   var radius:Point = lastMouse.subtract(position);
  5.   var force:Point = currentMouse.subtract(lastMouse);
  6.   var moment:Number = crossProduct2D(radius, force);
  7.   angularVelocity += moment * RATIO;
  8.   myMatrix = transform.matrix;
  9.   myMatrix.translate(-lastMouse.x, -lastMouse.y);
  10.   myMatrix.rotate(angularVelocity);
  11.   myMatrix.translate(currentMouse.x, currentMouse.y);
  12.   transform.matrix = myMatrix;
  13.   lastMouse = currentMouse.clone();
  1.   angularVelocity *= DECELERATION;
  2. }

これで、ドラッグした点でインスタンスを回すアニメーションの処理はできあがりました。

[*4] 実際に固いものを回そうとすれば、慣性なども働きます。けれど、現実のシミュレーションを目指す訳ではありませんので、それらは考えないものとします。

[*5] 力のモーメントの計算については、「力のモーメント」をご参照ください。

[*6] 定数の値(右辺)にラジアンと度数の換算比率(Math.PI / 180)を乗じたことには、深い意味はありません。数値がかなり小さくなるので、調整しやすいようにつけ加えた比率です。

04 マウスボタンを放したら滑らせる
残るは、インスタンスを減速しながら滑らせるリスナー関数xThrow()だけです。もっとも、慣性で移動しつつ回るだけですから、いわば関数xDrag()の処理を簡単にした内容です。そこで、スクリプト001の全体をお見せしましょう。

関数xThrow()のスクリプト第36〜40行目は、もうおなじみのインスタンスを回して移動する処理です。手順も関数xDrag()と同じ(第26〜30行目)で、引数が少し違うだけです。インスタンスの座標(重心)を親インスタンスの基準点に移し(第36行目)[*7]、減速率を乗じた角度で回転します(第37行目)。そして、もとの座標に慣性による移動(velocity)を加えた位置に戻しました(第38行目)。

この移動ベクトル(velocity)は、関数xDrag()で最後に操作したマウスの移動ベクトル(force)をスクリプト第32行目で代入したものです。この変数(velocity)値は、関数xDrag()の処理ではまったく使わず、関数xThrow()に引継ぐために宣言されました(第5行目)。

あとは、スクリプト第41〜42行目で移動と回転の減速をします。Point.normalize()メソッドは、ベクトルの大きさを引数の値にします。現在のベクトルの大きさは、Point.lengthプロパティで調べます。インスタンスの動きが小さくなったら、第43〜45行目がこのイベントリスナーを削除します。

スクリプト001■インスタンスをドラッグで回して動かす
    // フレームアクション
    // ドラッグするMovieClipインスタンスに記述
  1. const DECELERATION:Number = 0.8;
  2. const RATIO:Number = 0.01 * Math.PI / 180;
  3. var myMatrix:Matrix;
  4. var lastMouse:Point;
  5. var velocity:Point;
  6. var angularVelocity:Number = 0;
  7. addEventListener(MouseEvent.MOUSE_DOWN, xMouseDown);
  8. function xMouseDown(eventObject:MouseEvent):void {
  9.   removeEventListener(Event.ENTER_FRAME, xThrow);
  10.   addEventListener(Event.ENTER_FRAME, xDrag);
  11.   stage.addEventListener(MouseEvent.MOUSE_UP, xMouseUp);
  12.   lastMouse = new Point(parent.mouseX, parent.mouseY);
  13. }
  14. function xMouseUp(eventObject:MouseEvent):void {
  15.   removeEventListener(Event.ENTER_FRAME, xDrag);
  16.   stage.removeEventListener(MouseEvent.MOUSE_UP, xMouseUp);
  17.   addEventListener(Event.ENTER_FRAME, xThrow);
  18. }
  19. function xDrag(eventObject:Event):void {
  20.   var position:Point = new Point(x, y);
  21.   var currentMouse:Point = new Point(parent.mouseX, parent.mouseY);
  22.   var radius:Point = lastMouse.subtract(position);
  23.   var force:Point = currentMouse.subtract(lastMouse);
  24.   var moment:Number = crossProduct2D(radius, force);
  25.   angularVelocity += moment * RATIO;
  26.   myMatrix = transform.matrix;
  27.   myMatrix.translate(-lastMouse.x, -lastMouse.y);
  28.   myMatrix.rotate(angularVelocity);
  29.   myMatrix.translate(currentMouse.x, currentMouse.y);
  30.   transform.matrix = myMatrix;
  31.   lastMouse = currentMouse.clone();
  32.   velocity = force;
  33.   angularVelocity *= DECELERATION;
  34. }
  35. function xThrow(eventObject:Event):void {
  36.   myMatrix = transform.matrix;
  37.   myMatrix.translate(-x, -y);
  38.   myMatrix.rotate(angularVelocity);
  39.   myMatrix.translate(x + velocity.x, y + velocity.y);
  40.   transform.matrix = myMatrix;
  41.   velocity.normalize(velocity.length * DECELERATION);
  42.   angularVelocity *= DECELERATION;
  43.   if (Math.abs(angularVelocity) < 0.1 && velocity.length < 0.1) {
  44.     removeEventListener(Event.ENTER_FRAME, xThrow);
  45.   }
  46. }
  47. function crossProduct2D(point0:Point, point1:Point):Number {
  48.   return point0.x * point1.y - point0.y * point1.x;
  49. }

[*7] 拘束のない自由な剛体は重心回りに運動しますので、基準点で回転してもとくに不自然さはないでしょう(物理のかぎしっぽ「剛体ってなんだろう？」)。

作成者: 野中文雄
作成日: 2010年9月30日
Copyright © 2001-2012 Fumio Nonaka.  All rights reserved.