• 03-01 cos(コサイン)とsin(サイン)
• 03-02 円と楕円の方程式
• 03-03 ラジアン
• 03-04 tan(タンジェント)とtan^-1(アークタンジェント)
• 03-05 座標軸の方向について

○03-01 cos(コサイン)とsin(サイン)
三角関数は、角度を座標に変換するための関数です。したがって、角度と座標を扱った計算で使われます。

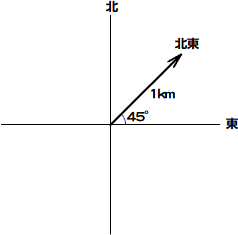
2次元の座標は、通常x軸とy軸が垂直に交わった直交座標系(空間)上のxy座標値で示されます。しかし、位置の表し方は、ほかにもあります。たとえばレーダーは、「北東1kmの地点」というように、方向と距離で目的地を指定します(図Math03-001)。方向とはつまり角度で、北東はx軸方向である東に対して、反時計回りに45度を意味します。

では、距離と方向で示された位置を、xy座標に直すにはどうしたらよいでしょう。そのために定義されたのが、三角関数のcos(コサイン)とsin(サイン)です。距離が1の場合を基本として考え、x軸に対して角度がθのときのxy座標は(cosθ, sinθ)で表します。これが、cosとsinの定義です。

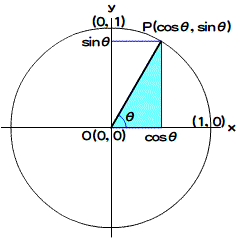
もう少し正確に述べましょう。x軸とy軸の直交座標で、原点O(0, 0)を中心とした半径1の円を「単位円」と呼びます。すると、単位円周上の任意の点Pが、点Pと原点Oを結んだ直線OPとx軸との角度θにより、x座標はcosθ、y座標がsinθと定義されることになります(図Math03-002)。

したがって、距離がrであれば、xy座標それぞれにrを掛けて、座標(r・cosθ, r・sinθ)で表されます(記号「・」は、「×」と同じく乗算を意味します)。

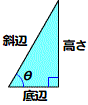
ここまでの説明を見て、高校のときに習ったsinやcosの定義と違うと思われる読者もいるかもしれません。高校では初めはおそらく、直角三角形の斜辺と他の2辺との比、つまり三角比で覚えたでしょう(図Math03-003)。

sinθ = 高さ/斜辺 cosθ = 底辺/斜辺

もちろん、三角比の定義も、正しいものです。しかし、比率という計算に目が奪われてしまうと、その意味を見失いがちです。

たとえば、円周率πは、円周の半径に対する比率(π=円周/半径)です。しかし、実際にその比率を、割り算で計算してみた人は少ないでしょう。ましてや、その比率の計算を今後行う可能性は、普通の人なら皆無です。

円周率πは、(それだけではありませんが)円の半径から面積を求めるための比率です。比率そのものは近似値3.14を使うか、コンピュータの計算に任せてしまえます。

同じように、cosやsinは、距離(r)と角度(θ)で示された位置を、xy座標(r・cosθ, r・sinθ)に変換するための関数なのです。そして、sinθやcosθの値(比率)が実際いくつになるかは、コンピュータに委ねるべき計算です。

○03-02 円と楕円の方程式
前節03-01の説明から、円と楕円の方程式をそれぞれ導くことができます。

●円の方程式
原点O(0, 0)を中心とした半径rの円周上の任意の点P(x, y)は、直線OPとx軸が成す角をθとすれば、(r・cosθ, r・sinθ)になります。したがって、原点Oを中心とした半径rの円の方程式は、角度θを用いてつぎのように表すことができます(図Math03-004)。

x = r・cosθ y = r・sinθ

●楕円の方程式
円に対して垂直方向もしくは水平方向に、拡大・縮小の変形をすれば楕円になります。この変形は具体的には、円周のxy座標のいずれか、または両方に対して、拡大・縮小比率としての係数を掛合わせます。

原点O(0, 0)を中心として、x軸と±a、y軸とは±bで交わる楕円の方程式は、以下のとおりです(図Math03-005)。これは原点Oが中心で半径aの円の方程式をもとに、y座標にb/aを掛合わせたことになります。

x = a・cosθ y = b・sinθ

原点0(0, 0)を中心とした半径aの円は、つぎの方程式で表されます。

x = a・cosθ
y = a・sinθ

y座標を示す下の方程式の右辺に変形の比率としてb/aを掛ければ、上図Math03-005の楕円の方程式が導かれます。

○03-03 ラジアン
三角関数を使った計算をする場合、角度の単位として度数ではなくラジアンを使うことが少なくありません。実際、ActionScriptで三角関数をメソッドとして備えるMathクラスでは、角度を指定する引数の値はラジアンが単位とされています。

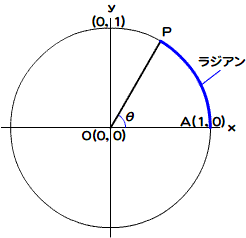
ラジアンは、角度を単位円の弧の長さで示す単位です。単位円の中心O(0, 0)と円周上の点Pとを結んだ直線OPがx軸と成す角をθとすると、単位円とx軸との正方向の交点A(1, 0)から点Pまでの円弧APの長さが、ラジアンを単位としたθの角度になります(図Math03-006)。

360°= 2πラジアン

単位円の半径は1ですから、円周の長さは2π(= 1×2×π)となり、360度は2πラジアンになります。1ラジアンは約57.29578度(= 360/2π)です。さて、ラジアンの測り方はわかったとしても、なぜこのような半端な値を使うのでしょう。

それは、数学の解析や物理で運動を扱う際に、ラジアンを単位とした方が便利だからです。たとえば、半径1mの円周上を、等速で回転している物体があったとします。測ってみたところ、1秒間に1ラジアン回転しました。そのときの物体の速さは、秒速1mになります。

半径1mの円周上の角度1ラジアン分の弧の長さは、半径と等しくなるからです。これがもし度数で約60度と示されたら、60度の弧の長さを計算しなければなりません。ラジアンを使えば、角度と長さとの換算が、単に半径を掛合わせるだけで済むのです。

とはいえ、ActioinScriptでインスタンスの回転角を定めるプロパティDisplayObject.rotationは、度数を単位とします。インスタンスのアニメーションで三角関数を使う際には、度数とラジアンとの換算が必要になる場合も少なくありません。そこで、度数とラジアンとの間の変換比率を示しておきましょう。360度が2πラジアンであることから、比率は簡単に求められます。

度数/360 = ラジアン/2πより、度数/180 = ラジアン/π。したがって、つぎの式が導かれます。

度数 = (ラジアン/π)×180 = ラジアン・(180/π)

ラジアン = (度数/180)×π = 度数・(π/180)

○03-04 tan(タンジェント)とtan^-1(アークタンジェント)

tanθ = y/x

直線OPを延ばして直線x = 1と交わった点をQとすると、その座標は(1, tanθ)で表されます(図Math03-007)。なお、0による割り算は定義されていませんので、xが0の場合のtanθは存在しません。また、xが0のとき点Pはy軸上にあるため、直線OPは直線x = 1と平行となり、交点Qが存在しないと考えてもよいでしょう。

[*筆者用参考]「三角関数の定義」

三角関数は、角度から座標を求める関数です。しかし、逆に座標から角度を求めたい場合もあります。一般に関数y = f(x)について、逆にyからxを求める関数が考えられるとき、その関数をf(x)の「逆関数」と呼び、x = f^-1(y)と表します(もう少し正確には、後述Maniac! Math03-007「関数と逆関数」参照)。

三角関数にも逆三角関数が定義されています。cos、sin、tanのそれぞれに対応して、cos^-1(アークコサイン)、sin^-1(アークサイン)、tan^-1(アークタンジェント)と表されます。

とくにtanは、xy座標(x, y)からtanθ = y/xが簡単に求まります(cosやsinでは、三角比の斜辺である座標までの距離r = √x²+y²を計算しなければなりません)。ですから、その逆関数tan^-1(y/x)を使えば、角度θもすぐに求められそうです。

[*筆者用参考]「三角法と弧度法」、Wikipedia「三角関数」。

ところが、逆三角関数には、重大な注意があります。ここでは、tanとtan^-1を例にしてご説明します。たとえば、tan(π/3)(=tan(60°))は√3です。そして、角度にπ(=180°)を加えたtan(4π/3)(=tan(240°))も同じく√3になります。

単位円上の点P(x, y)と原点を結んだ直線OPがx軸と成す角をθとすると、tanθ = y/xでした。角度θにπを加えた場合の単位円上の点をRとすると、その座標は(-x, -y)になります。したがって、tan(θ+π) = -y/(-x) = y/xとなり、tanθに等しいのです(図Math03-008)。

関数は、値がただひとつに定まらなければなりません。その点で、tanは問題ありません。tanθとtan(θ+π)の値がたまたま同じだとしても、角度からtanの値はただひとつに決まります。ところが、逆関数tan^-1は違います。tanが√3の値を取る角度は、π/3(= 60°)のほか4π/3(= 240°)など、無数に存在してしまいます。

そこで、tan^-1の値は-π/2(=-90°)より大きくπ/2(=90°)未満の値にかぎることとされました。いわば、単位円の座標のうち、x>0となる右半分のみで考えるということです。そうすれば、与えられたtanの値(y/x)に対して、tan^-1の値(θ)がただひとつに決まります。

実際には、単位円の半分の範囲(π = 180°)では足りず、円周上(2π = 360°)のすべての座標に対して角度を求めたいことが普通です。そのためには、tan-1を用いる際にx<となる単位円の左半分は場合分けをして、別途(角度からπ=180°を差引いて)計算することになります。

Math.atan()メソッドを使って、ActionScriptで処理を記述しても、さほど難しいスクリプトではありません。しかし、需要の多い処理なので、Mathクラスには2π(= 360°)の範囲の角度を返す特別なメソッドMath.atan2()がすでに定義されています。

Math.atan()メソッドとは異なり、Math.atan2()にはy/xの値を渡すのではなく、yとxとを別個にふたつの引数として指定します。そうすることで、xの値の正負を内部的に判別して、-πからπまでの2πの範囲の値を返すことが可能になったのです(表Math03-002)。

Math.atan2()メソッドに、y座標、x座標の順にふたつの引数を渡すと、原点(0, 0)と座標を結んだ直線の水平線と成す角度がラジアン値で返されます。なお、atan2もしくはそれに相当する関数は、数学上は存在しません。

たとえば、Math.atan2(√3, 1)は、底辺が1高さ√3の直角三角形の底辺と斜辺との間の角度ですから、π/3(= 60°)の値が返ります(図Math03-009)。なお、計算には円周率πや平方根が含まれますので、結果に誤差が生じることもあります。

var RADIAN_TO_DEGREE:Number = 180/Math.PI;
var nRadian:Number = Math.atan2(Math.sqrt(3), 1);
trace(nRadian);   // 出力: 1.0471975511965976
var nDegree:Number = nRadian*RADIAN_TO_DEGREE;
trace(nDegree);   // 出力: 59.99999999999999

○03-05 座標軸の方向について
最後に、座標軸の方向について、ひとつだけ確認しておきます。これまでy軸が上に正方向の数学的な直交座標で説明をしてきました。しかし、Flashなどコンピュータ画面上は、y軸の正方向は下向きです。すると、角度や座標の計算について、Flash上はどこか修正しなければならないでしょうか。

結論として、直交座標でさえあれば、数学上の考え方には何ら変わりはありません。数学のグラフ用紙をFlashでは上下逆さにして裏返したというだけのことです。角度や座標の計算の仕方は、まったく同じです。

違う点といえば、Flashではy座標を増やせば下向きに移動することと、回転の正方向が時計回りになるということだけでしょう。

[Prev/Next]

作成者: 野中文雄
作成日: 2008年1月14日