○02-01 三平方の定理とは
直角三角形の直角を挟んだ2辺の長さをaとb、直角に対する斜辺(もっとも長い辺)の長さをcとすると(図Math02-001)、つぎの等式が成立ちます。これを「三平方の定理」あるいは「ピタゴラスの定理」と呼びます。
【三平方の定理】
a2+b2 = c2
図Math02-001■三平方の定理

|
直角を挟んだ2辺の長さをaとb、斜辺の長さをcとする。
|
|
Maniac! Math02-001■ピタゴラスの定理
この等式自体は、ピタゴラス(ピュタゴラスとも呼ばれます)以前から知られていたようです。古代エジプトやインド、中国でも、この定理がすでに使われていたといいます。
しかし、定理を初めて数学的に証明したのが、ピタゴラスまたはその弟子だったとされています。もっとも、ピタゴラス本人についても、彼が弟子たちを集めて創った教団についても資料は少なく、その証明がどのようなものであったのかも定かではありません。
[*筆者用参考] 遠山啓『数学入門(上)』p.164-
|
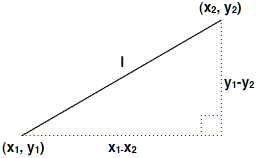
三平方の定理を使うと、2点間の距離を求めることができます。2点の座標をそれぞれ(x1, y1)および(x2, y2)とし、2点間を結ぶ直線を斜辺とした直角二等辺三角形を考えます(図Math02-002)。すると、直角二等辺三角形の底辺が(x1-x2)、高さが(y1-y2)になります。よって、2点間の長さをlとしたとき、三平方の定理より、つぎの等式が成立ちます。
l2 = (x1-x2)2+(y1-y2)2
l = ±√(x1-x2)2+(y1-y2)2
2点間の距離は正数ですので、つぎの式で表されます。
【2点(x1, y1)と(x2, y2)との距離l】
l = √(x1-x2)2+(y1-y2)2
図Math02-002■三平方の定理により2点間の距離を求める
|
斜辺をlとすると、直角を挟む2辺はそれぞれ(x1-x2)と(y1-y2)になる。
|
|
Tips Math02-001■円の方程式
円は、中心(a, b)からの距離が半径rに等しい任意の点(x, y)の集まりです。したがって、三平方の定理を使って、つぎの方程式で表されます(三角関数を使った円の方程式については後述Tips Math03-002「中心がC(a, b)で半径がrの円の方程式」参照)。
(x-a)2+(y-b)2 = r2
|
○02-02 三平方の定理の証明
三平方の定理の証明は数多く、それだけで本が1冊できるほどです。ここではその中から、直感的な方法とスタンダードな証明をひとつずつご紹介します。いずれも幾何学的な証明で、直角を挟む2辺a、bそれぞれと等しい1辺をもつふたつの正方形の面積の和(a2+b2)が、斜辺cに等しい1辺をもった正方形の面積c2に一致することを示します。
●図形の並べ替えによる直感的な証明
直角を挟む2辺の長さをa、b、斜辺をcとする直角二等辺三角形を4つ用意します。そして、この4つの直角二等辺三角形を、1辺が(a+b)の長さの正方形の上に並べます。
正方形の大きさは4つの直角二等辺三角形を合わせた面積より大きいので、並べた隙間に空き地ができます。しかし、どのように並べようとも、空き地の面積(=正方形の面積-直角二等辺三角形の面積×4)は一定のはずです。
まず、つぎの並べ方1(図Math02-003)では、ふたつの正方形の領域が空き地になります。それぞれの1辺は、aとbです。したがって、空き地の合計の面積は、つぎの式で求められます。
a2+b2
図Math02-003■並べ方1 ー ふたつの正方形の領域ができる

|
1辺がaとb、それぞれの正方形の領域が、合計ふたつ空き地になる。
|
それでは直角二等辺三角形の配置を変えて、つぎの並べ方2(図Math02-004)のようにしてみます。すると、1辺がcの四角い領域が空き地になります。四角の四隅の角度はすべて90度ですので(理由は、後述Tips Math02-002「三角形の内角の和は180度」参照)、これは正方形です。よって、空き地の広さは、この正方形の面積になります。
c2
図Math02-004■並べ方2 ー ひとつの正方形の領域ができる

初めに述べたとおり、並べ方1も並べ方2も、空き地の面積は同じでなければなりません。つまり、ふたつの空き地の面積は等しいので、つぎの等式が成立ちます。
a2+b2 = c2
|
Tips Math02-002■三角形の内角の和は180度
三角形の内角(3頂点それぞれの角度)の和は、180度であることが知られています。直角三角形は、そのうちのひとつの角が90度です。したがって、他の2角を足すと、90度になります。
前図並べ方2(図02-004)の1辺がcの四角形の角は、180度から直角三角形の直角でない2角を引いた角度です。つまり、その大きさは、90度(=180-90)になります。
三角形の内角の和が180度であることは、以下の図Math02-005で確かめることができます。補助線として底辺を一方に延ばし、その頂点から他方の辺と平行な直線を引いています。平行線と直線が交わったとき、「同位角」あるいは「錯角」がそれぞれ等しくなることを利用します。
図Math02-005■三角形の内角の和が180度であることを示す

|
底辺を一方に延ばし、さらにその頂点から他方の辺と平行な直線を引く。
|
|
●三角形の合同を使って面積を求めるスタンダードな証明
直角三角形のそれぞれの辺を1辺とする正方形を、合計3つ作図します(図Math02-006)。そして、直角三角形の直角の頂点から斜辺に対して垂線を延ばし、斜辺上に作成した1辺がcの正方形の領域を、XとYのふたつの長方形に分けます。
そのうえで、長方形Xの面積が1辺aの正方形に等しく、同じくYの面積が1辺bの正方形に等しいことを示せれば、三平方の定理は証明されます。
図Math02-006■直角三角形の各辺を1辺とする正方形の面積を比べる

|
直角三角形の各辺を1辺とする正方形を描き、直角三角形の直角の頂点から斜辺に延ばした垂線で、斜辺上の正方形をXとYのふたつの長方形に分ける。
|
まず、長方形Xと1辺がaの正方形について検討します(図Math02-007)。
直角三角形の直角の頂点Cと長方形Xの頂点Eを結んで、三角形ACEを作図します。この三角形の底辺を長さcのAEとすれば、高さはEFの長さです。したがって、三角形ACEの面積は同じAEとEFを2辺とする長方形Xの半分になります。
もうひとつ、直角三角形の頂点Bと1辺aの正方形の点Dとを結んで、三角形ADBをつくります。この三角形の底辺を長さaのADとすれば、高さは同じく長さaのACです。よって、三角形ADBの面積は1辺がaの正方形の半分になります。
図Math02-007■三角形ACEとADBを作図

|
三角形ACEの面積は長方形Xの半分で、三角形ADBの面積は1辺aの正方形の半分になる。
|
そして、三角形ACEとADBは、以下の条件により合同です(下記Tips Math02-003「三角形の合同条件」の2に合致)。したがって、ふたつの三角形の面積は等しく、それぞれの2倍である長方形Xと1辺aの正方形の面積もまた等しくなります。
(1) AC = AD = a
(2) AE = AB = c
(3) ∠CAE = ∠DAB = ∠BAC+90
|
Tips Math02-003■三角形の合同条件
ふたつの図形の形と大きさが同じであることを「合同」といいます。三角形が合同であるための条件は、以下の3つのうちのいずれかです。
【三角形の合同条件】
1. 三角形の対応する3組の辺がそれぞれ等しい。
2. 三角形の対応する2組の辺と、その間の角がそれぞれ等しい。
3. 三角形の対応する1組の辺と、その両端の角がそれぞれ等しい。
なお、最後の条件は、「三角形の内角の和は180度」(前掲Tips Math02-002)であることを考えれば、対応する1辺の「両端の角」であることは必要ありません。
|
|
Maniac! Math02-002■合同とは
「合同」とは、厳密にはつぎのように定義されます。
平面上のふたつの図形について、平行移動・回転移動・対称移動のみを用いることにより、すべての点が一致するように重ね合わせることができるとき、ふたつの図形は合同であるといいます。
|
つぎに、長方形Yと1辺がbの正方形についても、同様に面積は等しいことを示すことができます。
以上より、つぎのように三平方の定理が求められます。
長方形Xの面積 = a2
長方形Yの面積 = b2
長方形Xの面積+長方形Yの面積 = c2
a2+b2 = c2
作成者: 野中文雄
作成日: 2007年10月22日





