サイトトップ
Director Flash 書籍 業務内容 プロフィール

Adobe Flash CS3 Professional ActionScript 3.0

□Math 04 直線の式

直線は、直交座標のグラフに、一次関数として表すことができます。この一次関数(方程式)がどのように導かれるのか、そのポイントをご紹介します。

○04-01 直線を式で表す
直線は、x軸y軸の直交座標に、xのyに対する一次関数として、つぎのように表されます(図Math04-001)。

y = mx + n
図Math04-001■直線はxのyに対する一次関数として表される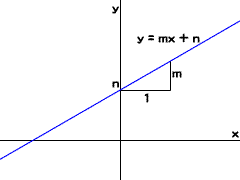

y切片がn、傾きmの一次関数。

上記の一次関数y = mx + nで、xが0のときyはnになります。つまり、y軸(x = 0)と値nの点で直線が交わります。この点を「y切片」といいます。yの値はxの値に比例し、m倍の割合で変化します。mは「yの値の変化/xの値の変化」で計算され、xの値が1増加したときyの値はm増加することを意味します。このmは直線の傾き具合を表すので、「傾き」と呼ばれます。


Tips Math04-001■一般化した直線の式
y = mx + nの式では、y軸に平行な直線x = aを表すことができません。したがって、直線はより一般的にはつぎの式で定義されます

ax + by + c = 0

しかし、y = mx + nの式の方が、傾きとy切片から直線の形状を把握しやすいので、広く使われています。

○04-02 指定された点を通る直線の式
指定された点を通る直線の式は、公式として暗記した覚えのある人が少なくないでしょう。けれど、1で述べた直線の一次関数式と傾きの考え方さえ理解すれば、公式はものの1、2分で導けます。つまり、丸覚えする必要はありません。また、考え方を理解する方が、応用範囲も広いといえます。

ポイントは、傾きを考えることです。それではまず、点A(x1, y1)を通る傾きmの直線を求めてみましょう。求める直線上の任意の点をP(x, y)とします。すると、この直線の傾きは、つぎの式で計算できます。

傾き = yの値の変化/xの値の変化 = (y - y1)/(x - x1)

直線の傾きは一定ですので、この値はmに等しくなければなりません。したがって、つぎの方程式が成立ちます。

(y - y1)/(x - x1) = m
y - y1 = m (x - x1)
y = m (x - x1) + y1

点P(x, y)は、直線上の任意の点としました。逆にいえば、この式を満たす(x, y)の集まりが、直線を構成するということになります。つまり、この式が求める直線の方程式です。

Tips Math04-002■1点と傾きを指定した直線の式
点(x1, y1)を通る傾きmの直線は、以下の式で表されます。

y = m (x - x1) + y1

つぎに、2点を通る直線の式を考えてみます。2点をA(x1, y1)とB(x2, y2)とします。第1に、点Aを通る訳ですから、直線上の任意の点をP(x, y)としたとき、前述の1点を通る直線(Tips Math04-002)を求めるときと同じ傾きの式が導けます。

傾き = (y - y1)/(x - x1)

第2に、点Aと点Bから、傾きが求められます。

傾き = (y1 - y2)/(x1 - x2)

これらふたつの傾きは、同じ直線の値ですから、当然等しくなければなりません。したがって、以下の方程式が成立ちます。

(y - y1)/(x - x1) = (y1 - y2)/(x1 - x2)
y - y1 = (y1 - y2) (x - x1)/(x1 - x2)
y = (y1 - y2) (x - x1)/(x1 - x2) + y1

Tips Math04-003■指定した2点を通る直線の式
2点(x1, y1)および(x2, y2)を通る直線は、以下の式で表されます。

[*イラスト候補●Math04-001] 傾きを考えることがポイントだね。


○04-03 直交する直線
ふたつの直線が垂直に交わる場合、一方の直線の傾きをmとすると、もう一方の直線の傾きは-1/mとなります。つまり、ふたつの直線の傾きの積は、-1になります。

Tips Math04-004■ふたつの直線が垂直に交わる条件
傾きmの直線と傾きm'の直線が垂直に交わるとき、つぎの関係が成立ちます。ただし、傾きm≠0とします。

m・m' = -1

あるいは

m' = -1/m

このふたつの直線の傾きの関係は、つぎのように図形的に説明することができます(図Math04-002)。

図Math04-002■直交する2直線の傾き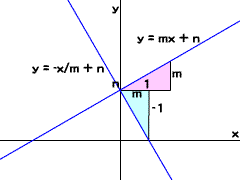

傾きがそれぞれmと-1/mの2直線は直交する。

傾きがmの直線は、xの値が1変化すると、yの値はm変化します。傾きが-1/mの直線は、xの値がm変化すると、yの値が-1変化することになります。このふたつの直線の傾きを示した上図Math04-002において、【ピンク】と【水色】のふたつの直角三角形は、合同になります。直角を挟む2辺の長さが、それぞれ1とmとなっており、互いに等しいからです。

[編集者用注釈]【ピンク】と【水色】は、図Math04-002の表現方法によって変更します。

三角形の内角の和は、180度です。したがって、直角三角形の(直角でない)2鋭角の和は、90度になります。上図Math04-002で、ふたつの直線の交点は、合同な(【ピンク】と【水色】の)ふたつの直角三角形の異なる2鋭角が合わさった角度を成しています。つまり、2直線は直角に交わっているということです。

Tips Math04-005■直行条件をベクトルで示す
傾きがmの直線と傾きが-1/mの直線とが直交することは、ベクトルを使って説明することもできます。ベクトルA(1, m)とベクトルB(m, -1)とは、それぞれふたつの直線と傾きが一致します(図Math04-003)。

図Math04-003■直交する2直線のベクトルで表された傾き

直行するベクトルは、内積が0。

ふたつのベクトルが直交する条件は、内積が0になることです。ベクトルAとベクトルBとの内積は、つぎのように計算されます。

A・B = AxBx + AyBy = 1m + m(-1) = m - m = 0

したがって、ベクトルAとベクトルBとは直交し、これらのベクトルと傾きの等しいふたつの直線も同じように直交します。

[Prev/Next]

作成者: 野中文雄
作成日: 2008年7月15日
Copyright © 2001-2008 Fumio Nonaka.  All rights reserved.