Matrixクラスを使うと、DisplayObjectインスタンスの2次平面上の移動や伸縮、回転、傾斜などの変形ができます。長方形のインスタンスを平行四辺形に変えることができますので、3次元の表現に利用することも可能です。
○05-01 Matrixクラスが表す変換行列
Matrixクラスは、2次元の座標空間を別の2次元の座標空間に変換する3行×3列の行列で表されます。この行列は「変換行列」とか「変換マトリックス」(transformation matrix)と呼ばれます。
●Matrixクラスのメソッドによる変換の操作
DisplayObjectインスタンスの座標空間をコントロールするMatrixオブジェクトは、DisplayObject.transformプロパティからmatrixプロパティ(Transform.matrixプロパティ)を参照して操作することができます。Matrixオブジェクトにより、DisplayObjectインスタンスのxy座標の平行移動や拡大・縮小、回転、傾斜などの処理が行えます。
|
Tips Tech05-001■アフィン変換
Matrixクラスが行う座標空間の変換を、「アフィン変換」といいます。アフィン変換では、もとの座標空間で平行な2直線は、変換後も平行になります。つまり、長方形をパース(09-05「重ね順と遠近法」参照)のかかった台形に変形することはできません。
|
Matrixクラスには、オブジェクトの移動や伸縮、回転などを適用するメソッドが用意されています。メソッドの引数や戻り値、その処理内容は下表Tech05-001のとおりです。
表Tech05-001■Matrixクラスの座標変換を適用するメソッド
|
メソッド
|
説明
|
|
translate(ピクセル数x:Number, ピクセル数y:Number):void
|
変換行列に、x軸とy軸方向それぞれについて、引数で指定されたピクセル数の平行移動を設定します。
|
|
scale(伸縮率x:Number, 伸縮率y:Number):void
|
変換行列に、x軸とy軸方向それぞれについて、引数で指定された小数値の比率の拡大・縮小を設定します。
|
|
rotate(回転角:Number):void
|
変換行列に、引数で指定されたラジアン角の回転を設定します。
|
DisplayObjectインスタンスに対して、Matrixクラスの上記メソッドや変換行列を適用する手順はつぎのとおりです。
【Matrixインスタンスを使ったDisplayObjectインスタンスの変換の手順】
- DisplayObject.transformプロパティのmatrixプロパティからMatrixインスタンスを取得する。
または
new演算子でMatrixコンストラクタを呼出して新規Matrixインスタンスを生成する。
- Matrixのメソッドや変換行列のプロパティ(後述)によりMatrixインスタンスを変換する。
- 変換の処理が加えられたMatrixインスタンスをDisplayObject.transformプロパティのmatrixプロパティに設定する。
たとえば、タイムラインに配置されたMovieClipインスタンスmy_mcに対し、(1)水平方向に1.5倍、垂直方向に1.2倍拡大し、(2)時計回りに30度(= π/6ラジアン)回転して、(3)x座標を80ピクセル、y座標を40ピクセル移動するには、つぎのようなフレームアクションを記述します。なお、trace()関数は、変換行列の情報を[出力]します(変換行列については、このあと詳しく説明します)。
var myMatrix:Matrix = my_mc.transform.matrix;
trace(myMatrix);
myMatrix.scale(1.5, 1.2);
trace(myMatrix);
myMatrix.rotate(Math.PI/6);
trace(myMatrix);
myMatrix.translate(80, 40);
trace(myMatrix);
my_mc.transform.matrix = myMatrix;
MovieClipインスタンスmy_mcの基準点が左上隅にあり、タイムラインの基準点(メインタイムラインでしたら左上隅)に配置してあったとすると、上記スクリプトにより図Tech05-001左図のようにインスタンスが変換されます(各メソッドが適用された経過のインスタンスの状態も示してあります)。ここで、注意しておきたいことが、ふたつあります。
第1は、Matrixインスタンスを適用するためには、DisplayObject.transformプロパティのmatrixプロパティに、必ず変換後のMatrixインスタンスを代入しなければならないということです。Matrixインスタンスは、もちろん参照渡しです。しかし、DisplayObject.transformプロパティのmatrixプロパティで取得したMatrixインスタンスを操作しても、それだけではDisplayObjectインスタンスに変換は適用されません。
第2に、Matrixインスタンスの変換は、DisplayObjectインスタンスがもともと配置されていた座標空間の基準点を原点として行われます。したがって、Matrixクラスのメソッドに同じ引数を渡したとしても、その適用の順序によって変換結果が変わります。たとえば、上記フレームアクションでMatrix.translateメソッドを変換処理の最初に移動すると、変換結果は図Tech05-001右図のようになります。
インスタンスが移動しても座標空間の原点は動きませんので、つぎにインスタンスを拡大したとき、大きさが変わるだけでなく原点からインスタンスの距離も変化します。また、続く回転も原点を中心として行われることになるからです。
図Tech05-001■MovieClipインスタンスにMatrixクラスのメソッドを適用
|
Matrix.scaleとMatrix.rotate、Matrix.translateの各メソッドの適用順序によって、インスタンスの変換結果は異なる。
|
●変換行列とその要素
前述のMatricクラスのメソッドを使うと、Matrixインスタンスを取得・設定する以外、とくに変換行列というものを意識しなくても済みました。しかし、必要があれば、変換行列の内容を直接操作することもできます。ただその前に、変換行列を用いる意義について、確かめておきます。
Matrix.scaleやMatrix.rotate、Matrix.translateの各メソッドで行った拡大・縮小、回転、座標の移動といった操作は、DisplayObjectクラスのプロパティDisplayObject.scaleX/DisplayObject.scaleYやDisplayObject.rotation、DisplayObject.x/DisplayObject.yを使って処理することもできました。では、わざわざMatrixクラスを使うと、何がよくなるのでしょう。ここでは、ふたつ挙げておきます。
第1は、インスタンスに対する内容の異なった操作が、変換行列というひとつの処理で行えることです。たとえば、数多くのインスタンスに同じ変換を行いたいという場合、変換用のMatrixインスタンスをひとつつくっておけば、それをDisplayObject.transformプロパティのmatrixプロパティに設定するだけで済みます。また、複数の変換行列を組合わせて適用することにより、複雑な変換を行うこともできます。
第2に、変換行列を操作することにより、傾斜の変換が可能になります。つまり、長方形を平行四辺形にゆがめることができるのです。これは、3次元空間の平面を表現するのに役立ちます。なお、傾斜を行うメソッドはMatrixクラスには用意されていません。変換行列を直接操作する必要があります。
そこで、変換行列がどういうものかをご説明していきます。Matrixインスタンスを表す変換行列は、3行×3列の数学的な行列です。行列の各要素(「成分」とも呼ばれます)は、プロパティとして以下のように定義されています。なお、変換行列の最後の行は、Matrixクラスでは要素が固定されており、操作対象にはなりません。

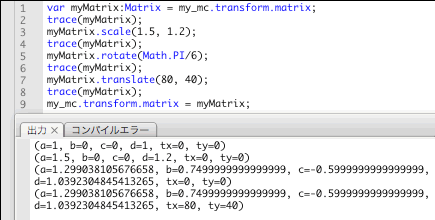
前掲のフレームアクションにはtrace()関数を挿入して、各メソッド適用前後のMatrixインスタンスつまり変換行列の情報を[出力]しました。そこには、変換行列の各要素つまりプロパティの値が表示されています(図Tech05-002)。それでは、それらのプロパティが、変換行列を適用したインスタンスにどのような変化を与えるのか、下表Tech05-002に簡単にまとめます。前掲表Tech05-001でご紹介したMatrixクラスの対応するメソッドも、併せて掲載しました。
図Tech05-002■Matrixインスタンスの[出力]は変換行列のプロパティ値を示す
|
Matrixクラスの各メソッドを適用する前後の変換行列の各プロパティ値が[出力]されている。
|
表Tech05-002■変換行列のプロパティ値とその適用結果
|
変換
|
メソッド
|
変換行列の値
|
変換結果
|
|
平行移動
|
translate(ピクセル数x:Number, ピクセル数y:Number):void
|

|

|
|
拡大・縮小
|
scale(伸縮率x:Number, 伸縮率y:Number):void
|

|

|
|
回転
|
rotate(θ:Number):void
|

|

|
|
傾斜
|
−
|

|

|
|
デフォルト
|
new Matrix()
|

|

|
|
Tips Tech05-002■[ヘルプ]のMatrixクラスの説明における変換行列の誤り
[ヘルプ]でMatrixクラスの説明を見ると、変換行列の記載で要素となるbとcのプロパティの位置が入れ違っています(表Tech05-003)。正しくは上記の表Tech05-002に掲載した変換行列のとおりです。
表Tech05-003■[ヘルプ]で誤って掲載されている変換行列
|
|
Tips Tech05-003■行列はパラメータの設定パネルのようなもの
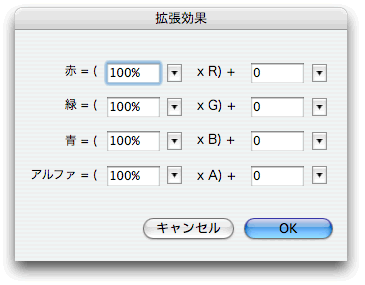
数学的な行列というと、途端にむずかしく感じる人も少なくないでしょう。しかし、行列というのは、一定の決まりに則った変数値が、規則的に並べられたものです。イメージでいえば、パラメータの並んだ設定パネルやダイアログボックスと似ています(図Tech05-003)
図Tech05-003■インスタンスのカラースタイルの[拡張効果]ダイアログボックス
|
インスタンスのカラーについて、赤(R)緑(G)青(B)アルファの各チャネルごとにパラメータを設定できる。
|
とくにフィルタのパラメータなどは、内部的にどのような処理が行われているのかまで理解している人はまれです。けれど、どのパラメータをどう動かすとどういう変化が起こるということさえ知っていれば、フィルタは充分利用できます。行列も同じように、各要素の値が結果にどのような影響を与えるかをつかんでおけば、基本的にはこと足ります。
もちろん、数学的な内容まで理解すれば、応用力は高まります。行列の基本については、数学編で解説します。
|

行列は、パラメータを決まりにしたがって並べたもの。
|
[*筆者用参考] senocular.com「Understanding the Transformation Matrix in Flash 8」。
●長方形を平行四辺形に変換する
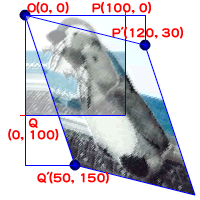
変換行列の4つの要素、プロパティa、b、c、dを使うと、長方形が平行四辺形に変えられます。たとえば、左上隅を基準点とする1辺100ピクセルの正方形のインスタンスをタイムラインの基準点O(0, 0)に配置したとします(図Tech05-004)。そして、右上隅の点P(100, 0)をP'(120, 30)に、左下隅の点Q(0, 100)をQ'(50, 150)に変換して、平行四辺形にするにはつぎのように4つのプロパティ値を計算します。
Matrix.a: P'のx座標値/Pのx座標値 = 120/100 = 1.2
Matrix.b: P'のy座標値/Pのx座標値 = 30/100 = 0.3
Matrix.c: Q'のx座標値/Qのy座標値 = 50/100 = 0.5
Matrix.d: Q'のy座標値/Qのy座標値 =150/100 = 1.5
以上の計算されたプロパティ値を変換行列に適用し、タイムラインに配置したMovieClipインスタンスmy_mcを変換するには、つぎのようなフレームアクションを記述します。その結果インスタンスは、もちろん目的とした下図Tech05-004のとおりに変換されます。
var myMatrix:Matrix = my_mc.transform.matrix;
myMatrix.a = 1.2;
myMatrix.b = 0.3;
myMatrix.c = 0.5;
myMatrix.d = 1.5;
my_mc.transform.matrix = myMatrix;
図Tech05-004■変換行列により長方形を平行四辺形に変換する
|
変換行列(Matrixインスタンス)に対してMatrix.a、Matrix.b、Matrix.c、Matrix.dの4つのプロパティ値を設定することにより、長方形を平行四辺形に変換することができる。
|
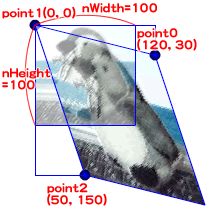
それでは、この長方形を平行四辺形に変換する処理を、クラスの静的(staticな)メソッドとして定義してみましょう。クラスはMathUtilsと名づけ、静的メソッドはtransformPoints()として5つの引数を与えて定義します。まず、最初のふたつの引数(nWidthとnHeight)は、もとの長方形のそれぞれ右上隅(図Tech05-005のnWidth)のx座標値と左下隅(同nHeight)のy座標値です。残りの3つの引数(point0、point1、point2)はいずれも変換後の座標を示すPointインスタンスで、順に右上隅の座標(同point0)、左上隅の座標(同point1)、および右下隅の座標(同point2)となります。なお、静的メソッドtransformPoints()の戻り値は、変換行列(Matrixインスタンス)です。
package {
import flash.geom.Matrix;
import flash.geom.Point;
public class MathUtils {
public function MathUtils() {}
public static function transformPoints(nWidth:Number, nHeight:Number, point0:Point, point1:Point, point2:Point):Matrix {
// 処理内容を記述
}
}
}
図Tech05-005■MathUtilsクラスの静的メソッドtransformPoints()の引数として渡す値
|
静的メソッドMathUtils.transformPoints()は、ふたつの数値(Number型)と3つのPointインスタンスの計5つの引数を渡して、MathUtils.transformPoints(nWidth, nHeight, point0, point1, point2)のように呼出す。
|
この静的メソッドMathUtils.transformPoints()を使って、たとえば上図Tech05-005のように長方形を平行四辺形に変換するには、つぎのようなフレームアクションを記述することになります。
var nWidth:Number = my_mc.width;
var nHeight:Number = my_mc.height;
var point0:Point = new Point(120, 30);
var point1:Point = new Point(0, 0);
var point2:Point = new Point(50, 150);
my_mc.transform.matrix = MathUtils.transformPoints(nWidth, nHeight, point0, point1, point2);
以上の仕様にもとづいてMathUtilsクラスと静的メソッドtransformPoints()を定義したのが、つぎのスクリプトTech05-001です。静的メソッド本体ではPoint.subtract()メソッドを使っています。このメソッドは、引数のPointインスタンスが原点(0, 0)だとしたとき、ターゲットのPointインスタンスのxy座標値がいくつになるかを計算し、そのxy座標値のPointインスタンスを返します。つまり、引数のPointインスタンスの座標から見た、ターゲットのPointインスタンスの相対座標をもったPointインスタンスが返されます。
たとえば、ふたつのPointインスタンスpoint0とpoint1が、それぞれxy座標(20, 10)と(140, 70)をもつとします。そのとき、point1.subtract(point0)は、xy座標が(120, 60)となるPointインスタンスを返します(図Tech05-006)。
図Tech05-006■ふたつのPointインスタンスの座標と一方から見た他方の相対座標

|
Pointインスタンスpoint0(20, 10)を原点(0, 0)とみなすと、point1(140, 70)の相対座標は(120, 60)になる。
|
|
Tips Tech05-004■Point.subtract()メソッドの意味
"subtract"は、引き算を意味します。実際、Point.subtract()メソッドは、ターゲットと引数のふたつのPointインスタンスのxy座標を引き算して、その値を戻り値のPointインスタンスに設定します。つまり、つぎのふたつのステートメントは、xy座標値が同じPointインスタンスを返します。
point1.subtract(point0)
new Point(point1.x-point0.x, point1.y-point0.y)
なお、この計算はベクトルの引き算として定義されます(数学編第05章「ベクトル」参照)。
|
スクリプトTech05-001■長方形を平行四辺形に変換する静的メソッドMathUtils.transformPoints()
|
// ActionScript 3.0クラス定義ファイル: MathUtils.as
package {
import flash.geom.Matrix;
import flash.geom.Point;
public class MathUtils {
public function MathUtils() {
}
public static function transformPoints(nWidth:Number, nHeight:Number, point0:Point, point1:Point, point2:Point):Matrix {
var myMatrix:Matrix = new Matrix();
var point1_0:Point = point0.subtract(point1);
var point1_2:Point = point2.subtract(point1);
myMatrix.tx = point1.x;
myMatrix.ty = point1.y;
myMatrix.a = (point1_0.x)/nWidth;
myMatrix.b = (point1_0.y)/nWidth;
myMatrix.c = (point1_2.x)/nHeight;
myMatrix.d = (point1_2.y)/nHeight;
return myMatrix;
}
}
}
|
transformPoints()メソッドの第4引数にインスタンスの左上隅の座標をPointインスタンスで渡すようにしたのは、原点(0, 0)以外のxy座標値を与え、インスタンスを平行移動できるようにするためです。たとえば、前掲のフレームアクションと同じように、タイムラインに配置したインスタンスmy_mcを平行四辺形に変換したうえで(図Tech05-005)、さらにxy座標を(40, 20)平行移動するには、つぎのようにスクリプトを書替えます。
var nWidth:Number = my_mc.width;
var nHeight:Number = my_mc.height;
var point0:Point = new Point(160, 50);
var point1:Point = new Point(40, 20);
var point2:Point = new Point(90, 170);
my_mc.transform.matrix = MathUtils.transformPoints(nWidth, nHeight, point0, point1, point2);
図Tech05-007■インスタンスを平行四辺形に変換して平行移動する

|
前掲フレームアクションと同じようにインスタンスを平行四辺形に変換したうえで(図Tech05-005)、さらにxy座標を(40, 20)平行移動する。
|
MathUtils.transformPoints()メソッドを定義した前掲スクリプトTech05-001では、この平行移動を加えたため、前準備の処理があります。新規のMatrixインスタンスを生成したあと、基準点となる第4引数point1から見た第3および第4引数point0およびpoint2の相対座標をそれぞれPoint.subtract()により算出しています。続く、変換行列の要素であるMatrixクラスのインスタンスの設定については、すでにご説明したとおりです。
さて、このMathUtils.transformPoints()メソッドを使えば、いかなる長方形も任意の平行四辺形に変換できます。そこで簡単なサンプルスクリプトをつくってみましょう。長方形(正方形)インスタンスの3つの角にドラッグ可能なポイントのインスタンスを配置し、それを自由に移動すると長方形がそのポイントに合わせて平行四辺形に変形するというものです(図Tech05-008)。
図Tech05-008■ドラッグした3つの角のポイントに合わせてインスタンスが変形

|
長方形のインスタンスの3つの角にあるポイントをドラッグすると、それに合わせてインスタンスが平行四辺形に変形する。
|
メインタイムラインに長方形の変形させるインスタンスmy_mcと、その3つの角にポイントにするインスタンスを配置します。ポイントのインスタンス名は、右上隅がpoint0_mc、左上隅はpoint1_mc、左下隅をpoint2_mcとします(上図Tech05-008)。なお、ポイントの3つのインスタンスはひとつのMovieClipシンボルから作成し、シンボルの基準点を中央に設定しておきます。
簡易なサンプルにするため、インスタンスmy_mcを変換するスクリプトは、メインタイムラインのフレームアクションとしてつぎのように記述することにします(スクリプトTech05-002)。
スクリプトTech05-002■長方形のMovieClipインスタンスを任意の平行四辺形に変換する
|
// タイムライン: メイン
// 第1フレームアクション
function xTransform():void {
var point0:Point = new Point(point0_mc.x, point0_mc.y);
var point1:Point = new Point(point1_mc.x, point1_mc.y);
var point2:Point = new Point(point2_mc.x, point2_mc.y);
xTransformMovieClipPoints(my_mc, point0, point1, point2);
}
function xTransformMovieClipPoints(_mc:MovieClip, point0:Point, point1:Point, point2:Point):void {
_mc.transform.matrix = new Matrix(); // matrixプロパティにデフォルトのMatrixインスタンスを設定
// もとのMovieClipインスタンスの幅と高さを取出す
var nWidth:Number = _mc.width;
var nHeight:Number = _mc.height;
// 取得した値を引数にしてMathUtils.transformPoints()メソッドを呼出す
_mc.transform.matrix = MathUtils.transformPoints(nWidth, nHeight, point0, point1, point2);
}
|
スクリプトTech05-002の関数xTransform()は、ポイントの3つのインスタンスからxy座標を取出してPointインスタンスにしたうえで、変換するインスタンスmy_mcと3つのPointインスタンスを引数として、もうひとつの関数xTransformMovieClipPoints()を呼出しています(図Tech05-009)。
関数xTransformMovieClipPoints()の基本的な処理は、変換対象のMovieClipインスタンスからもとの幅と高さを調べ、そのふたつの値と引数で受取ったPointインスタンス3つをMathUtils.transformPoints()メソッドに渡します。そして、メソッドから返された変換行列(Matrixインスタンス)をMovieClipインスタンスのDisplayObject.transformプロパティのmatrixプロパティ(Transform.matrixプロパティ)に設定すれば、インスタンスが変換されます。
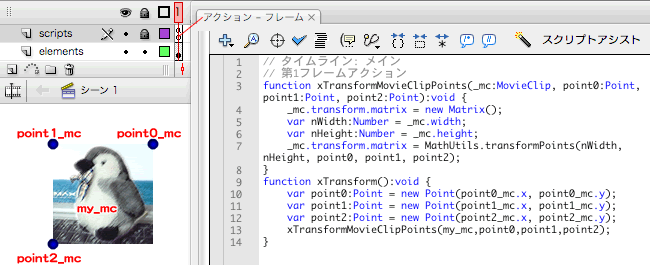
図Tech05-009■3つのポイントの座標値からMovieClipインスタンスを変換するフレームアクション
|
3つのポイントのインスタンスの座標値と、長方形(正方形)のインスタンスのプロパティ値から引数値を計算し、MathUtils.transformPoints()メソッドの呼出しにより、MovieClipインスタンスを平行四辺形に変換する。
|
ここで注意しなければならないのは、これらの関数は何度も呼出されて、MovieClipインスタンスに繰返し変換を加えることになるという点です。しかし、関数xTransformMovieClipPoints()の本体から、MathUtils.transformPoints()メソッドに引数として渡すべきもとのインスタンスの幅と高さは、変換する前のMovieClipインスタンスの値でなければなりません。そのため、インスタンスのDisplayObject.transformのmatrixプロパティに、Matrixクラスのコンストラクタから生成したデフォルトのMatrixインスタンス(前掲表Tech05-002参照)を設定して、初期状態の幅と高さの値を得ています。
このサンプルであと残るスクリプトは、ドラッグするポイントのMovieClipシンボルに記述するフレームアクションです(図Tech05-010)。このフレームアクション(スクリプトTech05-003)の構成は、前章04-05「親子によるイベントの連携処理」で作成したスクリプトTech04-006と基本的に同じです。ただし、今回のスクリプトTech05-003では、マウスボタンを放すのがMovieClipインスタンス上でも、その外であっても処理は変わりませんので、インスタンスとStageオブジェクトのInteractiveObject.mouseUpイベント(定数MouseEvent.MOUSE_UP)に同じリスナー関数を登録しています。
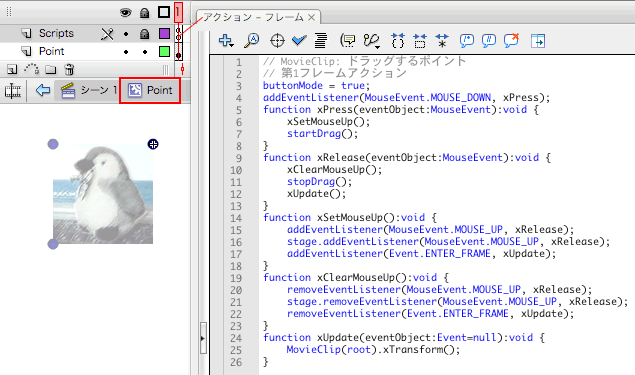
図Tech05-010■ドラッグするポイントのMovieClipシンボルにフレームアクションを記述
|
構成の基本は、前章のスクリプトTech04-006と同じ。ただし、マウスボタンを放したときの処理は、インスタンス上でもその外でも同じリスナー関数。
|
スクリプトTech05-003■ポイントのMovieClipに記述するフレームアクション
|
// MovieClip: ドラッグするポイント
// 第1フレームアクション
buttonMode = true;
addEventListener(MouseEvent.MOUSE_DOWN, xPress);
function xPress(eventObject:MouseEvent):void {
xSetMouseUp();
startDrag();
}
function xRelease(eventObject:MouseEvent):void {
xClearMouseUp();
stopDrag();
xUpdate();
}
function xSetMouseUp():void {
addEventListener(MouseEvent.MOUSE_UP, xRelease);
stage.addEventListener(MouseEvent.MOUSE_UP, xRelease);
addEventListener(Event.ENTER_FRAME, xUpdate);
}
function xClearMouseUp():void {
removeEventListener(MouseEvent.MOUSE_UP, xRelease);
stage.removeEventListener(MouseEvent.MOUSE_UP, xRelease);
removeEventListener(Event.ENTER_FRAME, xUpdate);
}
function xUpdate(eventObject:Event=null):void {
MovieClip(root).xTransform();
}
|
今回新たに使うメソッドは、Sprite.startDrag()とSprite.stopDrag()です。前者のメソッドを呼出すと、それ以降インスタンスはマウスポインタを追いかけて移動します。後者は、前者のメソッドを終了して、インスタンスの動きを止めます。つまり、これらふたつのメソッドは、ドラッグの開始と終了に用いられます。
|
Tips Tech05-005■Sprite.startDrag()メソッド
Sprite.startDrag()メソッドを[ヘルプ]で調べると、「指定されたスプライトをユーザーがドラッグできるようにします」と説明されています。「ドラッグ」とは、マウスボタンを押したままマウスを移動することです。しかし、Sprite.startDrag()は、本文に解説したとおり、インスタンスをマウスポインタに追随させるメソッドです。つまり、マウスボタンを押しているかどうかは関係がありません。
また、Sprite.startDrag()メソッドは、1度にひとつのインスタンスしか制御できません。複数のインスタンスに対してこのメソッドを呼出すと、最後のインスタンスのみがマウスポインタに追随します。同時に複数のインスタンスを動かしたいときは、第04章「MovieClipの座標の操作」でご紹介したマウスポインタの座標に合わせてインスタンスを移動させる手法が考えられます。
|
ポイントのMovieClipインスタンスをクリック(InteractiveObject.mouseDownイベント発生)すると、関数xSetMouseUp()が呼出され、またSprite.startDrag()メソッドによりインスタンスがドラッグされます。関数xSetMouseUp()では、マウスボタンを放す操作(InteractiveObject.mouseUpイベント発生)の待受けとともに、インスタンスのDisplayObject.enterFrameイベントにリスナー関数xUpdate()を登録します。
関数xUpdate()は、メインタイムラインのフレームアクションに定義した関数xTransform()を呼出します。なお、メインタイムラインを参照するDisplayObject.rootプロパティは、戻り値の型がDisplayObjectクラスになります。DisplayObjectインスタンスには、MovieClipインスタンスのようにユーザーが自由に変数や関数を設定することができません。したがって、フレームアクションで宣言・定義された変数や関数にアクセスするためには、戻り値をMovieClipクラスでキャスト(Tips 10-012「キャスト」参照)する必要があります。
|
Tips Tech05-006■DisplayObject.rootプロパティからタイムラインの変数・関数を参照する
MovieClipやObjectクラス(06-06「Objectインスタンスの配列を使う」参照)のインスタンスには、変数(プロパティ)あるいは関数(メソッド)が自由に加えられます。このようなクラスを、dynamicなクラスといいます。
しかし、他の通常のクラスでは、予め定義されているプロパティとメソッド以外は設定も参照もできません。そのためdynamicでないクラスであるDisplayObject型が指定されたDisplayObject.rootプロパティを参照して、DisplayObjectクラスにない変数・関数にアクセスしようとすると[コンパイルエラー]が生じます。
図Tech05-011■DisplayObject.rootプロパティからタイムラインの変数・関数は直接参照できない
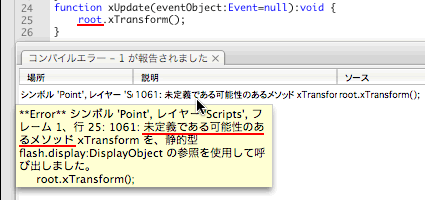
|
DisplayObjectはdynamicなクラスではないので、予め定義されているプロパティやメソッド以外にアクセスすると[コンパイルエラー]になる。
|
しかし、DisplayObject.rootプロパティの戻り値がタイムラインであれば、MovieClipクラスでキャストすることにより、そこに宣言した変数や定義した関数にアクセスできるようになります(詳しくは、FumioNonaka.com「rootプロパティでメインタイムラインの関数にアクセスできない」<http://www.fumiononaka.com/TechNotes/Flash/FN0707001.html>参照)。
|
インスタンスのDisplayObject.enterFrameイベントに登録されたリスナー関数xUpdate()は、インスタンスがドラッグされている間継続して呼出されます。そして、関数本体からメインタイムラインの関数xTransform()を呼出すことにより、インスタンスの形状を変換し続けることになります。
マウスボタンを放すと、関数xRelease()が呼出されます。この関数本体は、Sprite.stopDrag()メソッドによりインスタンスのドラッグを終了し、関数xClearMouseUp()とxUpdate()を呼出します。xClearMouseUp()関数は、マウスボタンを放す操作の待受けを終了するとともに、インスタンスのDisplayObject.enterFrameイベントに登録したリスナー関数xUpdate()を削除します。関数xRelease()からxUpdate()を呼出しているのは、マウスボタンを放した時点での変換を、最後に念のため適用するものです。
|
Tips Tech05-007■インスタンス外でのInteractiveObject.mouseUpイベント
Sprite.startDrag()メソッドでインスタンスを移動させているのであれば、インスタンス外でマウスボタンを放すという操作はありえないと思われるかもしれません。しかし、ユーザーが素早くマウスを動かしたとき、インスタンスがマウスポインタに追いつけず、その瞬間にマウスボタンを放す場合があり得ます。ですから、ドラッグ&ドロップなどのスクリプトを書くときには、インスタンス外でマウスボタンを放した場合の処理は念のため入れておくべきでしょう。
|
[ムービープレビュー]で確かめると、3つのポイントのドラッグに合わせてインスタンスの形状が変化します。
図Tech05-012■3つのポイントの位置に合わせてインスタンスに変換行列を適用

|
3つのポイントのインスタンスをドラッグすると、その位置に合わせた変換行列が適用され、インスタンスの形状が変換される。
|
○05-02 3次元の回転を表現する
前節で、長方形を任意の平行四辺形に変形しました。このテクニックを応用すれば、6つの長方形(正方形)の面からなる立方体を、3次元空間で回転させる表現が可能になります(図Tech05-013)。3次元空間の扱いを細かく解説するのはこの章の目的ではなく、また紙幅もかぎられていますので、その回転を中心に簡単にポイントとスクリプトのサンプルをご紹介することにします。
図Tech05-013■頂点座標に合わせて変換した平行四辺形を組合わせると3次元空間の立方体が表現できる

|
回転する頂点の座標を計算したうえで、正方形の画像を平行四辺形に変換して組合わせれば、3次元空間の立方体が表現できる。
|
|
Maniac! Tech05-001■パースをかける
前述(Tips Tech05-001「アフィン変換」)のとおり、変換行列を使った手法では、長方形は平行四辺形にしか変換できず、パースのかかった台形などの形状にはなりません。
しかし、長方形を複数の三角形に分け、そのそれぞれに傾斜などの変換を加えたうえで、それらの三角形を組合わせることにより平行四辺形以外の形状に見せることは可能です。
|
●ひとつの面を3次元で回転させる
いきなり6面つくるのでなく、まずはひとつの面を作成して、3次元空間で回転する表現を作成しましょう。スクリプトは、つぎの4つのパートで構成されます。
- MathUtilsクラス: 3点の座標に合わせた変換行列を計算する。
- Sprite3Dクラス: 立方体の各面を作成。対応する頂点の情報をもち、3頂点の座標に合わせたインスタンスの変換を行う。
- Point3Dクラス: 3次元座標をもち、その座標を3次元空間で回転させる。
- フレームアクション: 3つのクラスを用いて立方体を構成し、その座標の回転に合わせて2次元平面への変換を行う。
第1に、前節で定義したクラスMathUtilsは、とくに追加も修正もなく、そのまま利用します。第2のクラスSprite3Dは、Spriteクラスを継承し、画像を取込んで立方体の面をつくります。立方体においてその面が対応する頂点の情報をもたせるとともに、前掲フレームアクション(スクリプトTech05-002)で作成した関数xTransformMovieClipPoints()を、クラスのメソッドとして定義し直します。第3は、Point3Dクラスで、3次元座標をプロパティとしてもち、その座標を3次元空間で回転させるメソッドrotate()を備えます。
最後のフレームアクションは、3つのクラスを用いて立方体を構成し、その回転とそれに合わせた座標計算、面をつくる各インスタンスの変換などを行います。初めに述べたとおり、当面はひとつの面(インスタンス)で処理を作成します。それが正しく動作することを確かめたら、6面の立方体へと展開する予定です。
3次元空間の処理で、変換行列や座標の数学的な計算と負けず劣らず大切なのが、頂点と座標および各平面の位置と順序を正しく扱うことです。前節で確かめたとおり、長方形は3つの角の座標により、変換する平行四辺形の形状が指定できました。すると、同じように、立方体は6つの角の座標を定めれば、3次元空間における各面の変換が決まることになります(図Tech05-014左図)。
また、今回のサンプルでは3次元空間の原点(0, 0, 0)を、立方体の中心に置きます。つまり、3次元のx軸y軸z軸は、立方体の中心で直行します。Flashの座標系に合わせて、y軸は下方向を正とします。また、z軸は奥を正方向と定めます。すると、たとえば立方体の1辺を2とすると、各頂点の座標は下図Tech05-014右図のようになります。
図Tech05-014■立方体の頂点と座標を正確に管理する
|
立方体の6頂点で、各面は定まる。原点を立方体の中心に置くと、頂点の座標が決まる。
|
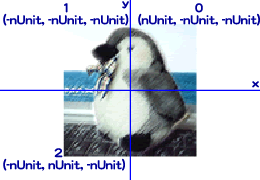
初めに試す1面は、立方体の前面にします。頂点には、右上隅(0)から左上隅(1)、左下隅(2)の反時計回りの順に番号をつけます(図Tech05-015)。前述のとおり、この頂点番号の順序は大切です。たとえば、あとで各面が立方体の前面か背面かを判別するときに、3頂点の位置関係が反時計回りになっているかどうかを調べたりします。なお、辺の長さについては、その半分の値を変数nUnitに設定します。すると、前面のz座標は-nUnitですので、3つの頂点0、1、2の座標は図Tech05-015のとおりになります。
図Tech05-015■前面の頂点番号と座標
|
立方体の各面の頂点には、右上隅(0)から左上隅(1)、左下隅(2)の反時計回りの順に番号をつける。1辺の半分の値を変数nUnitに設定。
|
それでは、Sprite3Dクラスを定義します。立方体の面をつくるクラスで、タイムラインが要らないため、MovieClipクラスのスーパークラスであるSpriteを継承することにします(Word Tech05-001)。画像は[ライブラリ]にビットマップを読込んでおき、Sprite3Dインスタンスに動的に配置します。
|
Word Tech05-001■Spriteクラス
Spriteは、MovieClipクラスのスーパークラスで、MovieClipからタイムラインの機能を省いたものです。インスタンスの内部にグラフィックを描けますし、DisplayObjectContainerクラスを継承しますので表示リストに子インスタンスをもつこともできます。
インスタンスを動的に生成するなど、タイムラインを必要としないビジュアルエレメントには、Spriteインスタンスが適しています。また、そのようなカスタムクラスを定義するときは、Spriteクラスを継承するとよいでしょう。
|
Sprite3Dクラス(スクリプトTech05-004)には、面の3つの頂点番号(図Tech05-015では、0、1、2)を格納するために、配列のプロパティがひとつ宣言されます。このプロパティのアクセス制御の属性はprivateとし、get/setアクセサメソッド(08-04「get/setアクセサメソッド」参照)により値を取得・設定します。
メソッドは前掲フレームアクション(スクリプトTech05-002)の関数xTransformMovieClipPoints()を、インスタンス自身がターゲットとなるように書替え、メソッド名もtransformSpritePoints()としました。具体的には、もとの関数の引数からターゲットの指定(第1引数)を外し、メソッド本体でアクセスするプロパティやメソッドの参照(ターゲット)はインスタンス自身としています。
スクリプトTech05-004■立方体の面をつくるSprite3Dクラスの定義
|
package {
import flash.display.Sprite;
import flash.geom.Matrix;
import flash.geom.Point;
public class Sprite3D extends Sprite {
private var _vertex:Array;
public function Sprite3D() {
}
public function get vertex():Array {
return _vertex;
}
public function set vertex(vertex_array:Array):void {
_vertex = vertex_array;
}
public function transformSpritePoints(point0:Point, point1:Point, point2:Point):void {
transform.matrix = new Matrix();
var nWidth:Number = width;
var nHeight:Number = height;
transform.matrix = MathUtils.transformPoints(nWidth, nHeight, point0, point1, point2);
}
}
}
|
つぎに、3次元座標を管理するPoint3Dクラスの定義です。3次元空間における(x, y, z)座標をプロパティとしてもつとともに、座標を回転するメソッドも定義します。3次元座標の観点と聞くと、難しそうに思えるかもしれません。しかし、実はその基本はすでにご紹介しています。それは、Matrix.rotate()メソッドです(表Tech05-002「変換行列のプロパティ値とその適用結果」参照)。xy平面における原点(0, 0)を中心とした回転というのは、3次元空間で考えればz軸を中心とした回転です(図Tech05-016)。3次元空間の回転を行うには、あとx軸とy軸の回転を加えればよいのです。
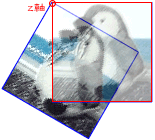
図Tech05-016■xy平面の回転は3次元ではz軸が中心
|
zy平面の原点(0, 0)は、3次元空間ではz軸になる。
|
普通の地球儀は、南北を軸として東西方向に回転します。けれど、ちょっと高級な地球儀には、もうひとつ回転軸を加えて南北にも自由に回せるものがあります。それと同じで、3次元の座標は、yz平面をx軸で回し、zx平面をy軸で回し、さらにxy平面をz軸で回せば、原点(0, 0, 0)を中心とした回転が表せるのです。
したがって、各平面における回転には、Matrix.rotate()メソッドが使えます。ただし、それぞれの軸で回転した結果の座標は、(z軸の場合意外は)(x, y)でなく各平面に対応した軸で読替える必要があります。座標の変換には、引数で渡すPointインスタンスの座標を回転して、その結果をPointインスタンスで返すメソッドMatrix.transformPoint()が利用できます(Word Tech05-002)。
|
Word Tech05-002■Matrix.transformPoint()メソッド
つぎのシンタックスで、Pointインスタンスに変換行列を適用します。
Matrixインスタンス.transformPoint(Pointインスタンス:Point):Point
Matrixインスタンスの変換行列をPointインスタンスの(x, y)座標に対して適用し、座標の変換されたPointインスタンスを返します。
Pointインスタンス ー 変換行列を適用したいPointインスタンスです。この引数のPointインスタンスそのものは値は変わりません。
なお、[ヘルプ]における本メソッドの項は、引数を「行列変換の結果として得られるポイント」と説明しています。しかし、英語原文は、"The point for which you want to get the result of the Matrix transformation"となっており、「Matrixの変換を適用した結果がほしいポイント」と訳すべきでしょう。
|
Point3Dクラスの定義は、以下のスクリプトTech05-005のとおりです。3次元座標の(x, y, z)は、get/setアクセサメソッドとして定義します。回転のメソッドrotate()は、xyz各軸がそれぞれ中心となる3つの回転角のラジアン値を引数として受取り、インスタンスの(x, y, z)座標値に回転の変換を与えます。
rotate()メソッド本体では、各軸ごと(たとえばx軸用)に新規のMatrixインスタンスを作成したうえで(x軸であれば引数nRadianXのラジアン値で)回転し、各平面(x軸ならyz平面)上の回転前の座標をもったPointインスタンスから、Matrix.transformPoint()メソッドにより回転後のPointインスタンスを得ます。そして、そのようにして取得した回転後の各座標値を、Point3Dインスタンスの新たな(x, y, z)座標に設定しています。
スクリプトTech05-005■3次元座標を管理するPoint3Dクラスの定義
|
// ActionScript 3.0クラス定義ファイル: Point3D.as
package {
import flash.geom.Matrix;
import flash.geom.Point;
public class Point3D {
private var _x:Number;
private var _y:Number;
private var _z:Number;
public function Point3D(nX:Number, nY:Number, nZ:Number) {
x = nX;
y = nY;
z = nZ;
}
public function get x():Number {
return _x;
}
public function set x(nX:Number) {
_x = nX;
}
public function get y():Number {
return _y;
}
public function set y(nY:Number) {
_y = nY;
}
public function get z():Number {
return _z;
}
public function set z(nZ:Number) {
_z = nZ;
}
public function rotate(nRadianX:Number,nRadianY:Number,nRadianZ:Number):void {
var nX:Number = x;
var nY:Number = y;
var nZ:Number = z;
// X軸で回転
var matrixX:Matrix = new Matrix();
matrixX.rotate(nRadianX);
var pointX:Point = matrixX.transformPoint(new Point(nY, nZ));
nY = pointX.x;
nZ = pointX.y;
// Y軸で回転
var matrixY:Matrix = new Matrix();
matrixY.rotate(nRadianY);
var pointY:Point = matrixY.transformPoint(new Point(nZ, nX));
nZ = pointY.x;
nX = pointY.y;
// Z軸で回転
var matrixZ:Matrix = new Matrix();
matrixZ.rotate(nRadianZ);
var pointZ:Point = matrixZ.transformPoint(new Point(nX, nY));
nX = pointZ.x;
nY = pointZ.y;
x = nX;
y = nY;
z = nZ;
}
}
}
|
1面のみのサンプルで最後に作成するのは、面の画像を[ライブラリ]に格納したFlashムービー(FLA)ファイルに記述するフレームアクションです。立方体の頂点を管理し、その座標に回転を加えたうえで、それらの頂点に合わせて面を配置します。そのおもな関数と処理の流れを、先にざっと確認します。
第1に、初期設定として、関数setCubeData()が立方体の頂点番号と、それぞれの座標値を配列に納めます。第2に、関数initializeCube()は、面のSprite3Dインスタンスを生成して、対応する頂点番号を設定し、[ライブラリ]からビットマップ画像を加えます。第3のdrawCube()メソッドは、各頂点座標をマウスポインタの位置に対応して回転したうえで、Sprite3Dインスタンスを対応する頂点に合わせて変形します。そして、各頂点座標を回転させる関数が第4のtransformCubePoints()です。
スクリプトTech05-006■立方体の頂点と面をコントロールするフレームアクション
|
// タイムライン: メイン
// 第1フレームアクション
var myPosition:Point = new Point(stage.stageWidth/2, stage.stageHeight/2);
var oRotations:Object = {x:0, y:0, z:0};
var nUnit:Number = 100/2;
var cubePoints_array:Array = new Array();
var holderSprite:Sprite = new Sprite();
var nSensitivity:Number = 1/500;
var mySprite:Sprite3D;
holderSprite.x = myPosition.x;
holderSprite.y = myPosition.y;
addChild(holderSprite);
setCubeData();
initializeCube();
drawCube();
holderSprite.addEventListener(Event.ENTER_FRAME, drawCube);
function setCubeData():void {
cubePoints_array[0] = new Point3D(nUnit, -nUnit, -nUnit);
cubePoints_array[1] = new Point3D(-nUnit, -nUnit, -nUnit);
cubePoints_array[2] = new Point3D(-nUnit, nUnit, -nUnit);
}
function initializeCube():void {
mySprite = new Sprite3D();
holderSprite.addChild(mySprite);
mySprite.vertex = [0, 1, 2];
mySprite.addChild(new Bitmap(new Image(0, 0)));
}
function drawCube(eventObject:Event=null):void {
// oRotations.x = -holderSprite.mouseY*nSensitivity; // 動作確認後に有効にする
oRotations.y = holderSprite.mouseX*nSensitivity;
var points2d:Array = transformCubePoints(cubePoints_array, oRotations);
var n0:Number = mySprite.vertex[0];
var n1:Number = mySprite.vertex[1];
var n2:Number = mySprite.vertex[2];
mySprite.transformSpritePoints(points2d[n0], points2d[n1], points2d[n2]);
}
function transformCubePoints(points_array:Array, oMyRotations:Object):Array {
var points2D_array:Array=new Array();
var nRadianX:Number = oMyRotations.x;
var nRadianY:Number = oMyRotations.y;
var nRadianZ:Number = oMyRotations.z;
var nLength:Number = points_array.length;
for (var i:Number=0; i<nLength; ++i) {
var myPoint3D:Point3D = points_array[i];
myPoint3D.rotate(nRadianX, nRadianY, nRadianZ);
points2D_array[i] = new Point(myPoint3D.x, myPoint3D.y);
}
return points2D_array;
}
|
それでは、関数本体の処理も含めて、もう少し細かく説明します。タイムラインの変数宣言のうち、holderSpriteは空のSpriteインスタンスで、のちにinitializeCube()関数により立方体の面を構成するSprite3Dインスタンスが子として加えられます。今のところは1面のみ納め、あとで完全な立方体のサンプルを作成するときに6面が格納されます。変数myPositionは、インスタンスholderSpriteの位置をPointインスタンスで保持します。
関数setCubeData()は、立方体の各頂点座標をタイムライン変数の配列cubePoints_arrayに格納します。インデックスは頂点番号とし、エレメントとなる座標はPoint3Dインスタンスで加えます。まだ1面のみですので、頂点番号と座標値は前掲図Tech05-015に示した3点の値のみを用います(変数nUnitは1辺の1/2の値)。完全な立方体のサンプルでは、頂点番号0から5までの6頂点が設定されます(前掲図Tech05-014左図)。
図Tech05-015■前面の頂点番号と座標(再掲)

関数initializeCube()では、まずタイムライン変数mySpriteに面のSprite3Dインスタンスを代入しています。完全な立方体では6面が必要になりますので、その際は配列を変数とし、そこに6つのSprite3Dインスタンスを納めるように修正します。つぎに、Sprite3Dインスタンスには、その面が対応する3つの頂点番号を配列でSprite3D.vertexプロパティに設定します。そして、[ライブラリ]のビットマップからBitmapインスタンスを作成して、Sprite3Dインスタンスの子として加えます。なお、ビットマップには、Imageというクラス名を設定しておきます。
関数drawCube()は、SpriteインスタンスholderSpriteのDisplayObject.enterFrameイベントにリスナー関数として登録され、マウスポインタの位置に対応して立方体を回転させます。まず、Objectインスタンスを納めるタイムライン変数oRotationsには、x軸y軸z軸それぞれを中心として回転させるパラメータの値(ラジアン値)を設定します。マウスポインタを垂直に動かしたときがx軸、水平に動かしたときはy軸を中心として、立方体が回転するものとします(変数nSensitivityは調整値)。なお、動作が確かめやすいように、初めはx軸中心に回転させるステートメントはコメントアウトしておきます。
つぎに、drawCube()関数本体から、立方体の座標cubePoints_arrayと回転させるパラメータoRotationsを引数として、関数transformCubePoints()を呼出しています。この関数は、回転させた立方体の各頂点の(x, y)座標を配列で返します。配列には、頂点番号のインデックスに、その頂点座標のPointインスタンスがエレメントとして納められています。そこで、面のSprite3Dインスタンスから3つの頂点番号を取出せば、それら頂点の回転後の座標をPointインスタンスとして得ることができます。
drawCube()関数本体の最後のステートメントは、その回転後の3頂点のPointインスタンスを引数として、Sprite3D.transformSpritePoints()メソッドを呼出し、座標値に合わせてインスタンスを変換しています。
関数transformCubePoints()は、立方体の6頂点の座標をもった配列(cubePoints_array)とx軸y軸z軸の各回転角の値をもったObjectインスタンス(oMyRotations)が引数となり、回転後の各頂点の(x, y)座標がPointインスタンスとしてエレメントに納められた配列を返します。関数本体の処理は、まず第2引数のObjectインスタンスから、x軸y軸z軸それぞれに対する回転角の数値を取出します。そして、第1引数の配列から頂点座標のPoint3Dインスタンスをforループで順に取出し、各Point3Dインスタンスの(x, y)座標値をPointインスタンスとして配列に納めたうえで、その配列を返します。
上記フレームアクション(スクリプトTech05-006)では、関数drawCube()本体のx軸で回転する最初のステートメントがコメントアウトされていますので、[ムービープレビュー]を見るとマウスポインタの水平方向の動きのみに反応して、面のSprite3Dインスタンスはy軸を中心とした水平方向にだけ回転します。その正しい動作が確かめられたら、コメントアウトを外してx軸y軸の両方で面のインスタンスを回転してみましょう(図Tech05-017)。
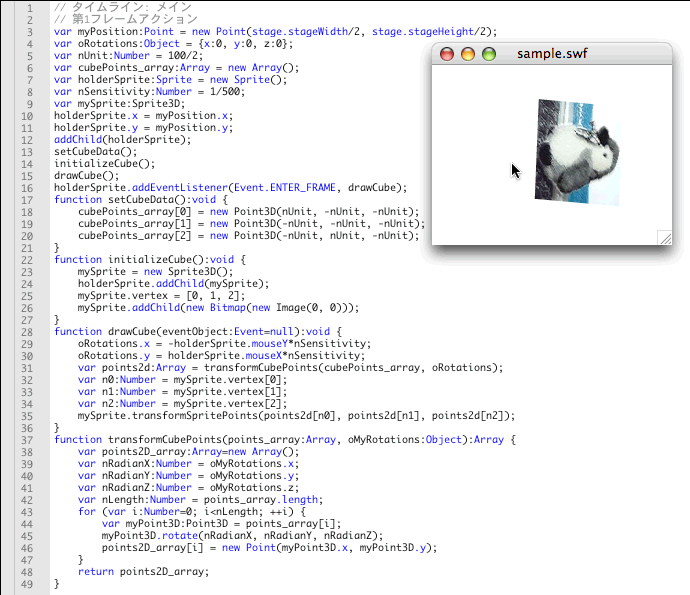
図Tech05-017■マウスポインタの動く方向に対応して面のインスタンスがx軸とy軸を中心に回転する
|
マウスポインタを水平に動かすとy軸、垂直に動かせばx軸を中心として、面のSprite3Dインスタンスが回転する。
|
|
Tips Tech05-008■z軸を中心とした回転
今回のサンプルでは、x軸y軸z軸の各回転角の値をもったObjectインスタンスoMyRotationsのzプロパティの値はつねに0です。つまり、z軸で回転させることはありません。これは、マウスポインタの動きが水平と垂直の2軸しかないため、z軸で回す操作が加えにくいからです。しかし、スクリプトの処理はz軸の扱いを含めていますので、必要があればいつでも追加できます。
|
|
Tips Tech05-009■頂点の(x, y)座標だけで面を変換する理由
関数transformCubePoints()は、立方体の頂点座標を回転したうえで、それらの(x, y)座標がPointインスタンスとしてエレメントに納められた配列を返します。そして、返された配列の(x, y)座標により関数drawCube()が立方体の各面を変換しています。したがって、立方体の頂点のz座標は、面の変換には用いられていません。
これは前述(Tips Tech05-001「アフィン変換」参照)のとおり、変換行列ではパースがかけられないため、z座標は画面への投影に影響を与えないからです。つまり、このサンプルにおける3D表現には、遠近感がないことを意味します。
|
●6面の立方体を3次元で回転させる
今つくったサンプルを6面の完全な立方体の回転にするには、前掲フレームアクション(スクリプトTech05-006)に大きく手を入れます。その際、このスクリプトもクラスとして定義し直すことにしましょう。
[ライブラリ]のシンボルには、[シンボルプロパティ]のダイアログボックスで[クラス]が設定できました。[プロパティ]インスペクタでドキュメントのプロパティとして[ドキュメントクラス]にクラスを入力すれば、メインタイムラインにクラスが設定されます(図Tech05-018)。そうすると、Flashムービー(FLA)ファイル内には、一切スクリプトを記述せずに済みます。
図Tech05-018■プロパティインスペクタの[ドキュメントクラス]にクラスを設定

|
[ドキュメントクラス]は、メインタイムラインに設定される。
|
ドキュメントクラスの定義の仕方は、基本的にMovieClipシンボルに設定するクラスと同じです。つまり、クラスにはアクセス制御の属性としてpublicを指定し、またMovieClipクラスを継承する必要があります。クラス名はもちろん任意です。今回はMainとします。
package {
import flash.display.MovieClip;
public class Main extends MovieClip {
}
}
|
Tips Tech05-010■[ドキュメントクラス]の継承するクラス
[ドキュメントクラス]に設定するクラスは、Spriteクラスを継承しても動作はします。しかしそうすると、複数フレームは使えず、フレームにスクリプトが一切書けません(コメントも不可です)。したがって、通常はMovieClipクラスを継承すべきでしょう。
|
面となる長方形(正方形)は、3つの角の座標が決まれば平行四辺形への変換は定まりました。したがって、立方体も8つの頂点すべての座標を管理する必要はなく、最小限6頂点の座標を決めれば6面の変換と配置は可能です(図Tech05-019左図)。立方体の中心に原点(0, 0, 0)を置き、1辺の長さはnUnit*2として、6頂点の座標は図Tech05-019右図のように定めます。6面はそれぞれ3つの頂点番号をもちます。
図Tech05-019■立方体の頂点番号と座標を決める
|
立方体の少なくとも6頂点の座標により、各面の配置が定まる。立方体の中心を原点(0, 0)、1辺の長さをnUnit*2とする。
|
それでは、前掲フレームアクション(スクリプトTech05-006)をクラスMainとして定義し直す際のポイントについて、関数(メソッド)を中心に概観しておきましょう。まず、メソッドsetCubeData()では、頂点番号が6つに増えます。面の数も6つ必要になりますので、プロパティとして新たに配列(faces_array)を宣言し、各面がもつ3つの頂点番号を配列で納めます(各面のもつ3つの頂点番号については、前掲図Tech05-019左図参照)。なお、3つの頂点番号は、反時計回り(前面であれば、0、1、2)の順に指定することとします。
private var nUnit:Number = 100/2;
private var cubePoints_array:Array = new Array();
private var faces_array:Array = new Array();
private function setCubeData():void {
cubePoints_array[0] = new Point3D(-nUnit, -nUnit, -nUnit);
cubePoints_array[1] = new Point3D(-nUnit, nUnit, -nUnit);
cubePoints_array[2] = new Point3D(nUnit, nUnit, -nUnit);
cubePoints_array[3] = new Point3D(-nUnit, -nUnit, nUnit);
cubePoints_array[4] = new Point3D(nUnit, -nUnit, nUnit);
cubePoints_array[5] = new Point3D(nUnit, nUnit, nUnit);
// 各面のもつ3つの頂点番号
faces_array.push([0, 1, 2]); // 前面
faces_array.push([3, 4, 5]); // 後面
faces_array.push([4, 3, 0]); // 上面
faces_array.push([5, 2, 1]); // 底面
faces_array.push([1, 0, 3]); // 左側面
faces_array.push([2, 5, 4]); // 右側面
}
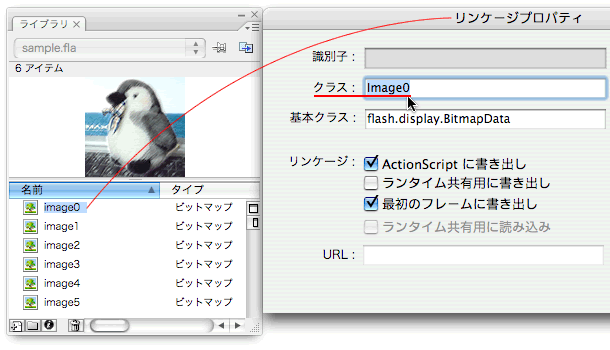
つぎに、initializeCube()メソッドにはforループの処理を加えて、6面分のSprite3Dインスタンスを生成し、それぞれに別のビットマップ画像を設定します。6つのビットマップ画像にはImage0からImage5までのクラス名を設定したうえで(図Tech05-020)、プロパティ宣言した配列(images_array)に格納しておきます。
図Tech05-020■6つのビットマップ画像にクラスを設定
|
クラス名は、Image0からImage5まで(シンボルと同じ連番)とする。
|
注意する点は、インスタンスプロパティfaces_arrayから頂点番号の配列を取出し、面のSprite3Dインスタンスのvertexプロパティに設定したあと、そのSprite3Dインスタンスを配列エレメントとして差替えてしまっていることです。なお、クラスの参照を入れる変数(imageClass)には、Class型を指定します。
private var images_array:Array = [Image0, Image1, Image2, Image3, Image4, Image5];
private var holderSprite:Sprite = new Sprite();
private function initializeCube():void {
var nLength:Number = faces_array.length;
for (var i:Number=0; i<nLength; ++i) {
var imageClass:Class = images_array[i];
var mySprite:Sprite3D = new Sprite3D();
holderSprite.addChild(mySprite);
mySprite.vertex = faces_array[i]; // 頂点番号の配列をSprite3D.vertexプロパティに設定
faces_array[i] = mySprite; // 配列エレメントをSprite3Dインスタンスで差替え
mySprite.addChild(new Bitmap(new imageClass(0, 0)));
}
}
そして、メソッドdrawCube()は、変換するSprite3Dインスタンスが6面に増えたため、forループによる処理が加わることになります。最後のtransformCubePoints()メソッドは、クラスに定義するためアクセス制御の属性privateが指定されるほかは、もとのフレームアクションと実質的な処理は変わりません。また、コンストラクタも、基本的にフレームアクションのステートメントが、メソッド本体に加えられるだけです。
private function drawCube(eventObject:Event=null):void {
oRotations.x = -holderSprite.mouseY*nSensitivity;
oRotations.y = holderSprite.mouseX*nSensitivity;
var points2d:Array = transformCubePoints(cubePoints_array, oRotations);
var nLength:Number=faces_array.length;
for (var i:Number=0; i < nLength; ++i) {
var mySprite:Sprite3D = faces_array[i];
var n0:Number = mySprite.vertex[0];
var n1:Number = mySprite.vertex[1];
var n2:Number = mySprite.vertex[2];
mySprite.transformSpritePoints(points2d[n0], points2d[n1], points2d[n2]);
}
}
以上の追加や修正を行って定義し直したドキュメントクラスMainは、つぎのスクリプトTech05-007のとおりです。
スクリプトTech05-007■立方体の頂点と面をコントロールするドキュメントクラスMain
|
// ActionScript 3.0クラス定義ファイル: Main.as
package {
import flash.display.Sprite;
import flash.display.MovieClip;
import flash.display.Bitmap;
import flash.geom.Point;
import flash.events.Event;
public class Main extends MovieClip {
private var myPosition:Point=new Point(stage.stageWidth/2, stage.stageHeight/2);
private var oRotations:Object = {x:0,y:0,z:0};
private var images_array:Array = [Image0, Image1, Image2, Image3, Image4, Image5];
private var nUnit:Number = 100/2;
private var cubePoints_array:Array=new Array();
private var holderSprite:Sprite = new Sprite();
private var nSensitivity:Number = 1/500;
private var faces_array:Array = new Array();
public function Main() {
setCubeData();
addChild(holderSprite);
holderSprite.x = myPosition.x;
holderSprite.y = myPosition.y;
initializeCube();
drawCube();
holderSprite.addEventListener(Event.ENTER_FRAME, drawCube);
}
private function setCubeData():void {
cubePoints_array[0] = new Point3D(-nUnit, -nUnit, -nUnit);
cubePoints_array[1] = new Point3D(-nUnit, nUnit, -nUnit);
cubePoints_array[2] = new Point3D(nUnit, nUnit, -nUnit);
cubePoints_array[3] = new Point3D(-nUnit, -nUnit, nUnit);
cubePoints_array[4] = new Point3D(nUnit, -nUnit, nUnit);
cubePoints_array[5] = new Point3D(nUnit, nUnit, nUnit);
faces_array.push([0, 1, 2]); // 前面
faces_array.push([3, 4, 5]); // 後面
faces_array.push([4, 3, 0]); // 上面
faces_array.push([5, 2, 1]); // 底面
faces_array.push([1, 0, 3]); // 左側面
faces_array.push([2, 5, 4]); // 右側面
}
private function initializeCube():void {
var nLength:Number = faces_array.length;
for (var i:Number=0; i<nLength; ++i) {
var imageClass:Class = images_array[i];
var mySprite:Sprite3D = new Sprite3D();
holderSprite.addChild(mySprite);
mySprite.vertex = faces_array[i];
faces_array[i] = mySprite;
mySprite.addChild(new Bitmap(new imageClass(0, 0)));
}
}
private function drawCube(eventObject:Event=null):void {
oRotations.x = -holderSprite.mouseY*nSensitivity;
oRotations.y = holderSprite.mouseX*nSensitivity;
var points2d:Array = transformCubePoints(cubePoints_array, oRotations);
var nLength:Number=faces_array.length;
for (var i:Number=0; i < nLength; ++i) {
var mySprite:Sprite3D = faces_array[i];
var n0:Number = mySprite.vertex[0];
var n1:Number = mySprite.vertex[1];
var n2:Number = mySprite.vertex[2];
mySprite.transformSpritePoints(points2d[n0], points2d[n1], points2d[n2]);
}
}
private function transformCubePoints(points_array:Array, oMyRotations:Object):Array {
var points2D_array:Array = new Array();
var nRadianX:Number = oMyRotations.x;
var nRadianY:Number = oMyRotations.y;
var nRadianZ:Number = oMyRotations.z;
var nLength:Number = points_array.length;
for (var i:Number=0; i < nLength; ++i) {
var myPoint3D:Point3D = points_array[i];
myPoint3D.rotate(nRadianX, nRadianY, nRadianZ);
points2D_array[i] = new Point(myPoint3D.x, myPoint3D.y);
}
return points2D_array;
}
}
}
|
Mainクラスの定義で、回転する立方体のアニメーションはほぼ9割方できあがりました。しかし、[ムービープレビュー]で動きを確かめると、明らかにおかしな表示になります。これは、面の重ね順の管理をしていないためです。つまり、手前に表示されるべき面が、後ろに位置する面の裏側に隠れてしまうことがあるのです(図Tech05-021)。
図Tech05-021■立方体の6面の重ね順が管理されていない

|
手前に表示されるべき面が、後ろに位置する面の裏側に隠れている。
|
面の重なりは、Sprite3Dクラスで対応することにします。というのは、重なりの順番まで管理する必要はないからです。立方体の6面のうち、見えるのは手前側の3面までです。奥の側の裏返った3面は表示しなくてよいのです。各面には3つの頂点番号を、反時計回りに設定しました。面が裏返ると、3頂点の位置は反時計回りでなくなります。したがって、各面のSprite3Dインスタンスは、自らの頂点番号の座標が反時計回りでなかったら、表示しないという仕組みにすればよいのです。
[*イラスト候補●Tech05-003] 3つの頂点の位置が反時計回りなら表向き、そうでなければ裏向き。
参考画像

|
クラスSprite3Dには、新たにメソッドisFront()を定義します。このメソッドは、Sprite3Dインスタンスが表向きか裏向きかを、Boolean(論理)値のtureまたはfalseで返します。そのうえで、transformSpritePoints()メソッドには、以下のような条件判定を加えます。つまり、Sprite3Dインスタンスが表向きなら変換して表示し、裏向きの場合には非表示にして変換の処理もしないということです。なお、if条件は代入式ですので、isFront()メソッドの戻り値がDisplayObject.visibleプロパティに設定されるとともに、その値によってifステートメントが処理されます(Tips 08-010「if条件に指定した代入式」参照)。
internal function transformSpritePoints(point0:Point, point1:Point, point2:Point):void {
// 面が裏向きなら非表示/表向きであれば変換
if (visible = isFront(point0, point1, point2)) {
transform.matrix = new Matrix();
var nWidth:Number = width;
var nHeight:Number = height;
transform.matrix = MathUtils.transformPoints(nWidth, nHeight, point0, point1, point2);
}
}
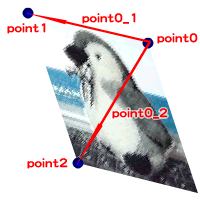
メソッドisFront()は、引数として渡された3つの頂点番号の順に座標を評価して、それらの位置が反時計回りならtrueを、そうでなければfalseを返します。その判定は、Point.subtract()メソッド()を用いて、最初の頂点(point0)から見た他のふたつの頂点(point1とpoint2)の座標を求め(point0_1とpoint0_2)、それらの(x, y)座標値を比べることにより行っています(図Tech05-022)。
図Tech05-022■3つの頂点の位置が反時計回りかどうかを判定する
|
最初の頂点(point0)から見た他のふたつの頂点(point1とpoint2)の座標を求め(point0_1とpoint0_2)、それらの(x, y)座標値を比べて判別する。
|
ふたつの座標の位置による判定は、それぞれのxyの各座標値を正負で場合分けすれば、面倒ではあるものの、さほど難しい評価ではありません。ただ、本サンプルのisFront()メソッド(スクリプトTech05-008)は、複数の場合をパズル的に組合わせて、ステートメント数を減らしています。とはいえ、判別に使っているのは四則演算とその結果の大小比較だけです。本章ではこの処理内容はテーマから外れますので、解説は割愛します。興味のある読者は、3つの頂点の位置を図に描いて、その判定の結果を確かめてみてください。
スクリプトTech05-008■面の表示/非表示の制御を加えたSprite3Dクラス
|
// ActionScript 3.0クラス定義ファイル: Sprite3D.as
package {
import flash.display.Sprite;
import flash.geom.Matrix;
import flash.geom.Point;
public class Sprite3D extends Sprite {
private var _vertex:Array;
public function Sprite3D() {
}
public function get vertex():Array {
return _vertex;
}
public function set vertex(vertex_array:Array):void {
_vertex=vertex_array;
}
internal function transformSpritePoints(point0:Point, point1:Point, point2:Point):void {
// 面が裏向きなら非表示/表向きであれば変換
if (visible = isFront(point0, point1, point2)) {
transform.matrix = new Matrix();
var nWidth:Number = width;
var nHeight:Number = height;
transform.matrix = MathUtils.transformPoints(nWidth, nHeight, point0, point1, point2);
}
}
internal function isFront(point0:Point, point1:Point, point2:Point):Boolean {
var bResult:Boolean;
var point0_1:Point = point1.subtract(point0);
var point0_2:Point = point2.subtract(point0);
var nX0_1:Number = point0_1.x;
var nY0_1:Number = point0_1.y;
var nX0_2:Number = point0_2.x;
if (!nX0_1) {
bResult = (nY0_1>0) == (nX0_2>0);
} else {
var nY0_2:Number = point0_2.y;
if (!nX0_2) {
bResult = (nY0_2>0) != (nX0_1>0);
trace(bResult);
} else {
bResult = (nY0_1/nX0_1<nY0_2/nX0_2) == ((0<nX0_1) == (0>nX0_2));
}
}
return bResult;
}
}
}
|
修正結果を[ムービープレビュー]で確かめると、今度は面の表示/非表示が正しくコントロールされて、立方体の回転が表現されます(図Tech05-023)。
図Tech05-023■Sprite3Dクラスにより面の表示/非表示がコントロールされる

|
Sprite3Dクラスは、裏向きの面を非表示にし、表向きの面だけを変換して表示する。
|
|
Maniac! Tech05-002■裏面を非表示にする
3次元空間の処理は、CPUの負荷も高まりやすくなります。したがって、立方体の裏返しの面のように表示する必要のないインスタンスの処理は、できるだけ省く方が効率は上がります。
|
[Prev/Next]
作成者: 野中文雄
作成日: 2008年8月11日


















