コンピュータグラフィックス(CG)では座標空間におけるオブジェクトの移動や拡大・縮小、あるいは回転などの変換を数学の行列で処理することがよくあります。そうすると、位置(DisplayObject.x/DisplayObject.y)やスケール(DisplayObject.scaleX/DisplayObject.scaleY)、または角度(DisplayObject.rotation)といったプロパティをひとつひとつ操作するよりも、それらを組合わせた変換が決まった演算の手順で行えるため、複雑な処理にも応用しやすいからです。
ActionScript 3.0ではそのような行列による変換を行う場合、2次元平面にはMatrixクラス、3次元空間はMatrix3Dクラスを用います。前者のMatrixクラスは、Flash Player 9から備わっています。3次元空間の扱いを学ぶ前に、ひとつ次元の少ない2次元平面で、行列を使った処理の基本的な考え方を理解しておきましょう。
○03-01 Matrixクラスのメソッドを使った座標変換
「Matrix」というのは、英語で数学の「行列」を意味します(あの映画のことではありません)。行列はコンピュータグラフィックスの内部的には、フィルタなどさまざまな画像処理に用いられています。しかし、ActionScript 3.0のMatrixクラスは、座標空間でインスタンスを変換する行列です。このような行列を「変換行列」(transformation matrix)と呼びます。
DisplayObjectインスタンスを2次元平面で変換するMatrixオブジェクトは、DisplayObject.transformプロパティ(シンタックス02-001「消失点を操作するためのプロパティ」参照)からTransform.matrixプロパティを参照して取得します。すると、Matrixクラスのメソッドにより、DisplayObjectインスタンスのxy座標を回転したり、拡大・縮小したり、あるいは平行移動することができます(シンタックス03-001)。
シンタックス03-001■Matrixオブジェクトにより回転・伸縮・平行移動するためのプロパティとメソッド
|
Transform.matrixプロパティ
|
|
文法
|
matrix:Matrix
|
|
プロパティ値
|
DisplayObjectインスタンスに適用されるMatrixオブジェクトの参照。インスタンスの2次元平面における平行移動や伸縮、回転、傾斜などの座標変換を表す。
|
|
Matrix.translate()メソッド
|
|
文法
|
translate(tx:Number, ty:Number):void
|
|
概要
|
インスタンスに適用される平行移動の水平および垂直ピクセル数を設定する。
|
|
引数
|
tx:Number ― 移動する水平ピクセル数。
ty:Number ― 移動する垂直ピクセル数。
|
|
戻り値
|
なし。
|
|
Matrix.scale()メソッド
|
|
文法
|
scale(a:Number, d:Number):void
|
|
概要
|
インスタンスに適用される拡大・縮小の水平および垂直比率を設定する。
|
|
引数
|
a:Number ― 拡大・縮小する水平方向の比率。
d:Number ― 拡大・縮小する垂直方向の比率。
|
|
戻り値
|
なし。
|
|
Matrix.rotate()メソッド
|
|
文法
|
rotate(angle:Number):void
|
|
概要
|
インスタンスに適用される回転の角度をラジアンで設定する。
|
|
引数
|
angle:Number ― 回転するラジアンの角度。
|
|
戻り値
|
なし。
|
DisplayObjectインスタンスからMatrixオブジェクトの参照を得て、Matrixクラスの上記メソッドによりインスタンスの座標を変換する手順はつぎのとおりです。
【Matrixオブジェクトを使ったDisplayObjectインスタンスの変換の手順】
- DisplayObject.transformプロパティのTransform.matrixプロパティからMatrixインスタンスを取得する。
- MatrixクラスのメソッドによりMatrixインスタンスを変換する。
- 変換の処理が加えられたMatrixインスタンスをDisplayObject.transformプロパティのTransform.matrixプロパティに設定する。
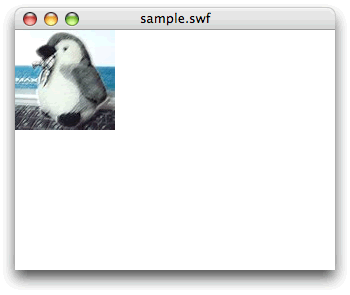
たとえば、メインタイムラインの基準点に配置されたMovieClipインスタンスmy_mcに対し、(1)水平方向に1.5倍、垂直方向に1.2倍拡大し、(2)時計回りに30度(= π/6ラジアン)回転して、(3)x座標を80ピクセル、y座標を40ピクセル移動するには、つぎのようなフレームアクションを記述します。なお、MovieClipインスタンスの基準点は左上隅だとします(図03-001)。
スクリプト03-001■Matrixオブジェクトによりインスタンスに拡大・回転・移動の変換を適用
// フレームアクション
// タイムラインにMovieClipインスタンスmy_mcを配置
- var myMatrix:Matrix = my_mc.transform.matrix;
- myMatrix.scale(1.5, 1.2);
- myMatrix.rotate(Math.PI/6);
- myMatrix.translate(80, 40);
- my_mc.transform.matrix = myMatrix;
|
図03-001■Matrixオブジェクトで拡大・回転・移動の変換を適用されたインスタンス
 |
→ |
 |
|
座標変換の原点は、インスタンスの配置された親インスタンス(タイムライン)の基準点に固定される。
|
スクリプト03-001の処理は、前記「Matrixオブジェクトを使ったDisplayObjectインスタンスの変換の手順」にしたがっています。
[1]まず、スクリプト第1行目が手順1です。MovieClipインスタンス(my_mc)のDisplayObject.transformプロパティのTransform.matrixプロパティから、Matrixインスタンスを取出して変数(myMatrix)に設定しています。
[2]つぎに、スクリプト第2〜4行目は手順2で、Matrixオブジェクトのメソッドによる変換です。変数のMatrixインスタンスに対して、MovieClipインスタンスに適用する拡大(Matrix.scale())と回転(Matrix.rotate())、および移動(Matrix.translate())の変換をそれぞれ加えています。
[3]そして、スクリプト第5行目が手順3のインスタンスへの変換の適用です。変換後のMatrixオブジェクトを、MovieClipインスタンスのDisplayObject.transformプロパティのTransform.matrixプロパティに設定しています。
スクリプト03-001の処理とその結果について、注意しておきたいことがふたつあります。
第1は、Matrixオブジェクトを適用するためには、前述手順3のとおりDisplayObject.transformプロパティのTransform.matrixプロパティに、必ず変換後のMatrixインスタンスを代入しなければならないということです。手順1でTransform.matrixプロパティから取得したMatrixオブジェクトを手順2により操作しただけでは、DisplayObjectインスタンスに変換は適用されません。
第2に、Matrixオブジェクトの行列による変換は、DisplayObjectインスタンスが配置されている親インスタンス(タイムライン)の座標空間の基準点を原点として行われます。したがって、Matrixクラスの各メソッドにまったく同じ引数を渡したとしても、メソッドを呼出す順序によって変換結果は異なります。
たとえば、上記スクリプト03-001は、インスタンスに図03-002左図のような順序で変換を加えました。そこで、第5行目のMatrix.translate()メソッドを第2行目の上に移動すると、変換結果は図03-002右図のよう変わります。インスタンスが移動しても親インスタンスの座標空間の原点である基準点は動きませんので、つぎにインスタンスを拡大したとき、大きさが変わるだけでなく原点からインスタンスまでの距離も変化します。また、続く回転も原点を中心として行われることになるからです。
- var myMatrix:Matrix = my_mc.transform.matrix;
my_mc.transform.matrix = myMatrix; // ← 第5行目から移動
- myMatrix.scale(1.5, 1.2);
- myMatrix.rotate(Math.PI/6);
- myMatrix.translate(80, 40);
- // my_mc.transform.matrix = myMatrix;
|
図03-002■インスタンスにMatrixクラスの複数のメソッドを変換として適用
|
Matrix.scale()とMatrix.rotate()、Matrix.translate()の各メソッドの適用順序によって、インスタンスの変換結果は異なる。
|
|
Tips 03-001■行列の乗算は順序によって結果が変わる
座標空間の扱いにかぎらず、さまざまな変換の処理で使われる行列の演算には多くの場合乗算が用いられます。行列の乗算は、演算の順序を変えると結果が変わります(交換法則が成立ちません)。したがって、行列の乗算を使った変換の処理は、演算の順序によって結果が異なるのです。
たとえば、画像にモザイクをかけてからぼかすのと、ぼかしてからモザイクをかけたのとでは、(それがどんな画像に加える処理かはさておき)効果が違ってきます(図03-003)。フィルタもその多くが、画像のピクセルに対して行列演算を行っているからです。
図03-003■フィルタの適用の順序による効果の違い

モザイク→ぼかし |

ぼかし→モザイク |
|
画像にモザイクをかけてからぼかすか、ぼかしてからモザイクをかけるか。
|
|
変換の基準点は異なることがあるものの、前述のとおりDisplayObjectクラスのプロパティを使っても、インスタンスを拡大・縮小(DisplayObject.scaleX/DisplayObject.scaleY)したり、回転(DisplayObject.rotation)あるいは移動(DisplayObject.x/DisplayObject.y)することはできます。けれど、これらの変換をDisplayObjectインスタンスとは切離して管理できることが、Matrixクラス(変換行列)を使う利点となります。
たとえば、ひとつのMatrixオブジェクトを複数のインスタンスのDisplayObject.transformプロパティのTransform.matrixプロパティに代入すれば、それらのインスタンスに同じ変換を簡単に設定できます。逆に、Matrixオブジェクトをいくつか用意しておいて、DisplayObjectインスタンスに適用すれば、その変換が簡単に切替えられます。
|
[イラスト] Matrixオブジェクトを使えば、いろいろな変換がワンタッチ。シンボルのように使い回せる。
|
Matrixクラスは変換が組合わせられることを使うと、変換の原点を親インスタンスの基準点以外にすることもできます。たとえば、タイムラインに置いたインスタンスを、そのインスタンス自身の基準点で回転してみましょう。
とはいえ、回転その他の変換の基準点が親インスタンスであることは変えられません。そうであれば、(1)そのインスタンスを親の基準点に移動させればよいのです。そのうえで、(2)インスタンスに回転の変換を適用します。そして、忘れないように、(3)もといた位置に戻します。この3つの変換の組合わせで、インスタンスを自身の基準点で回転させることができます。
つぎのフレームアクションは、タイムラインに置いたMovieClipインスタンスmy_mcを、インスタンス自身の基準点で45度回転させます(図03-004)。
|
var nX:Number = my_mc.x;
var nY:Number = my_mc.y;
var myMatrix:Matrix = my_mc.transform.matrix;
myMatrix.translate(-nX, -nY);
myMatrix.rotate(45);
myMatrix.translate(nX, nY);
my_mc.transform.matrix = myMatrix;
|
図03-004■インスタンス自身の基準点で回転させる

オーサリング時
|
→ |

[ムービープレビュー] |
|
基準点を親タイムラインと一致するように移動したうえで、回転してもとに戻す。
|
インスタンス(my_mc)の基準点の座標は、予め変数(nXとnY)に取っておきます。そして、インスタンスから参照したMatrixオブジェクトに対して、両座標値がマイナスつまり親タイムラインの基準点に移動させる変換(Matrix.translate()メソッド)を加えます。そのうえで、回転を行い(Matrix.rotate()メソッド)、もとの位置に戻しています(Matrix.translate()メソッド)。
インスタンスの基準点以外を中心に回したい場合も、考え方は基本的に同じです。その中心点が親インスタンスの基準点と一致するように動かして、回転すればよいだけのことだからです。つぎのスクリプト03-002は、自身の基準点が左上隅にあるインスタンスを、その中心を原点として、マウスポインタの方向に回します(図03-005)。
スクリプト03-002■インスタンスを指定の中心点でマウスポインタの方向に回転させる
// フレームアクション
// 指定した中心点で回転させるインスタンスmy_mcを配置
- var centerPoint:Point = new Point(my_mc.width / 2, my_mc.height / 2);
- var translatePoint:Point = centerPoint.add(new Point(my_mc.x, my_mc.y));
- var nDeceleration:Number = 0.2;
- addEventListener(Event.ENTER_FRAME, xRotate);
- function xRotate(eventObject:Event):void {
- var mousePoint:Point = new Point(my_mc.mouseX, my_mc.mouseY);
- var myPoint:Point = mousePoint.subtract(centerPoint);
- var nRadian:Number = Math.atan2(myPoint.y, myPoint.x);
- var myMatrix:Matrix = my_mc.transform.matrix;
- myMatrix.translate(-translatePoint.x, -translatePoint.y);
- myMatrix.rotate(nRadian * nDeceleration);
- myMatrix.translate(translatePoint.x, translatePoint.y);
- my_mc.transform.matrix = myMatrix;
- }
|
図03-005■インスタンスを指定の中心点でマウスポインタの方向に回転させる
|
基準点が左上隅にあるインスタンスを、その中心点でマウスポインタの方向に回転させる(右図)。親インスタンスの基準点から指定の中心点までの座標は、Pointインスタンスでベクトル演算により求めた(左図)。
|
スクリプト03-002でDisplayObject.enterFrameイベント(定数Event.ENTER_FRAME)のリスナー関数xRotate()に加えた第9〜13行目の処理は、基本的に前掲のフレームアクションと同じです。ただし、親インスタンスの基準点から子インスタンスに指定した中心点までの座標は、Pointインスタンスを使って、ベクトル演算で求めています(図03-005左図)。
具体的には、スクリプト第1行目は子インスタンスの基準点から指定の中心点までのベクトルとなるPointインスタンスを変数(centerPoint)に納め、第2行目で親の基準点から子の基準点までのPointインスタンス(ベクトル)にPoint.add()メソッドで加算しています(シンタックス03-002。なお、Tips 03-002参照)。
求められたPointインスタンスは、親の基準点から子の中心点までのベクトルになります。したがって、中心点を親インスタンスの基準点に動かすには、Pointインスタンスのxy座標値をマイナスしてMatrix.translate()メソッドに引数として渡します(スクリプト第10行目)。もとの位置に戻すには、引数をプラスにします(スクリプト第12行目)。
シンタックス03-002■Pointクラスの加減算のメソッド
|
Point.add()メソッド
|
|
文法
|
add(secondPoint:Point):Point
|
|
概要
|
参照するPointインスタンスの座標に、引数のPointインスタンスの座標を加算し、新たなPointインスタンスとして返す。
|
|
引数
|
secondPoint:Point ― 座標を加算するPointインスタンス。
|
|
戻り値
|
参照するPointインスタンスのxy座標値に、引数のPointインスタンスのxy座標値がそれぞれ加えられたxy座標値をもつ新たなPointインスタンス。
|
|
Point.subtract()メソッド
|
|
文法
|
subtract(secondPoint:Point):Point
|
|
概要
|
参照するPointインスタンスの座標から、引数のPointインスタンスの座標を減算し、新たなPointインスタンスとして返す。
|
|
引数
|
secondPoint:Point ― 座標を減算するPointインスタンス。
|
|
戻り値
|
参照するPointインスタンスのxy座標値から、引数のPointインスタンスのxy座標値がそれぞれ差引かれたxy座標値をもつ新たなPointインスタンス。
|
|
Tips 03-002■ベクトルの加減算
ベクトルの加減算は、幾何学的に表現することができます。ベクトルAにベクトルBを足すには、Aの終点にBの始点をつなげます。そして、Aの始点とBの終点を結んだ新たなベクトルが、A + Bになります(図03-006左図。なお、前掲図03-005左図参照)。ベクトルAからベクトルBを引くには、ベクトルBの方向を反転し、その終点をAの始点とつなげます。そして、Bの始点とAの終点を結んだ新たなベクトルが、A - Bになります(図03-006右図)。
図03-006■ベクトルの加減算を幾何学的に表す
|
加算はふたつのベクトルをつなげて、始点と終点を結ぶ。減算は引くベクトルの方向を反転して加算する。
|
|
ひとつ補足します。スクリプト03-002は、インスタンスをマウスポインタの向きに減速しながら回転しています。このイーズアウトの動きをさせるには、インスタンスから見たマウスポインタの角度を得る必要があります(前掲表01-001「イーズアウトの公式」参照)。ただし、指定した中心点で回しますので、マウス座標の角度は、インスタンスの基準点ではなく、中心点から測らなければなりません。
そのため、スクリプト第6行目でインスタンスの基準点から見たマウスポインタの座標のベクトル(mousePoint)を得たうえで、スクリプト第1行目の基準点から指定の中心点までのベクトル(centerPoint)を、スクリプト第7行目でPoint.subtract()メソッドにより引き算して、中心点からマウス座標のベクトル(myPoint)を求めています(図03-007)。
図03-007■中心点からマウス座標までのベクトルを引き算で求める
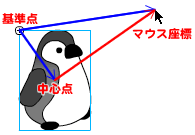
|
基準点から見たマウス座標と中心点座標のベクトルの引き算で、中心点からマウス座標のベクトルを求める。
|
○03-02 変換行列の要素を操作する
Matrixインスタンスが表す変換行列は、3行×3列の数学的な行列です。行列の各要素(「成分」とも呼ばれます)は、以下のように定められます。各要素の値は、Matrixインスタンスを作成するときに引数として指定できます。また、Matrixクラスに同じ名前のプロパティとしても定義されています(シンタックス03-003)。なお、変換行列の最後の第3行は、Matrixクラスでは要素の値が([0 0 1]と)決まっていて、操作対象にはなりません。
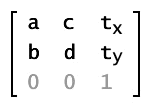
シンタックス03-003■Matrixクラスの変換行列とその要素
|
Matrix()コンストラクタ
|
|
文法
|
Matrix(a:Number = 1, b:Number = 0, c:Number = 0, d:Number = 1, tx:Number = 0, ty:Number = 0)
|
|
概要
|
指定された引数が要素(成分)となる3行×3列の変換行列のMatrixインスタンスを生成する。変換行列は要素が図03-008左図のように定められる。引数なしに作成されたデフォルトのMatrixインスタンスは、対角要素が1で他の要素が0の単位行列になる(図03-008右図)。
図03-008■変換行列の要素と単位行列
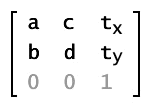
変換行列
|

単位行列 |
|
3行×3列の変換行列の要素(左図)。単位行列は、対角要素が1で他の要素が0(右図)。
|
ただし、変換行列の第3行目の要素は決まっていて、操作できない。
|
|
引数
|
デフォルトのDisplayObjectインスタンス対して加える変換についての下表03-001で示される値。なお、各引数は、以下の同名のプロパティの値となる。
表03-001■6つの引数と設定値
|
引数
|
値
|
デフォルト値
|
|
a:Number = 0
|
水平方向の拡大・縮小ピクセル数/デフォルトの幅のピクセル数
|
1 |
|
b:Number = 0
|
垂直方向の傾斜ピクセル数/デフォルトの幅のピクセル数
|
0 |
|
c:Number = 0
|
水平方向の傾斜ピクセル数/デフォルトの高さのピクセル数
|
0 |
|
d:Number = 0
|
垂直方向の拡大・縮小ピクセル数/デフォルトの高さのピクセル数
|
1 |
|
tx:Number = 0
|
親インスタンスの基準点からの水平方向の移動ピクセル数
|
0 |
|
ty:Number = 0
|
親インスタンスの基準点からの垂直方向の移動ピクセル数
|
0 |
|
|
Matrix.aプロパティ
|
|
文法
|
a:Number
|
|
プロパティ値
|
Matrixオブジェクトが表す変換行列の中の水平方向の拡大・縮小比率。もとのDisplayObjectインスタンス(デフォルト状態)の幅に対する割合で示す。 |
|
Matrix.bプロパティ
|
|
文法
|
b:Number
|
|
プロパティ値
|
Matrixオブジェクトが表す変換行列の中の垂直方向の傾斜比率。もとのDisplayObjectインスタンス(デフォルト状態)の幅に対する割合で示す。 |
|
Matrix.dプロパティ
|
|
文法
|
d:Number
|
|
プロパティ値
|
Matrixオブジェクトが表す変換行列の中の垂直方向の拡大・縮小比率。もとのDisplayObjectインスタンス(デフォルト状態)の高さに対する割合で示す。 |
|
Matrix.dプロパティ
|
|
文法
|
d:Number
|
|
プロパティ値
|
Matrixオブジェクトが表す変換行列の中の垂直方向の拡大・縮小比率。もとのDisplayObjectインスタンス(デフォルト状態)の高さに対する割合で示す。 |
|
Matrix.txプロパティ
|
|
文法
|
tx:Number
|
|
プロパティ値
|
Matrixオブジェクトが表す変換行列の中の水平方向の移動ピクセル位置。DisplayObjectインスタンスが配置された親インスタンスの基準点を原点とする。 |
|
Matrix.tyプロパティ
|
|
文法
|
ty:Number
|
|
プロパティ値
|
Matrixオブジェクトが表す変換行列の中の垂直方向の移動ピクセル位置。DisplayObjectインスタンスが配置された親インスタンスの基準点を原点とする。 |
|
Word 03-001■行列
行列とは、いくつかの値を表のように、行と列の長方形に並べたものです。その両端を()または[]でくくって表します。加減算や乗算などの演算法則が定められています。前述Tips 03-001のとおり、乗算は交換法則が成立ちません。詳しくは、後述数学編をご参照ください。
|
|
Maniac! 03-001■変換行列の行数と列数
2次元平面における拡大・縮小や回転は、2行×2列の行列(要素a、b、c、d)で変換できます。しかし、変換のとき、前述のとおり原点(0, 0)が動かせません。そこで、第3列目(要素txとty)を加えて、平行移動の変換ができるようにしたのです。平行移動を組合わせることにより、原点以外を起点とした変換が可能になりました。
なお、行列による変換は行数と列数が等しい方が扱いやすいため、要素の固定された([0 0 1]の)第3行目が加えられました。行数と列数が等しい行列は「正方行列」と呼ばれます。
|
Matrixインスタンスをtrace()関数で[出力]すると、変換行列の要素となるMatrixクラスのプロパティ値が表示されます。たとえば、前掲スクリプト03-001に以下のようなtrace()関数のステートメントを加えて、変換のためのMatrixクラスのメソッド呼出しのたびにMatrixインスタンスを[出力]すると、つぎのように各値が表示されます(図03-009)。
|
var myMatrix:Matrix = my_mc.transform.matrix;
trace(myMatrix);
// 出力: (a=1, b=0, c=0, d=1, tx=0, ty=0)
myMatrix.scale(1.5, 1.2);
trace(myMatrix);
// 出力: (a=1.5, b=0, c=0, d=1.2, tx=0, ty=0)
myMatrix.rotate(Math.PI/6);
trace(myMatrix);
// 出力: (a=1.299038105676658, b=0.7499999999999999, c=-0.5999999999999999, d=1.0392304845413265, tx=0, ty=0)
myMatrix.translate(80, 40);
trace(myMatrix);
// 出力: (a=1.299038105676658, b=0.7499999999999999, c=-0.5999999999999999, d=1.0392304845413265, tx=80, ty=40)
my_mc.transform.matrix = myMatrix;
|
図03-009■Matrixインスタンスの[出力]は変換行列のプロパティ値を示す
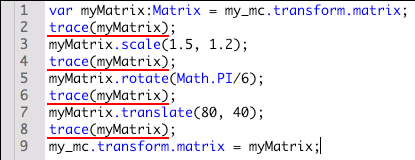

|
Matrixクラスの各メソッドを適用する前後の変換行列の各プロパティ値が[出力]されている。
|
オーサリング(ムービー作成)時にタイムラインに配置されたインスタンスも、基本的にMatrixオブジェクトはもっています。たとえば、スクリプト03-001とほぼ同じ変形を、スクリプトでなく[プロパティ]インスペクタや[変形]パネルで行ってみます(図03-010)。このインスタンスのDisplayObject.transformプロパティから参照したTransform.matrixプロパティの値を[出力]すると、つぎのようにスクリプト03-001の結果とほぼ同じ値が表示されます(多少の誤差は生じます)。
(a=1.299041748046875, b=0.7500152587890625, c=-0.5999908447265625, d=1.039215087890625, tx=80, ty=40)
図03-010■オーサリング時にパネルなどでインスタンスを変形
|
オーサリング時に変形したインスタンスも、Matrixオブジェクトをもつ。
|
Matrixクラスのコンストラクタを引数なしに呼出すと、デフォルト(単位行列)のオブジェクトが生成されます(前掲シンタックス03-003)。DisplayObjectインスタンスのDisplayObject.transformプロパティから参照したTransform.matrixプロパティにデフォルトのMatrixオブジェクトを設定すると、インスタンスは伸縮が実寸(100%)、回転なし(0度)、そして位置は親タイムラインの基準点にあるデフォルト状態になります。
たとえば、タイムラインに前掲図03-010のように変形したインスタンスmy_mcを置いて、以下のスクリプト03-003をそのフレームアクションとして記述すると、初めインスタンスは変形される前のデフォルト状態で表示されます。そして、インスタンスをクリックすれば、タイムライン上で設定した変形が改めて適用されます(図03-011)。
スクリプト03-003■変形したインスタンスを一旦デフォルト状態にしてクリックでもとに戻す
// フレームアクション
// 変形したインスタンスmy_mcを配置
- var myMatrix:Matrix = my_mc.transform.matrix;
- my_mc.transform.matrix = new Matrix();
- my_mc.addEventListener(MouseEvent.CLICK, xTransform);
- function xTransform(eventObject:MouseEvent):void {
- my_mc.transform.matrix = myMatrix;
- }
|
図03-011■デフォルト状態になったインスタンスがクリックするともとのとおり変形される
 |
|
↓インスタンスをクリック
|
 |
|
予め変形されていたインスタンスは、初めデフォルト状態で表示される。インスタンスをクリックすると、もとの変形が改めて適用される。
|
まず、スクリプト第1行目では、変形したMovieClipインスタンス(my_mc)のDisplayObjectインスタンスのDisplayObject.transformプロパティからTransform.matrixプロパティを参照して、そのMatrixオブジェクトを変数(myMatrix)に保持しておきます。
つぎに、スクリプト第2行目で、引数なしに呼出したMatrixコンストラクタでインスタンスを生成して、プロパティに代入します。これで、MovieClipインスタンスはデフォルト状態に設定されます。
そして、第3行目でMovieClipインスタンスのInteractiveObject.clickイベント(定数MouseEvent.CLICK)にリスナー関数xTransform()を登録します。第4〜6行目に定義されたリスナー関数xTransform()は、第1行目で変数に保持しておいたMatrixオブジェクトをMovieClipインスタンスのDisplayObject.transformプロパティのTransform.matrixプロパティに改めて設定し直します。
これで、初めにデフォルト状態で表示されたMovieClipインスタンスが、マウスクリックで改めて変形された形状に戻ります。
多くの場合、2次元平面の座標変換は、Matrixクラスのメソッドおよびその組合わせで行えます。ただ、それらのメソッドは使わず、変換行列の要素のプロパティを用いても、それらすべての変換はできます。メソッドによる変換と変換行列の要素との対応を、下表03-002にまとめておきます。
表03-002■変換行列のプロパティ値とその適用結果
|
変換
|
メソッド
|
変換行列の値
|
変換結果
|
|
デフォルト
|
new Matrix()
|
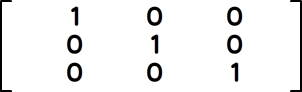
|

|
|
平行移動
|
translate(tx:Number, ty:Number):void
|
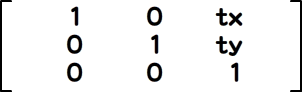
|

|
|
拡大・縮小
|
scale(a:Number, d:Number):void
|
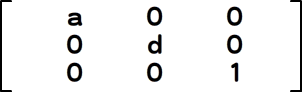
|

|
|
回転
|
rotate(θ:Number):void
|
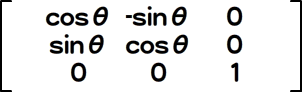
|

|
|
傾斜
|
−
|
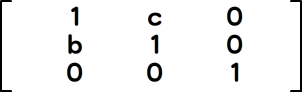
|

|
表03-002に記載したとおり、回転の変換については、角度を直接設定すべき変換行列の要素はありません。Matrix.a/Matrix.b/Matrix.c/Matrix.dの各プロパティにそれぞれcosθ、sinθ、-sinθ、cosθの値を設定して、θ回転するMatrixオブジェクトをつくります。さらにひとつ注意すべきこととして、傾斜の変換だけは、Matrixクラスにメソッドが備わっておらず、変換行列の要素を操作する必要があります。傾斜については、つぎに項を改めます。
|
Tips 03-003■[ヘルプ]のMatrixクラスの説明における変換行列の誤り
[ヘルプ]の[ActionScript 3.0言語およびコンポーネントリファレンス]で[Matrixクラス]の説明を見ると、本稿執筆時点では変換行列の記載で要素となるbとcのプロパティの位置が入れ違っています(表03-003)。正しくは上記の表03-002に掲載した変換行列のとおりです。
表03-003■[ヘルプ]で誤って掲載されている変換行列
|
○03-03 傾斜を加える
前述のとおり、プロパティMatrix.bやMatrix.cにそれぞれ垂直あるいは水平傾斜比率を設定すると、インスタンスに傾斜が加えられます(前掲シンタックス03-003参照)。これらの比率を計算するときに分母となるDisplayObjectインスタンスの幅や高さは、デフォルト時の値であることにご注意ください。
垂直傾斜比率(Matrix.b) = 垂直傾斜ピクセル数/デフォルトの幅
水平傾斜比率(Matrix.c) = 水平傾斜ピクセル数/デフォルトの高さ
すると、Matrix.a/Matrix.b/Matrix.c/Matrix.dの各プロパティをそれぞれ計算すれば、矩形のDisplayObjectインスタンスを任意の平行四辺形に変換できます。たとえば、下図03-012のようにデフォルトで100×100ピクセルのインスタンスmy_mcが親タイムラインの基準点O(0, 0)に配置されているとして、右上角座標P(100, 0)をP'(120, 30)に、左下角座標Q(0, 100)はQ'(50, 150)の平行四辺形に変換するとします。
図03-012■矩形のインスタンスを任意の平行四辺形に変換

|
右上隅座標P(100, 0)をP'(120, 30)に、左下隅座標Q(0, 100)はQ'(50, 150)の平行四辺形に変換する。
|
変換行列の要素となる各プロパティの値は、つぎのように求められます。
水平伸縮比率(Matrix.a) = 120/OP = 120/100 = 1.2
垂直傾斜比率(Matrix.b) = 30/OP = 30/100 = 0.3
水平傾斜比率(Matrix.c) = 50/OQ = 50/100 = 0.5
垂直伸縮比率(Matrix.d) = 150/OQ = 150/100 = 1.5
矩形のインスタンスを平行四辺形に変換する処理は、後の拡張を考えて関数xTransformPoints()として以下のように定義します。第1引数には変換するMovieClipインスタンス、第2ならびに第3引数には右上角と左下角の座標をともにPointインスタンスで渡します(図03-013)。
xTransformPoints(my_mc, new Point(120, 30), new Point(50, 150));
function xTransformPoints(_mc:MovieClip, point0:Point, point1:Point):void {
var myMatrix:Matrix = _mc.transform.matrix;
var nWidth:Number = _mc.width;
var nHeight:Number = _mc.height;
myMatrix.a = (point0.x) / nWidth;
myMatrix.b = (point0.y) / nWidth;
myMatrix.c = (point1.x) / nHeight;
myMatrix.d = (point1.y) / nHeight;
_mc.transform.matrix = myMatrix;
}
|
図03-013■定義した関数で矩形のインスタンスを平行四辺形に変換

|
関数には、第1引数に変換するMovieClipインスタンス、第2ならびに第3引数として右上角と左下角の座標をともにPointインスタンスで渡す。
|
|
Word 03-002■アフィン変換
Matrixクラスが行う座標空間の変換を、「アフィン変換」といいます。アフィン変換では、もとの座標空間で平行な2直線は、変換後も平行になります。つまり、矩形を平行四辺形には変換できても、遠近法の表現された台形にすることはできません。
|
さらに、プロパティMatrix.txとMatrix.tyの操作を加えれば、平行四辺形に変換したインスタンスを任意の場所に置くことができます。そこで、矩形のインスタンスの右上と左上,および左下の3つの角にドラッグできるポイントとなるインスタンスを配置し、それらの座標に合わせて矩形のインスタンスの任意の平行四辺形に変換してみます(図03-014)。
図03-014■ドラッグした3つのポイントの座標に合わせて矩形のインスタンスを平行四辺形に変換

|
矩形のインスタンスの3つの角にあるポイントをドラッグすると、その座標に合わせてインスタンスが任意の平行四辺形に変換される。
|
矩形のインスタンスmy_mcを配置したタイムラインに記述するフレームアクションは、スクリプト03-005として後に掲げます(以下の解説で示す行番号はこのスクリプト03-005にもとづきます)。まずは、MovieClipインスタンスのDisplayObject.transformプロパティから参照したTransform.matrixプロパティに変換を加える関数xTransformPoints()の拡張から考えましょう。
- function xTransformPoints(_mc:MovieClip, point0:Point, point1:Point, point2:Point):void {
// var myMatrix:Matrix = _mc.transform.matrix;
- var myMatrix:Matrix = new Matrix();
- _mc.transform.matrix = myMatrix;
- var nWidth:Number = _mc.width;
- var nHeight:Number = _mc.height;
- var point1_0:Point = point0.subtract(point1);
- var point1_2:Point = point2.subtract(point1);
- myMatrix.a = (point1_0.x) / nWidth;
- myMatrix.b = (point1_0.y) / nWidth;
- myMatrix.c = (point1_2.x) / nHeight;
- myMatrix.d = (point1_2.y) / nHeight;
- myMatrix.tx = point1.x;
- myMatrix.ty = point1.y;
- _mc.transform.matrix = myMatrix;
- }
|
第1に、関数の引数として座標を示すPointインスタンスがひとつ増えています(スクリプト第7行目)。インスタンスの位置の移動が加わったためで、Pointインスタンスの座標の引数は、反時計回りに右上(point0)、左上(point1)、左下(point2)の順序で渡します。
第2に、左上角の座標(point1)が動きますので、デフォルトの幅や高さ、あるいは伸縮や傾斜のピクセル数は、左上角を起点として計算しなければなりません。そこで、スクリプト第12〜13行目で、Point.subtract()メソッドにより左上角から見た右上角(point1_0)と左下角(point1_2)のベクトル(Pointインスタンス)を求めています(シンタックス03-002参照)。そのうえで、スクリプト第14〜17行目は、これらのPointインスタンスから各プロパティの値を計算して、設定しています。
第3にスクリプト第8〜9行目で、インスタンスのプロパティDisplayObject.transformから参照したTransform.matrixに、デフォルトのMatrixインスタンス(単位行列)を設定していることに注目してください。これは、伸縮および傾斜の比率を計算するときのインスタンスの幅や高さが、デフォルト状態の値でなければならないからです(コメントアウトした修正前のステートメントは、MovieClipインスタンスがデフォルト状態であることを前提としていました)。
関数xTransformPoints()に、第1引数として矩形のMovieClipインスタンス、第2から第4引数に右上、左上、左下の3つの角の座標をPointインスタンスで渡して呼出せば、それらの座標に合わせて矩形のインスタンスが平行四辺形に変換されます(図03-014)。
xTransformPoints(my_mc, new Point(160, 50), new Point(40, 20), new Point(90, 170));
図03-014■指定した3つの座標に合わせて矩形のインスタンスを平行四辺形に変換

|
関数に右上、左上、左下の3つの角の座標をPointインスタンスで渡すと、指定した矩形のインスタンスがその座標に合わせて平行四辺形に変換される。
|
矩形のインスタンスの3つの角に配置してドラッグするインスタンスについては、そのシンボルにフレームアクションを記述します(図03-015)。処理のおもな内容は、そのインスタンスをドラッグする操作と、ドラッグしている間親タイムラインに定義した関数xTransform()を呼出し続けることです(スクリプト03-004)。
図03-015■ドラッグするポイントのシンボルにフレームアクションを記述

|
処理のおもな内容は、そのインスタンスのドラッグと、ドラッグしている間親タイムラインに定義した関数xTransform()を呼出し続けること。
|
スクリプト03-004■インスタンスのドラッグ操作と親タイムラインの関数呼出し
// フレームアクション
// MovieClip: ドラッグするポイントのシンボル
- buttonMode = true;
- addEventListener(MouseEvent.MOUSE_DOWN, xPress);
- function xPress(eventObject:MouseEvent):void {
- stage.addEventListener(MouseEvent.MOUSE_UP, xRelease);
- addEventListener(Event.ENTER_FRAME, xUpdate);
- startDrag();
- }
- function xRelease(eventObject:MouseEvent):void {
- stage.removeEventListener(MouseEvent.MOUSE_UP, xRelease);
- removeEventListener(Event.ENTER_FRAME, xUpdate);
- stopDrag();
- xUpdate();
- }
- function xUpdate(eventObject:Event=null):void {
- MovieClip(parent).xTransform();
- }
|
まず、インスタンスに対するInteractiveObject.mouseDownイベント(定数MouseEvent.MOUSE_DOWN)のリスナー関数xPress()で、インスタンスのドラッグを始めるとともに(シンタックス02-002「Sprite.startDrag()とSprite.stopDrag()メソッド」参照)、イベントInteractiveObject.mouseUp(定数MouseEvent.MOUSE_UP)とDisplayObject.enterFrame(定数Event.ENTER_FRAME)にそれぞれリスナー関数xReleaseとxUpdate()を登録します。
リスナー関数xUpdate()はDisplayObject.enterFrameイベントに登録されていますので、インスタンスをドラッグしている間繰返し呼出されます。そして、関数xUpdate()は、親タイムラインの関数はxTransform()を呼出します。関数xTransform()には、ドラッグしたインスタンスの座標に合わせて矩形のインスタンスを平行四辺形に変換する処理が定義されます。
リスナー関数xRelease()は、マウスボタンを放したとき、ドラッグを終える処理です。関数xPress()で登録したイベントリスナーを削除しています。なお、マウスボタンを放す操作はインスタンス上かどうかを問わないため、Stageオブジェクト(DisplayObject.stage)にイベントリスナーとして登録しました。
|
Tips 03-004■親のフレームアクションで定義した関数にアクセスする − キャスト
親のタイムラインには、プロパティDisplayObject.parentでアクセスできます。ところが、親のフレームアクションに定義した関数(xTransform)を、DisplayObject.parentプロパティの参照に対して呼出そうとすると、[コンパイルエラー]が生じます。エラーの説明には、その関数(xTransform)は「未定義の可能性」があるとされています(図03-016)。
図03-016■DisplayObject.parentから親タイムラインに定義した関数を呼出すと[コンパイルエラー]

|
[コンパイルエラー]パネルには、その関数は「未定義の可能性」があると説明されている。
|
DisplayObject.parentプロパティの値は、DisplayObjectでデータ型が指定されています。[ヘルプ]の[ActionScript 3.0言語およびコンポーネントリファレンス]で[DisplayObject]クラスを見ても、当然カスタム関数(xTransform)は載っていません。「未定義」というのは、つまりクラスに定義されていないということを意味します。
しかし、もちろんMovieClipクラスのインスタンスであるタイムラインには、カスタム関数を定義することができます(このように変数や関数が加えられるクラスを、dynamicなクラスといいます)。このような場合には、DisplayObject.parentプロパティの参照がMovieClipクラスであることを限定すれば、カスタムクラスにアクセスできるようになります。そのためには、値をつぎのようにして限定するクラスに変換します。この変換の操作を「キャスト」と呼びます。
限定するクラス(値)
前記スクリプト03-004の第15行目は、DisplayObject.parentプロパティの参照をMovieClipクラスにキャストしています。
|
矩形のインスタンスと3つのポイントが配置されたフレームアクションに関数xTransform()を定義して、スクリプト03-005は完成です。スクリプト第2〜4行目で3つのポイントのインスタンスの座標からPointインスタンスを生成し、第5行目に矩形のインスタンスとそれら3つのPointインスタンスを引数としてxTransformPoints()が呼出されています。
スクリプト03-005■ドラッグした3つのポイントに合わせて矩形のインスタンスを変換する
// フレームアクション
// 変形したインスタンスmy_mcを配置
- function xTransform():void {
- var point0:Point = new Point(point0_mc.x, point0_mc.y);
- var point1:Point = new Point(point1_mc.x, point1_mc.y);
- var point2:Point = new Point(point2_mc.x, point2_mc.y);
- xTransformPoints(my_mc, point0, point1, point2);
- }
- function xTransformPoints(_mc:MovieClip, point0:Point, point1:Point, point2:Point):void {
- var myMatrix:Matrix = new Matrix();
- _mc.transform.matrix = myMatrix;
- var nWidth:Number = _mc.width;
- var nHeight:Number = _mc.height;
- var point1_0:Point = point0.subtract(point1);
- var point1_2:Point = point2.subtract(point1);
- myMatrix.a = (point1_0.x) / nWidth;
- myMatrix.b = (point1_0.y) / nWidth;
- myMatrix.c = (point1_2.x) / nHeight;
- myMatrix.d = (point1_2.y) / nHeight;
- myMatrix.tx = point1.x;
- myMatrix.ty = point1.y;
- _mc.transform.matrix = myMatrix;
- }
|
これで、3つのポイントのインスタンス(point0_mc〜point2_mc)をドラッグすれば、それらの座標に合わせて矩形のインスタンス(my_mc)が自由な平行四辺形に変換されます(図03-017)。
図03-017■ポイントをドラッグするとその座標に合わせて矩形のインスタンスが平行四辺形に変換される

|
矩形のインスタンスの3つの角にあるポイントをドラッグすると、その座標に合わせてインスタンスが任意の平行四辺形に変換される。
|
3次元の変換行列は04「3次元座標空間でDisplayObjectインスタンスを扱う − Matrix3Dクラス」で、ベクトルは06「3次元空間の座標を扱う − Vector3Dクラス」で扱います。これらのクラスの備える具体的なプロパティやメソッドは、MatrixやPointクラスとは異なっています。しかし、2次元のベクトルと行列の考え方は、次元がひとつ増えて3次元になっても、基本的に変わりません。ですから、この2次元平面の理解を確かなものにしておきましょう。
○Column 03 Transformクラスのオブジェクトへのアクセス
DisplayObject.transformプロパティで参照できるTransformオブジェクトには、座標空間に関わるプロパティとして、すでにご紹介したTransform.perspectiveProjection(シンタックス02-001「消失点を操作するためのプロパティ」)やTransform.matrix(シンタックス03-001)のほか、後述するTransform.matrix3Dがあります。これらのプロパティから参照されるオブジェクトの操作の仕方は、少しずつ異なります。
まず、Matrixオブジェクトは、03-01「Matrixクラスのメソッドを使った座標変換」の「Matrixオブジェクトを使ったDisplayObjectインスタンスの変換の手順」でご説明したとおり、つねに「MatrixインスタンスをDisplayObject.transformプロパティのTransform.matrixプロパティに設定する」必要があります(図03-018)。
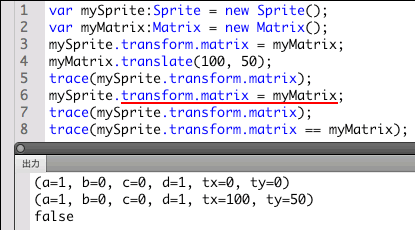
以下のスクリプト第3行目でデフォルトのMatrixインスタンスをTransform.matrixプロパティに設定し、第4行目でそのインスタンスに移動の変換を加えても、DisplayObject(Sprite)インスタンスから参照したMatrixオブジェクトは何も変わっていません(第5行目のtrace()関数の[出力]がデフォルトのMatixオブジェクトのまま)。
スクリプト第6行目で、DisplayObject.transformから参照したTransform.matrixプロパティに改めてMatrixオブジェクトを設定して初めて、その変換がインスタンスに適用されます(第7行目のtrace()関数の[出力]参照)。
【Matrixオブジェクトのテスト】
- var mySprite:Sprite = new Sprite();
- var myMatrix:Matrix = new Matrix();
- mySprite.transform.matrix = myMatrix;
- myMatrix.translate(100, 50);
- trace(mySprite.transform.matrix);
// 出力: (a=1, b=0, c=0, d=1, tx=0, ty=0)
- mySprite.transform.matrix = myMatrix;
- trace(mySprite.transform.matrix);
// 出力: (a=1, b=0, c=0, d=1, tx=100, ty=50)
- trace(mySprite.transform.matrix == myMatrix);
// 出力: false
|
図03-018■MatrixオブジェクトはDisplayObject.transformのTransform.matrixに必ず設定する
|
DisplayObject.transformから参照したTransform.matrixプロパティにMatrixオブジェクトを設定して初めて、その変換がインスタンスに適用される。
|
つぎに、後述するMatrix3Dオブジェクトは、DisplayObject.transformのTransform.matrix3Dプロパティに対する参照を取得すれば足ります。参照したMatrix3Dオブジェクトを操作すれば、その変換はDisplayObjectインスタンスに直ちに適用されます。したがって、Matrix3Dオブジェクトを改めてDisplayObject.transformのTransform.matrix3Dプロパティに設定し直す必要がありません(図03-019)。
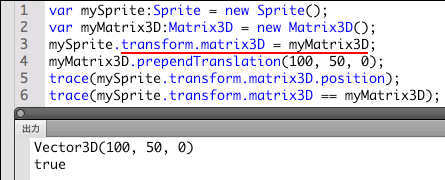
以下のスクリプト第3行目で、デフォルトのMatrix3DインスタンスをTransform.matrix3Dプロパティに設定し、第4行目でそのインスタンスに移動(Matrix3D.prependTranslation()メソッド)の変換を加えると、DisplayObject(Sprite)インスタンスから参照したTransform.matrix3Dプロパティのオブジェクトも値が変わります(第5行目のtrace()関数は、Matrix3Dオブジェクトのxyz座標を表すMatrix3D.positionプロパティを[出力])。つまり、その変換がDisplayObject(Sprite)インスタンスに適用されます。なお、Matrix3Dクラスについては、後述04「3次元座標空間でDisplayObjectインスタンスを扱う − Matrix3Dクラス」で詳しく解説します。
【Matrix3Dオブジェクトのテスト】
- var mySprite:Sprite = new Sprite();
- var myMatrix3D:Matrix3D = new Matrix3D();
- mySprite.transform.matrix3D = myMatrix3D;
- myMatrix3D.prependTranslation(100, 50, 0);
- trace(mySprite.transform.matrix3D.position);
// 出力: Vector3D(100, 50, 0)
- trace(mySprite.transform.matrix3D == myMatrix3D);
// 出力: true
|
図03-019■Matrix3DオブジェクトはDisplayObject.transformのTransform.matrix3Dに対する参照を取得すればよい
|
DisplayObject.transformのTransform.matrixプロパティに対するMatrixオブジェクトの参照を得れば、そのオブジェクトへの変換が直ちにインスタンスに適用される。
|
最後のPerspectiveProjectionオブジェクトは、少し振舞いが変わっています(図03-020)。
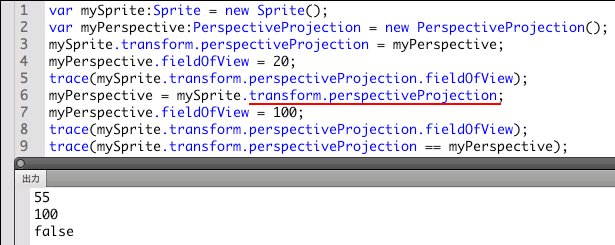
以下のスクリプト第3行目で、デフォルトのPerspectiveProjectionインスタンスをTransform.perspectiveProjectionプロパティに設定し、第4行目でそのインスタンスの視野角(PerspectiveProjection.fieldOfViewプロパティ)を設定しても、DisplayObject(Sprite)インスタンスから参照したTransform.perspectiveProjectionプロパティのオブジェクトは視野角が変わりません(第5行目のtrace()関数の[出力]参照)。この結果は、Matrixオブジェクトの場合と同じです。
他方、スクリプト第6行目で、Transform.perspectiveProjectionプロパティの参照をひとたび変数(myPerspective)に取ると、第7行目でその変数のオブジェクトに対して設定した視野角の値が、DisplayObject(Sprite)インスタンスにそのまま設定されます(第8行目のtrace()関数の[出力]参照)。つまり、Matrix3Dオブジェクトと同じく、変数にDisplayObject.transformのTransform.perspectiveProjectionプロパティの参照が得られたことを意味します。
【PerspectiveProjectionオブジェクトのテスト】
- var mySprite:Sprite = new Sprite();
- var myPerspective:PerspectiveProjection = new PerspectiveProjection();
- mySprite.transform.perspectiveProjection = myPerspective;
- myPerspective.fieldOfView = 20;
- trace(mySprite.transform.perspectiveProjection.fieldOfView);
// 出力: 55
- myPerspective = mySprite.transform.perspectiveProjection;
- myPerspective.fieldOfView = 100;
- trace(mySprite.transform.perspectiveProjection.fieldOfView);
// 出力: 100
- trace(mySprite.transform.perspectiveProjection == myPerspective);
// 出力: false
|
図03-020■PerspectiveProjectionオブジェクトはDisplayObject.transformのTransform.perspectiveProjectionから取得する必要がある
|
DisplayObject.transformのTransform.perspectiveProjectionプロパティからPerspectiveProjectionオブジェクトの参照を得れば、そのオブジェクトへの操作がインスタンスに適用される。
|
|
Tips 03-005■オブジェクトの参照と複製
オブジェクトを変数に代入すると、その参照が渡されます。Transform.matrix3DプロパティのMatrix3Dオブジェクトは、この参照渡しが行われます。したがって、上記「Matrix3Dオブジェクトのテスト」のスクリプト第4行目で、同じオブジェクトへの参照をもつ変数(myMatrix3D)が操作されると、Transform.matrix3Dプロパティの参照するMatrix3Dオブジェクトに変換が加わりました。
他方、Transform.matrixプロパティには、Matrixオブジェクトの参照が渡されるのでなく、オブジェクトは複製されて別に設定されるようです。前記「Matrixオブジェクトのテスト」のスクリプト第8行目で、Transform.matrixプロパティと変数のMatrixオブジェクトが等しいかどうかを確かめると、falseと評価されます。「Matrix3Dオブジェクトのテスト」のスクリプト第6行目では、同様な評価がtrueとされることと比べてみましょう。
なお、Transform.perspectiveProjectionプロパティも、参照渡しではなさそうです(「PerspectiveProjectionオブジェクトのテスト」のスクリプト第9行目の[出力]参照)。少し変わった振舞いはあるものの、基本的にはTransform.matrixプロパティのMatrixオブジェクトと同じと考えてよいでしょう。
|
[Prev/Next]
作成者: 野中文雄
作成日: 2009年10月27日











