サイトトップ
Director Flash 書籍 業務内容 プロフィール

ActionScript 3.0 for 3D

□06 3次元空間の座標を扱う − Vector3Dクラス

Vector3Dクラスは、3次元空間の座標をおもに扱います。Vector3Dクラスには、3次元座標空間における位置ベクトル(x, y, z)の成分(要素)となるVector3D.xやVector3D.y、およびVector3D.zプロパティに加えて、4つめの成分としてVector3D.wプロパティがあります(シンタックス06-001)、つまり、Vector3Dインスタンスは4次元のベクトルです(図06-001)。そして、Vector3Dクラスには、インスタンスが表すベクトルに対して加減算やスカラー倍、内積・外積などを計算するメソッドが備わっています。

Tips 06-001■Vector3Dクラスはなぜ4次元のベクトルなのか
Matrix3Dクラスが表す3次元座標空間の変換行列は、4行×4列でした(シンタックス04-011)。その4行×4列の変換行列と演算を行うため、Vector3Dクラスのベクトルもそれに合わせて4次元になっています。

Maniac! 06-001■[ヘルプ]のVector3Dクラスの説明
[ヘルプ]の[ActionScript 3.0言語およびコンポーネントリファレンス]で[Vector3D]に、「Vector3Dクラスは、極座標x、y、および z を使用」すると説明しているのは(本稿執筆時)、邦訳の誤りでしょう。英語の原文は"Cartesian coordinates"ですので、「極座標」ではなく「デカルト座標」つまり直交座標を意味します。極座標は、位置を原点からの距離および軸となす角度で表します。

○06-01 Vector3Dインスタンスの座標変換とワイヤーフレームの描画
前述のとおり、Vector3Dクラスは4次元のベクトルを表します。とはいえ、第4成分(要素)はオプションです。3次元座標の扱いは、おもにxyz座標値の3成分で行われることが多いでしょう。まず、基本となるVector3Dクラスのコンストラクタメソッドと座標(成分)のプロパティは、以下のシンタックス04-001のとおりです。

シンタックス06-001■Vector3Dクラスのコンストラクタメソッドと座標(成分)のプロパティ
Vector3D()コンストラクタ
文法 Vector3D(x:Number = 0, y:Number = 0, z:Number = 0, w:Number = 0)
概要

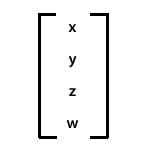
指定した座標(成分)値が与えられたVector3Dインスタンスを生成する。インスタンスは3次元のxyz座標値に加えて、オプションのw値を成分にもつ4次元ベクトルで表される(図06-001)。

図06-001■Vector3Dインスタンスが表す4次元ベクトル

xyz座標値に加えて、w値を成分にもつ4次元ベクトルで表される。
引数

x:Number ― インスタンスのx座標値または第1成分値。デフォルト値は0。

y:Number ― インスタンスのy座標値または第2成分値。デフォルト値は0。

z:Number ― インスタンスのz座標値または第3成分値。デフォルト値は0。

w:Number ― インスタンスのオプションのw値または第4成分値。透視投影比率などを納める。デフォルト値は0。
Vector3D.x/y/z/wプロパティ
文法 x:Number
y:Number
z:Number
w:Number
プロパティ値

Vector3Dインスタンスの各座標のプロパティ値またはインスタンスが表すベクトルの成分値。

ただし、Vector3D.wプロパティは3次元座標とは別のオプションとして用いられる。透視投影比率を設定すると、Vector3D.project()メソッドによりxyz座標値を除する値となる。

Matrix3D.decompose()とMatrix3D.recompose()メソッド(前掲シンタックス04-011)が扱う平行移動と回転および伸縮の3つのエレメントを納めたVectorオブジェクトは、Vector3Dをベース型とする。そのインデックス1の回転を示すVector3Dオブジェクトには、オイラー角や軸角度(前掲Column 04「3次元座標空間における回転について」の「軸角度による回転」参照)、あるいは四元数(後述数学編「四元数(クォータニオン)」参照)の表し方で各成分値を決める。

例によって、Vector3Dインスタンスを回してみたいと思います。インスタンスの生成は、コンストラクタメソッドにxyz座標値を渡すだけです。座標単位で3次元の操作をしようとすれば、インスタンスの数はすぐに増えてしまいます。そこで、前章05「配列に型指定を加えた厳格なクラス − Vectorクラス」で学んだVectorクラスにまとめて納めることにします。手始めに、正方形を1面つくります。座標は1辺の半分の長さを変数nUnitとして、原点を中心に4頂点を下図06-002のように定めます。z座標値はいずれも0です。

図06-002■3次元空間に正方形の座標を定める
1辺の半分の長さを変数nUnitとして、原点を中心に4頂点を定める。z座標値は0。

1辺の長さを100ピクセルとすると、以下のフレームアクションで4頂点のVector3Dオブジェクトが、上図06-002に示した頂点番号0〜3の順序でVectorインスタンスに納められます。最後のステートメントに確認のため加えたtrace()関数により、エレメントの座標値が[出力]パネルにつぎのように表示されます。

Vector3D(-50, -50, 0),Vector3D(50, -50, 0),Vector3D(50, 50, 0),Vector3D(-50, 50, 0)

var nUnit:Number = 100 / 2;
var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
vertices.push(new Vector3D(-nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, nUnit, 0));
vertices.push(new Vector3D(-nUnit, nUnit, 0));
trace(vertices);   // 確認用

Vector3Dクラスを学ぼうとするときに少し困るのは、そのままでは目に見えないことです。trace()関数の[出力]では、細かな動きまでは追いきれません。そこで4頂点を線で結んだいわゆる「ワイヤーフレーム」で描画することにします。描画には、Graphicsクラスのメソッドを使います。もっとも、ご紹介するシンタックス06-002の線描のプロパティとメソッドは、Flash Player 9から備わっています。つまり、2次元平面の描画であることにご注意ください。

シンタックス06-002■Spriteインスタンスに対する線描のためのプロパティとメソッド
Sprite.graphicsプロパティ
文法 graphics:Graphics
プロパティ値 [読取り専用] インスタンスがもつGraphicオブジェクト。Graphicsクラスの描画メソッドを使って、インスタンスにシェイプが描ける。
Graphics.lineStyle()メソッド
文法 lineStyle(thickness:Number = NaN, color:uint = 0, alpha:Number = 1.0, pixelHinting:Boolean = false, scaleMode:String = "normal", caps:String = null, joints:String = null, miterLimit:Number = 3):void
概要 現行の描画位置からの線のスタイルを指定する。
引数

thickness:Number ― 線の太さをポイントで示す整数。0〜255の値を指定する。0は極細線。

color:uint ― 線の色を示す正の整数。通常は16進数で表す。デフォルト値は黒(0x000000)。

alpha:Number ― 線の色のアルファ値の比率を示す数値。完全な透明の0から完全な不透明の1までの値で指定する。デフォルト値は1。

pixelHinting:Boolean ― 線の「ヒント」処理を有効にするかどうかのブール(論理)値(図06-003参照)。trueを指定すると、アンカーの位置をピクセルに合わせるので、線がぼやけにくい。デフォルト値はfalse。

scaleMode:String ― 線の「伸縮」のスタイルを指定する文字列(図06-003参照)。通常は、次表06-001のLineScaleModeクラスの定数を用いる。デフォルト値は標準(LineScaleMode.NORMAL)。

表06-001■伸縮のスタイルを指定するLineScaleModeクラスの定数
オプション LineScaleModeクラス定数 値の文字列 説明
標準 LineScaleMode.NORMAL "normal" 線の太さは伸縮する
水平方向 LineScaleMode.HORIZONTAL "horizontal" 水平方向の伸縮に対しては、線の太さは変わらない
垂直方向 LineScaleMode.VERTICAL "vertical" 垂直方向の伸縮に対しては、線の太さは変わらない
なし LineScaleMode.NONE "none" 線の太さは変わらない

caps:String ― パスの「線端」のはみ出す部分のスタイルを指定する文字列(図06-003参照)。通常は、CapsStyleクラスの定数を用いる。なしはCapsStyle.NONE("none")、丸形がCapsStyle.ROUND("round")、角形はCapsStyle.SQUARE("square")。デフォルトの無指定(null)では丸形になる。

joints:String ― 線の角の「結合」のスタイルを指定する文字列(図06-003参照)。通常は、JointStyleクラスの定数を用いる。マイターはJointStyle.MITER("miter")、丸形がJointStyle.ROUND("round")、ベベルはJointStyle.BEVEL("bevel")。デフォルトの無指定(null)では丸形になる。

miterLimit:Number ― 前引数のjointsに「マイター」(定数JointStyle.MITER)を指定したとき、延ばす長さの限度を決める乗数値(図06-003参照)。マイターの長さは、この値を第1引数のthicknessに乗じたピクセル数で切取られる。デフォルト値は3。

図06-003■描画ツールの[プロパティ]インスペクタで設定できる[塗りと線]
Graphics.lineStyle()メソッドの引数の多くは、シェイプを描くツールで[プロパティ]インスペクタに表れる[塗りと線]の設定項目。

[*筆者用参考]「線のカラーと塗りのカラーの調整」、「線の拡大縮小の制御」。
戻り値 引数のエレメントが加えられた後のインスタンスの長さを表す0以上の整数。
Graphics.moveTo()メソッド
文法 moveTo(x:Number, y:Number):void
概要 現行の描画位置を、指定したxy座標に移動する。
引数

x:Number ― Graphicsオブジェクトが属するDisplayObjectインスタンスの基準点から見た水平ピクセル座標値。

y:Number ― Graphicsオブジェクトが属するDisplayObjectインスタンスの基準点から見た垂直ピクセル座標値。
戻り値 なし。
Graphics.lineTo()メソッド
文法 lineTo(x:Number, y:Number):void
概要 現行の描画位置から指定されたxy座標まで直線を描く。
引数

x:Number ― Graphicsオブジェクトが属するDisplayObjectインスタンスの基準点から見た水平ピクセル座標値。

y:Number ― Graphicsオブジェクトが属するDisplayObjectインスタンスの基準点から見た垂直ピクセル座標値。
戻り値 なし。
Graphics.clear()メソッド
文法 clear():void
概要 参照するGraphicオブジェクトの描画をすべて消去し、線と塗りの設定をリセットする。
引数 なし。
戻り値 なし。

Sprite.graphicsプロパティは、読取り専用のオブジェクトです。したがって、その参照を取って、メソッドを呼出します。MovieClipクラスもSpriteクラスを継承しますので、メインタイムラインに直接シェイプを描くこともできます。けれど、描画のためのSpriteインスタンスを別に用意した方が、位置を変えたりするにも扱いやすいでしょう。

直線の描画は、[ペンツール]で描くのと似た手順です。Graphics.lineStyle()メソッドで線のスタイルを決めたうえで、Graphics.moveTo()メソッドで描き始めの位置を定め、Graphics.lineTo()メソッドで線のアンカーを順に結んでいきます。矩形のように閉じた図形を描くには、書き始めのアンカーまで戻って線を結びます。

つぎのフレームアクションは、Spriteインスタンスをステージの中央に生成して、黒の2ポイントの線で100ピクセル四方の正方形を描きます(図06-004)。

var mySprite:Sprite = new Sprite();
var myGraphics:Graphics = mySprite.graphics;
addChild(mySprite);
mySprite.x = stage.stageWidth / 2;
mySprite.y = stage.stageHeight / 2;
myGraphics.lineStyle(2, 0);
myGraphics.moveTo(-50, -50);
myGraphics.lineTo(50, -50);
myGraphics.lineTo(50, 50);
myGraphics.lineTo(-50, 50);
myGraphics.lineTo(-50, -50);

図06-004■ステージ中央に生成したSpriteインスタンスに黒い線で描かれた正方形

ステージの中央に生成されたSpriteインスタンスに、黒い2ポイントの線で100ピクセル四方の正方形が描かれた。

さて、マウスポインタの水平位置に合わせてワイヤーフレームの正方形を水平に回すフレームアクションは、スクリプト06-001として後に掲げています。けれどいきなり回す前に、3次元座標のVector3Dエレメントが納められたVectorインスタンスから正方形を線描する処理を書いてみましょう。

前述のとおり、Graphicsクラスのメソッドは2次元平面にシェイプを描きます。したがって、VectorインスタンスのVector3Dエレメントから、xy座標を取出さなければなりません。その座標値はPointをベース型とする別のVectorインスタンスに入れることにします。それができれば、あとはVectorインスタンスから2次元座標のPointオブジェクトを順に取出して、Graphicsクラスのメソッドで線を描けばよいということです。

後掲スクリプト06-001の中でワイヤーフレームの正方形を描く処理は、つぎのフレームアクションに抜出したとおりです。Vectorインスタンス内のVector3Dエレメントからxy座標を取出して、Pointをベース型とするVectorオブジェクトで返す処理は関数xGetVertices2D()として定義しました。戻されたVectorインスタンスを関数xDrawLines()に渡すと、Pointエレメントのxy座標値からGraphicsクラスのメソッドで線が描かれます。その結果、前掲図06-004と同じく、ステージ中央に100ピクセル四方の正方形が線描されます。

  1. var nUnit:Number = 100 / 2;
  1. var mySprite:Sprite = new Sprite();
  2. var myGraphics:Graphics = mySprite.graphics;
  3. var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
  4. addChild(mySprite);
  5. mySprite.x = stage.stageWidth / 2;
  6. mySprite.y = stage.stageHeight / 2;
  7. vertices.push(new Vector3D(-nUnit, -nUnit, 0));
  8. vertices.push(new Vector3D(nUnit, -nUnit, 0));
  9. vertices.push(new Vector3D(nUnit, nUnit, 0));
  10. vertices.push(new Vector3D(-nUnit, nUnit, 0));
  1. var vertices2D:Vector.<Point> = xGetVertices2D(vertices);
  2. xDrawLines(vertices2D);
  1. function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point> {
  2.   var vertices2D:Vector.<Point> = new Vector.<Point>();
  3.   var nLength:uint = myVertices.length;
  4.   for (var i:uint = 0; i < nLength; i++) {
  5.     var myVector3D:Vector3D = myVertices[i];
  6.     vertices2D.push(new Point(myVector3D.x, myVector3D.y));
  7.   }
  8.   return vertices2D;
  9. }
  10. function xDrawLines(vertices2D:Vector.<Point>):void {
  11.   var nLength:uint = vertices2D.length;
  12.   var myPoint:Point = vertices2D[nLength - 1];
  1.   myGraphics.lineStyle(2, 0);
  2.   myGraphics.moveTo(myPoint.x, myPoint.y);
  3.   for (var i:uint = 0; i < nLength; i++) {
  4.     myPoint = vertices2D[i];
  5.     myGraphics.lineTo(myPoint.x, myPoint.y);
  6.   }
  7. }

まず、関数xGetVertices2D()は、3次元空間座標のVector3Dがベース型のVectorオブジェクトを引数に受取り、xy座標がPointエレメントに納められたVectorオブジェクトを返します(スクリプト第28〜36行目)。

スクリプト第29行目は、戻り値にするPointインスタンスを生成します。そして、第30〜34行目のforループの処理で、引数のVectorインスタンスから順に取出したVector3Dオブジェクトのxy座標をPointオブジェクトに設定して、戻り値のVectorオブジェクトに加えているだけです。第25行目は、でき上がったVectorオブジェクトを返しています。

つぎに、関数xDrawLines()は引数のVectorインスタンスからPointエレメントのxy座標を順に取出して、Graphicsクラスのメソッドによりワイヤーフレームを描きます(スクリプト第37〜47行目)。

スクリプト第39行目は、Vectorインスタンスの最後のエレメントのインデックスを調べています。これは閉じた形状を描くため、第42行目で描画の始まりを最後のPointエレメントの座標にするからです。こうすると、第43〜46行目のforループで、Vectorインスタンスのインデックス0から最後まで、Pointオブジェクトの座標にしたがって単純に直線を引けばよいことになります。

ワイヤーフレームを回すためにもうひとつ知らなければならないのは、Vector3Dオブジェクトの座標をどうやって回転するかです。Vector3Dクラスには、そのようなメソッドは備わっていません。Vector3Dオブジェクトの座標変換には、Matrix3Dクラスを使います。

Matrix3D.transformVector()メソッドを用いると、引数のVector3Dオブジェクトに変換行列が適用されます(シンタックス06-003)。したがって、Matrix3Dインスタンスに平行移動や回転、あるいは伸縮といった変換を加えたうえで、引数としたVector3Dオブジェクトに対してMatrix3D.transformVector()メソッドを呼出せばよいのです。

シンタックス06-003■Matrix3D.transformVector()メソッド
Matrix3D.transformVector()メソッド
文法 transformVector(targetVector3D:Vector3D):Vector3D
概要 Matrix3Dオブジェクトの変換行列を用いて、Vector3Dインスタンスの座標を変換し、新たなVector3Dインスタンスとして返す。
引数 targetVector3D:Vector3D ― 座標を変換する対象のVector3Dインスタンス。
戻り値 座標変換された新たなVector3Dインスタンス。

これで回す用意は整いました。でき上がったフレームアクションは、以下のスクリプト06-001のとおりです。座標変換の関数はxTransform()として定義します。引数には変換するVector3Dエレメントが納められたVectorインスタンスと、水平回転の角度を渡します。

DisplayObject.enterFrameイベント(定数Event.ENTER_FRAME)のリスナー関数xRotate()は、3つの関数を呼出します(スクリプト第14〜19行目)。第1に、マウスポインタの水平座標に応じた回転角を計算したうえで、関数xTransform()でVectorインスタンス内のVector3Dエレメントの3次元座標を回転します。第2に、xGetVertices2D()により、2次元座標のPointエレメントが納められたVectorインスタンスを得ています。そのうえで第3に、引数として渡したそのVectorインスタンスにもとづいて、xDrawLines()がワイヤーフレームを描きます。なお、アニメーションは毎フレーム描き直す必要がありますので、スクリプト第40行目でGraphics.clear()メソッド(シンタックス06-002)を呼出しています。

スクリプト06-001■Vector3Dオブジェクトで座標が定められた正方形のワイヤーフレームを回す
    // フレームアクション
  1. var nUnit:Number = 100 / 2;
  2. var nDeceleration:Number = 0.3;
  3. var mySprite:Sprite = new Sprite();
  4. var myGraphics:Graphics = mySprite.graphics;
  5. var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
  6. addChild(mySprite);
  7. mySprite.x = stage.stageWidth / 2;
  8. mySprite.y = stage.stageHeight / 2;
  9. vertices.push(new Vector3D(-nUnit, -nUnit, 0));
  10. vertices.push(new Vector3D(nUnit, -nUnit, 0));
  11. vertices.push(new Vector3D(nUnit, nUnit, 0));
  12. vertices.push(new Vector3D(-nUnit, nUnit, 0));
  13. addEventListener(Event.ENTER_FRAME, xRotate);
  14. function xRotate(eventObject:Event):void {
  15.   var nRotationY:Number = mySprite.mouseX * nDeceleration;
  16.   xTransform(vertices, nRotationY);
  17.   var vertices2D:Vector.<Point> = xGetVertices2D(vertices);
  18.   xDrawLines(vertices2D);
  19. }
  20. function xTransform(myVertices:Vector.<Vector3D>, myRotation:Number):void {
  21.   var nLength:uint = myVertices.length;
  22.   var myMatrix3D:Matrix3D = new Matrix3D();
  23.   myMatrix3D.appendRotation(myRotation, Vector3D.Y_AXIS);
  24.   for (var i:int = 0; i<nLength; i++) {
  25.     myVertices[i] = myMatrix3D.transformVector(myVertices[i]);
  26.   }
  27. }
  28. function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point> {
  29.   var vertices2D:Vector.<Point> = new Vector.<Point>();
  30.   var nLength:uint = myVertices.length;
  31.   for (var i:uint = 0; i < nLength; i++) {
  32.     var myVector3D:Vector3D = myVertices[i];
  33.     vertices2D.push(new Point(myVector3D.x, myVector3D.y));
  34.   }
  35.   return vertices2D;
  36. }
  37. function xDrawLines(vertices2D:Vector.<Point>):void {
  38.   var nLength:uint = vertices2D.length;
  39.   var myPoint:Point = vertices2D[nLength - 1];
  40.   myGraphics.clear();
  41.   myGraphics.lineStyle(2, 0);
  42.   myGraphics.moveTo(myPoint.x, myPoint.y);
  43.   for (var i:uint = 0; i < nLength; i++) {
  44.     myPoint = vertices2D[i];
  45.     myGraphics.lineTo(myPoint.x, myPoint.y);
  46.   }
  47. }

関数xTransform()は、Matrix3D.transformVector()メソッドさえおわかりになれば、簡単でしょう(スクリプト第20〜27行目)。第22〜23行目は、新たなMatrixインスタンスを生成し、Matrix3D.appendRotation()メソッドで回転を加えます。そして、第24〜26行目のforループでVectorインスタンスからエレメントのVector3Dオブジェクトを順に取出して、Matrix3D.transformVector()メソッドで変換しています。

ただし、Matrix3D.transformVector()メソッドは引数のVector3Dオブジェクトそのものは書替えません。変換された新たなVector3Dインスタンスがメソッドから返されますので、そのオブジェクトを第25行目でVectorエレメントに上書きしています。

[ムービープレビュー]を見ると、マウスポインタの水平位置に合わせて、ワイヤーフレームの四角形が回ります。もっとも、その動きには不満が残ります。すでに予想されていた読者も、いらっしゃるでしょう。四角形は回転というより、ただ左右に伸び縮みしているだけです(図06-005)。Vector3Dオブジェクトの3次元座標から単純にxy座標の値を取出して、矩形が描かれているからです。いわゆるパースペクティブがかかっていません。

図06-005■四角形のワイヤーフレームが左右に伸び縮みするだけ


Vector3Dオブジェクトの3次元座標から単純にxy座標の値を取出して、矩形が描かれているため、パースペクティブがかからない。

○06-02 遠近法が投影されたワイヤーフレームの立方体を回す
3次元空間の座標を2次元平面のスクリーンに引き移す遠近法投影もしくは透視投影については、前述02「遠近法の投影 − PerspectiveProjectionクラス」で解説しました。その02-05「焦点距離の操作 − PerspectiveProjection.focalLengthプロパティ」で示したのが再掲図02-013です。

図02-013■z軸における焦点距離と視野角(再掲)
焦点距離が長いと、視野角は狭く、オブジェクトの投影像は大きく表示される。逆に、焦点距離が短ければ、視野角は広がり、投影像は小さく見える。

図のもとのオブジェクトと投影像をそれぞれ底辺とし、ともに視点が頂点となる相似なふたつの三角形から、比率がつぎのように求められます(Tips 02-004「焦点距離と遠近法投影(透視投影)の比率」)。

投影像の大きさ/オブジェクトの大きさ = 焦点距離 / (焦点距離 + z位置)
投影像の大きさ = オブジェクトの大きさ×焦点距離 / (焦点距離 + z位置)

したがって、3次元空間のz座標値に応じてxy座標値を2次元平面に遠近法投影(透視投影)する比率はつぎのとおりです。

焦点距離 / (焦点距離 + z位置)

よって、前掲スクリプト06-001の関数xTransform()で、Vector3Dオブジェクトの3次元座標から単純にxy座標の値を取出すだけではなく、この遠近法投影の比率を掛合わせればよいのです。早速、この処理を加えてみましょう。ただその前に、シンタックス06-001のVector3D.wプロパティの説明を、もう1度読み直してください。

ただし、Vector3D.wプロパティは3次元座標とは別のオプションとして用いられる。透視投影比率を設定すると、Vector3D.project()メソッドによりxyz座標値を除する値となる。

この気になるメソッドVector3D.project()の説明は、シンタックス06-004のとおりです。透視投影の比率をVector3D.wプロパティに設定しておけば、Vector3D.project()メソッドが変換の計算はやってくれます。

シンタックス06-004■Vector3D.project()とVector3D.clone()メソッド
Vector3D.project()メソッド
文法 project():void
概要 Vector3DインスタンスのVector3D.x/y/zの各座標値をVector3D.wプロパティの値で除する。3次元空間から2次元平面への座標の透視投影変換などに用いられる。
引数 なし。
戻り値 なし。
Vector3D.clone()メソッド
文法 clone():void
概要 Vector3Dインスタンスを複製して、新たなオブジェクトとして返す。
引数 なし。
戻り値 なし。

Vector3D.project()メソッドを使うにあたって、注意することはふたつあります。第1は、xyz各座標値はVector3D.wプロパティの値で割り算されます。したがって、このプロパティに設定するのは、つぎのような前述の比率の逆数にしなければなりません。

(焦点距離 + z位置) / 焦点距離

第2に、Vector3D.project()メソッドは、参照したVector3Dインスタンスの座標値そのものを書替えます。ですから、3次元空間の座標値を保っておくには、オブジェクトを複製する必要があります。そのためのメソッドが、前掲シンタックス06-004のVector3D.clone()です。

そこで、前掲スクリプト06-001を修正します。Vector3D.wプロパティとVector3D.project()メソッドを用いて遠近法投影(透視投影)するように書替えたのが、つぎのフレームアクションです(スクリプト06-002)。

スクリプト06-002■Vector3Dオブジェクトで座標が定められた正方形のワイヤーフレームを透視投影して回す
    // フレームアクション
  1. var nUnit:Number = 100 / 2;
  2. var nDeceleration:Number = 0.3;
  3. var mySprite:Sprite = new Sprite();
  4. var myGraphics:Graphics = mySprite.graphics;
  5. var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
  6. var nFocalLength:Number = nUnit * 10;
  7. addChild(mySprite);
  8. mySprite.x = stage.stageWidth / 2;
  9. mySprite.y = stage.stageHeight / 2;
  10. vertices.push(new Vector3D(-nUnit, -nUnit, 0));
  11. vertices.push(new Vector3D(nUnit, -nUnit, 0));
  12. vertices.push(new Vector3D(nUnit, nUnit, 0));
  13. vertices.push(new Vector3D(-nUnit, nUnit, 0));
  14. addEventListener(Event.ENTER_FRAME, xRotate);
  15. function xRotate(eventObject:Event):void {
  16.   var nRotationY:Number = mySprite.mouseX * nDeceleration;
  17.   xTransform(vertices, nRotationY);
  18.   var vertices2D:Vector.<Point> = xGetVertices2D(vertices);
  19.   xDrawLines(vertices2D);
  20. }
  21. function xTransform(myVertices:Vector.<Vector3D>, myRotation:Number):void {
  22.   var nLength:uint = myVertices.length;
  23.   var myMatrix3D:Matrix3D = new Matrix3D();
  24.   myMatrix3D.appendRotation(myRotation, Vector3D.Y_AXIS);
  25.   for (var i:int = 0; i<nLength; i++) {
  26.     myVertices[i] = myMatrix3D.transformVector(myVertices[i]);
  27.   }
  28. }
  29. function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point> {
  30.   var vertices2D:Vector.<Point> = new Vector.<Point>();
  31.   var nLength:uint = myVertices.length;
  32.   for (var i:uint = 0; i < nLength; i++) {
  33.     var myVector3D:Vector3D = myVertices[i].clone();
  34.     myVector3D.w = (nFocalLength + myVector3D.z) / nFocalLength;
  35.     myVector3D.project();
  36.     vertices2D.push(new Point(myVector3D.x, myVector3D.y));
  37.   }
  38.   return vertices2D;
  39. }
  40. function xDrawLines(vertices2D:Vector.<Point>):void {
  41.   var nLength:uint = vertices2D.length;
  42.   var myPoint:Point = vertices2D[nLength - 1];
  43.   myGraphics.clear();
  44.   myGraphics.lineStyle(2, 0);
  45.   myGraphics.moveTo(myPoint.x, myPoint.y);
  46.   for (var i:uint = 0; i < nLength; i++) {
  47.     myPoint = vertices2D[i];
  48.     myGraphics.lineTo(myPoint.x, myPoint.y);
  49.   }
  50. }

まず、スクリプト第6行目で、焦点距離の変数(nFocalLength)を設定しました。つぎに、関数xGetVertices2D()に透視投影の処理を加えています。forループ(第31〜37行目)の中で、第33行目は透視投影のために、Vector3DオブジェクトをVector3D.clone()で複製します。そして第34行目で、その複製したオブジェクトのVector3D.wプロパティに、前記の透視投影比率を設定します。そのうえで第35行目は、Vector3D.project()メソッドを呼出して透視投影します。

これで[ムービープレビュー]を確かめると、今度は遠近法の投影されたワイヤーフレームの動きに変わっています(図06-006)。

図06-006■四角形のワイヤーフレームが透視投影されて回る


Vector3Dオブジェクトの3次元座標を透視投影したうえで、ワイヤーフレームが描かれている。

ここまでできたら、つぎにお約束としてやりたくなるのは立方体を回すことです。幸いワイヤーフレームは、重ね順を考えなくて済みます。3次元空間に関わる知識として、新たに覚えるべきことはありません。けれども、数多くのデータ(座標値)を扱うことは、3次元空間の処理にありがちです。その練習問題として、考えてみましょう。

立方体の8頂点の座標値は、原点(0, 0, 0)を中心にして下図06-007のように定めます。前掲スクリプト06-002と同じ正方形をふたつ(頂点番号0-1-2-3と4-5-6-7)、z座標を(変数nUnitの値だけ)前後させて向合わせたかたちです。

図06-007■3次元空間に立方体の座標を定める
原点(0, 0, 0)が中心になるように、立方体の8頂点の座標を決める。

取りあえず、前掲スクリプト06-002の3次元座標値を、上図06-007の頂点0〜7の8つの座標値に差替えてみましょう。つまり、スクリプト06-002の第10〜13行目を、つぎのように書替えます。

vertices.push(new Vector3D(-nUnit, -nUnit, -nUnit));
vertices.push(new Vector3D(nUnit, -nUnit, -nUnit));
vertices.push(new Vector3D(nUnit, nUnit, -nUnit));
vertices.push(new Vector3D(-nUnit, nUnit, -nUnit));
vertices.push(new Vector3D(-nUnit, -nUnit, nUnit));
vertices.push(new Vector3D(nUnit, -nUnit, nUnit));
vertices.push(new Vector3D(nUnit, nUnit, nUnit));
vertices.push(new Vector3D(-nUnit, nUnit, nUnit));

[ムービープレビュー]を見ると、マウスポインタの水平位置にしたがって立方体の頂点が回ります。座標の回転も、遠近法の投影も、正しく行われています。ただし、単純に8頂点の座標を放り込んだため、前面と後面の正方形がたすき掛けのようにつながってしまうのです(図06-008)。

図06-008■ふたつの面の正方形がたすき掛けのようにつながる
単純に8頂点の座標を放り込んだため、すべての座標がひと筆書きで描かれる。

問題はスクリプト06-002のワイヤーフレームを描く処理、具体的には関数xDrawLines()だということなります。この関数は、与えられた頂点をひと筆書きのように線で結びます。しかし、立方体はひと筆書きでは描けません。もっとも逆にいえば、ひと筆書きにしなければ立方体のワイヤーフレームもできます。つまり、頂点座標を重複して加え、ひとつの辺を何度か上書きすればよいのです。

Maniac! 06-002■ひと筆書きできる図形
立方体の各頂点は、3つの辺を結ぶ三叉路です。ひと筆書きで三叉路は、最終的に出たら戻ることはできず、到達したら出られません。つまり、出発点か到達点かのどちらかにする必要があります。しかし、出発点と到達点はひとつずつしか決められませんから、三叉路が3つ以上あったらひと筆書きはできないということになります。つまり、8頂点が三叉路の立方体は、ひと筆書きできません。

一般的に、奇数の頂点や交点がないか、またはそれをふたつもつ図形だけがひと筆書きできます。なお、奇数の頂点・交点を「奇数点」と呼びます。

けれども、数多くのデータを扱う処理としてはいただけません。とくに、無駄な描画はできるかぎり省きたいです。そこで、もうひとつVectorインスタンスを用意します。そのインスタンスには、ワイヤーフレームで結ぶ頂点番号の組を納めます。つまり、正方形の前面(頂点番号0-1-2-3)と後面(同4-5-6-7)、そして互いの4つの頂点を結ぶ線(同0-4、1-5、2-6、3-7)がエレメントになります。さらに、このVectorエレメントは整数の組です。そこで、これはベース型uintのVectorオブジェクトにします。つまり、Vectorインスタンスの入れ子になるということです。

後に掲げるでき上がりのスクリプト06-003では、この頂点番号の組を納めたVectorインスタンスをつぎのように作成しました。エレメントとなる入れ子のベース型uintのVectorオブジェクトは、整数の配列をVector()関数で変換しています(前掲シンタックス05-003)。

  1. var indices:Vector.<Vector.<uint>> = new Vector.<Vector.<uint>>();
  1. indices.push(Vector.<uint>([0, 1, 2, 3]));
  2. indices.push(Vector.<uint>([4, 5, 6, 7]));
  3. indices.push(Vector.<uint>([0, 4]));
  4. indices.push(Vector.<uint>([1, 5]));
  5. indices.push(Vector.<uint>([2, 6]));
  6. indices.push(Vector.<uint>([3, 7]));

さて、立方体を描くには、関数xDrawLines()が問題だといいました。けれど、スクリプト06-003では、この関数の基本的な処理は変えていません(スクリプト第65〜70行目)。Vectorインスタンスから2次元座標のPointエレメントを取出して線描する、という基本的な機能は引続き必要だからです。

その代わり、新たにxDraw()関数を定義して、前処理を委ねます(スクリプト第52〜64行目)。つまり、8頂点のxy座標値と頂点番号の組のふたつのVectorオブジェクトから、頂点の組ごとのxy座標値が納められたベース型PointのVectorオブジェクトをつくり、ワイヤーフレームは関数xDrawLines()に描かせる訳です。

ひとつの関数に処理をすべて詰込むのではなく、比較的単純な機能の関数を組合わせることには大きくふたつの利点があります。第1に、うまくデザインすれば、単純な処理の方が部品として組合わせやすく、流用しやすいということです。第2に、バグをつぶしたり、細かな調整・改善をするときも、処理内容は単純な方が簡単です。

[イラスト] 関数は単純な機能を組合わせた方が、応用しやすくメンテナンスも簡単。

スクリプト06-003■Vector3Dオブジェクトで座標が定められた立方体のワイヤーフレームを透視投影して回す
    // フレームアクション
  1. var nUnit:Number = 100 / 2;
  2. var nDeceleration:Number = 0.3;
  3. var mySprite:Sprite = new Sprite();
  4. var myGraphics:Graphics = mySprite.graphics;
  5. var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
  6. var indices:Vector.<Vector.<uint>> = new Vector.<Vector.<uint>>();
  7. var nFocalLength:Number = nUnit * 10;
  8. addChild(mySprite);
  9. mySprite.x = stage.stageWidth / 2;
  10. mySprite.y = stage.stageHeight / 2;
  11. vertices.push(new Vector3D(-nUnit, -nUnit, -nUnit));
  12. vertices.push(new Vector3D(nUnit, -nUnit, -nUnit));
  13. vertices.push(new Vector3D(nUnit, nUnit, -nUnit));
  14. vertices.push(new Vector3D(-nUnit, nUnit, -nUnit));
  15. vertices.push(new Vector3D(-nUnit, -nUnit, nUnit));
  16. vertices.push(new Vector3D(nUnit, -nUnit, nUnit));
  17. vertices.push(new Vector3D(nUnit, nUnit, nUnit));
  18. vertices.push(new Vector3D(-nUnit, nUnit, nUnit));
  19. indices.push(Vector.<uint>([0, 1, 2, 3]));
  20. indices.push(Vector.<uint>([4, 5, 6, 7]));
  21. indices.push(Vector.<uint>([0, 4]));
  22. indices.push(Vector.<uint>([1, 5]));
  23. indices.push(Vector.<uint>([2, 6]));
  24. indices.push(Vector.<uint>([3, 7]));
  25. addEventListener(Event.ENTER_FRAME, xRotate);
  26. function xRotate(eventObject:Event):void {
  27.   var myRotation:Point = new Point(mySprite.mouseX * nDeceleration, mySprite.mouseY * nDeceleration);
  28.   xTransform(vertices, myRotation);
  29.   var vertices2D:Vector.<Point> = xGetVertices2D(vertices);
  30.   xDraw(vertices2D, indices);
  31. }
  32. function xTransform(myVertices:Vector.<Vector3D>, myRotation:Point):void {
  33.   var nLength:uint = myVertices.length;
  34.   var myMatrix3D:Matrix3D = new Matrix3D();
  35.   myMatrix3D.appendRotation(myRotation.x, Vector3D.Y_AXIS);
  36.   myMatrix3D.appendRotation(myRotation.y, Vector3D.X_AXIS);
  37.   for (var i:int = 0; i<nLength; i++) {
  38.     myVertices[i] = myMatrix3D.transformVector(myVertices[i]);
  39.   }
  40. }
  41. function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point> {
  42.   var vertices2D:Vector.<Point> = new Vector.<Point>();
  43.   var nLength:uint = myVertices.length;
  44.   for (var i:uint = 0; i < nLength; i++) {
  45.     var myVector3D:Vector3D = myVertices[i].clone();
  46.     myVector3D.w = (nFocalLength + myVector3D.z) / nFocalLength;
  47.     myVector3D.project();
  48.     vertices2D.push(new Point(myVector3D.x, myVector3D.y));
  49.   }
  50.   return vertices2D;
  51. }
  52. function xDraw(vertices2D:Vector.<Point>, myIndices:Vector.<Vector.<uint>>):void {
  53.   var nLength:uint = myIndices.length;
  54.   myGraphics.clear();
  55.   for (var i:uint = 0; i < nLength; i++) {
  56.     var myVertices:Vector.<Point> = new Vector.<Point>();
  57.     var myIndex:Vector.<uint> = myIndices[i];
  58.     var nLength2:uint = myIndex.length;
  59.     for (var j:uint = 0; j < nLength2; j++) {
  60.       myVertices.push(vertices2D[myIndex[j]]);
  61.     }
  62.     xDrawLines(myVertices);
  63.   }
  64. }
  65. function xDrawLines(vertices2D:Vector.<Point>):void {
  66.   var nLength:uint = vertices2D.length;
  67.   var myPoint:Point = vertices2D[nLength - 1];
  68.   if (nLength < 3) {
  69.     --nLength;
  70.   }
  71.   myGraphics.lineStyle(2, 0);
  72.   myGraphics.moveTo(myPoint.x, myPoint.y);
  73.   for (var i:uint = 0; i < nLength; i++) {
  74.     myPoint = vertices2D[i];
  75.     myGraphics.lineTo(myPoint.x, myPoint.y);
  76.   }
  77. }

DisplayObject.enterFrameイベント(定数Event.ENTER_FRAME)のリスナー関数xRotate()からは、スクリプト第30行目で新たな関数xDraw()を呼出すことにしました。引数はふたつのVectorオブジェクトで、ベース型をそれぞれPointとVectorとし、透視投影した8頂点のxy座標値(ローカル変数vertices2D)とワイヤーフレームを描く頂点の組(変数indices)が各インスタンスに納められています。

なお、立方体は垂直方向にも回すことにします。そのため、関数xRotate()の第27〜28行目は、マウスポインタの垂直方向の位置も調べてxy座標をPointインスタンスとし、関数xTransform()の呼出しでそのPointインスタンスを第2引数に渡しています。また、関数xTransform()(第22〜40行目)は引数として受取ったPointインスタンスの座標値にもとづき、第36行目でMatrix3D.appendRotation()による垂直方向の回転を加えました。

スクリプト第52〜64行目に定義された関数xDraw()は、第54行目でSpriteインスタンスのワイヤーフレームを消します。正方形を描画した前掲スクリプト06-002では、この処理は関数xDrawLines()にありました。しかし、このスクリプト06-003は関数xDrawLines()を各パーツの描画に用いますので、その度に他のパーツを消しては困ります。そこで、関数xDraw()にステートメントを移しました。

第55行目からのforステートメントは、第56行目で関数xDrawLines()に渡すベース型PointのVectorインスタンス(変数myVertices)を生成したうえで、関数xDraw()が第2引数として受取ったVectorインスタンスから頂点番号の組のVectorエレメントを順に取出します。そして、第59〜61行目の入れ子のforループが、頂点番号に対応したxy座標値のPointオブジェクトを第1引数のVectorインスタンスから得て、第56行目でつくったVectorインスタンス(変数myVertices)に加えます。

2重forループの最後の処理は、関数xDrawLines()の呼出しです(第62行目)。引数は、関数xDrawLines()に頂点番号の組に合ったPointエレメントが納められたVectorインスタンス(変数myVertices)です。これで、頂点番号の組ごとに、ワイヤーフレームが描かれることになります。

関数xDrawLines()(第65〜77行目)は、Spriteインスタンスの描画の消去をxDraw()(第54行目)に移したほかに、もうひとつだけ手を加えました。第68〜70行目のifステートメントです。この関数は、もともと閉じた図形を描く設計でした。しかし、ふたつの正方形の4頂点を結ぶ各辺は、閉じていません。もとのままでは、閉じるために線を往復して描きます。

もっとも、見た目には問題は生じません。けれども、前述のとおり描画の無駄はできるだけ省きます。そこで、頂点がふたつしかない1本の線、つまり頂点の組のVectorエレメント数(Vector.lengthプロパティ)が3より小さいときには、最後の頂点座標に戻って閉じる線を引かないように、forループの条件に指定する処理の総数(変数nLength)をひとつ減らしています。

[ムービープレビュー]を確かめると、マウスポインタの位置に応じて立方体のワイヤーフレームが上下左右に回ります(図06-009左図)。ちなみに、ワイヤーフレームで線の前後関係を錯覚すると、立方体がゆがんで逆に回っているように見えるのでご注意ください(図06-009右図は一番手前の垂直の辺を隠してみました)。

図06-009■ふたつの正方形と各4頂点を結んで立方体のワイヤーフレームが描かれる
頂点番号の組にしたがって、ふたつの正方形と4つの頂点をそれぞれ結んで、立方体のワイヤーフレームができる(左図)。手前の辺が奥にあるように錯覚すると、立方体がゆがんで逆に回っているように見える(右図は一番手前の垂直の辺を隠した)。

○06-03 面が表向きか裏向きかを調べる − ベクトルの外積と内積
Vector3Dクラスのメソッドを使うと、面の向きが裏か表かを調べることができます。まず、面の向きはVector3D.crossProduct()メソッドで得られるベクトルの外積を表すVector3Dオブジェクトから求められます。その面の向きと視線を表すVector3Dインスタンスとのベクトルの内積の値により、面の視線に対する向きがわかります。内積を導くメソッドは、Vector3D.dotProduct()です。

シンタックス06-005には、Vector3D.crossProduct()とVector3D.dotProduct()メソッドのほか、加減算のVector3D.add()やVector3D.subtract()メソッド、それにVector3Dオブジェクトの表すベクトルの長さを単位ベクトルにするVector3D.normalize()メソッドが掲げてあります。

シンタックス06-005■Vector3Dクラスの面の向きを調べるためのプロパティとメソッド
Vector3D.lengthプロパティ
文法 length:Number
プロパティ値 [読取り専用] Vector3Dインスタンスの表す3次元座標ベクトル(x, y, z)の長さ(大きさ)。なお、ベクトルAの長さは、絶対値の記号を用いて「|A|」で示される。。
Vector3D.add()メソッド
文法 add(secondVector:Vector3D):Vector3D
概要 参照するVector3Dインスタンスに引数のVector3Dインスタンスがベクトル演算として加算された結果を、新たなVector3Dオブジェクトで返す。
引数 secondVector:Vector3D ― 加算するベクトルを示すVector3Dインスタンス。
戻り値

加算の結果となるベクトルを示す新たなVector3Dインスタンス(図06-010)。xyz各座標ごとに、ふたつのベクトルの値が足し算される。

図06-010■ベクトルの幾何学的な加算
→
足し算は、ふたつのベクトルをつなげて、始点と終点を結ぶ。
Vector3D.subtract()メソッド
文法 subtract(secondVector:Vector3D):Vector3D
概要 参照するVector3Dインスタンスから引数のVector3Dインスタンスがベクトル演算として減算された結果を、新たなVector3Dオブジェクトで返す。
引数 secondVector:Vector3D ― 減算するベクトルを示すVector3Dインスタンス。
戻り値

減算の結果となるベクトルを示す新たなVector3Dインスタンス(図06-011)。xyz各座標ごとに、ふたつのベクトルの値が引き算される。

図06-011■ベクトルの幾何学的な減算
→
引き算は、引くベクトルの方向を反転して加算する。
Vector3D.crossProduct()メソッド
文法 crossProduct(secondVector:Vector3D):Vector3D
概要 参照するVector3Dインスタンスと引数のVector3Dインスタンスのベクトル演算としての外積を、新たなVector3Dオブジェクトで返す。戻り値のVector3Dオブジェクトは、参照したVector3Dインスタンスと引数に渡したもうひとつのVector3Dインスタンスの両方に垂直なベクトルを表す。
引数 secondVector:Vector3D ― 外積を計算するためのもうひとつのベクトルとなるVector3Dインスタンス。
戻り値

外積として計算されたベクトルを示す新たなVector3Dインスタンス。ふたつのベクトルAとBとの外積は、「A×B」で表される(表06-002参照)。参照したVector3Dインスタンスとメソッドの引数に渡したもうひとつのVector3Dインスタンスとが互いに平行な場合、外積としてベクトル(0, 0, 0)のVector3Dインスタンスが返される。

表06-002■外積で求められるベクトル
外積の要素 求められた外積のベクトルとふたつのベクトルの関係
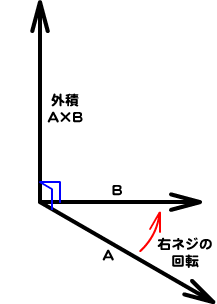
角度 ふたつのベクトルAとBを含む平面に垂直。
方向 ベクトルAからBに向かう回転を考えたとき、その回し方で右ネジの進む方向。
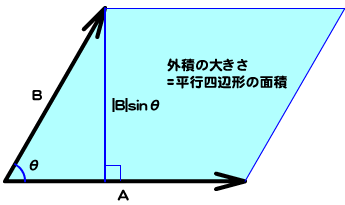
大きさ ベクトルAからBを平行四辺形の隣り合う2辺としたとき、ベクトルの外積の大きさ|A×B|はこの平行四辺形の面積|A||B|sinθと等しい。
Vector3D.dotProduct()メソッド
文法 dotProduct(secondVector:Vector3D):Number
概要 参照するVector3Dインスタンスと引数のVector3Dインスタンスのベクトル演算としての内積を数値で返す。戻り値から、参照したVector3Dインスタンスと引数に渡したもうひとつのVector3Dインスタンスが表すふたつのベクトルのなす角が調べられる。
引数 secondVector:Vector3D ― 内積を計算するためのもうひとつのベクトルとなるVector3Dインスタンス。
戻り値

内積として計算された数値。ふたつのベクトルAとBとの内積は、つぎの式で表される(表06-003参照)。

A・B = |A||B|cosθ

参照したVector3Dインスタンスとメソッドの引数に渡したもうひとつのVector3Dインスタンスとが互いに垂直な場合、内積として0が返される。

表06-003■ベクトルの内積となす角
内積の値 なす角(θ) cosθ
正 90度より小さい(鋭角) 正
0 90度(直角) 0
負 90度より大きい(鈍角) 負
Vector3D.normalize()メソッド
文法 normalize():Number
概要 参照するVector3Dインスタンスの方向は変えずに、長さ(Vector3D.lengthプロパティ値)1の単位ベクトルにする。Vector3D.wプロパティの値は変わらない。インスタンスの表すベクトルのxyz各座標値は、長さの値で除算される。
引数 なし。
戻り値 参照したもとのVector3Dインスタンスのベクトルの長さ(Vector3D.lengthプロパティ値)。

[*筆者用参考]「Vector3D.crossProduct()メソッド」、「Vector3D.dotProduct()メソッド」、「ベクトルの内積や外積で3次元空間における面の向きを知りたい」。

Maniac! 06-003■[ヘルプ]のVector3D.crossProduct()メソッドの説明
[ヘルプ]で[Vector3D]クラスの「crossProduct()メソッド」の項を読むと、戻り値について本稿執筆時点ではつぎのように説明されています。

返されたVector3Dオブジェクトの座標が(0, 0, 0)の場合、2つのVector3Dオブジェクトは互いに垂直です。

しかし、このときふたつのVector3Dオブジェクトが表すベクトルは、互いに「垂直」ではなく「平行」です。前掲シンタックス06-005のVector3D.crossProduct()メソッドで解説したとおり、ベクトルAとBとの外積の大きさは|A||B|sinθです(解説中の表06-002)。したがって、ふたつのベクトルのなす角θが0つまり平行なとき、sinθは0ですので、外積を表すベクトルの大きさ(長さ)も0になります。

Vector3D.crossProduct()メソッドにより、ふたつの3次元座標ベクトルを表すVector3Dインスタンスから、その両方に対して垂直なベクトルのVector3Dオブジェクトが求められます。このベクトル演算を「外積」と呼びます。

平面の向きは、その面に対して垂直なベクトルで定義されます。平面上の(平行でない)ふたつのベクトルから外積を求めれば、それは面に対して垂直なベクトルになります。つまり、面の向きが決まるのです。

たとえば、面の頂点を結んだふたつのVector3DインスタンスmyVectorとsecondVectorがあるとき、つぎのように呼出したVector3D.crossProduct()メソッドから得られるVector3DオブジェクトcrossProductVectorは、面に対して垂直なベクトルになります(図06-012)。

var crossProductVector:Vector3D = myVector.crossProduct(secondVector);
図06-012■面の頂点を結ぶ2ベクトルからVector3D.crossProduct()メソッドで垂直ベクトルが得られる
参照するベクトルから引数のベクトルの位置は、右ネジの回転方向になっている必要がある。

ただし、面に垂直なベクトルは、面に対して前後の2方向考えられます。そのため、Vector3D.crossProduct()メソッドで参照するVector3Dインスタンスと引数のVector3Dインスタンスの順序が大切です。参照するベクトルから引数のベクトルの位置が右ネジの回転になるように、垂直ベクトルの方向は定められます(上図06-012)。

面の向きが決まると、それが視線に対して表か裏かは、Vector3D.dotProduct()メソッドで求められます。このメソッドは、ふたつのベクトルの「内積」を計算します。

外積からはベクトルが得られたのに対して、内積は(実)数値になります。ふたつのベクトルが互いに垂直なとき値は0です。鋭角ではプラスで、鈍角のときマイナスになります(前掲シンタックス06-005表06-003)。

なお、内積ではふたつのベクトルの計算順序は、結果に関わりません。ですから、Vector3D.dotProduct()メソッドでどちらのベクトルのVector3Dインスタンスを参照して、どちらを引数にしても、戻り値は同じです。

ベクトルの外積と内積の数学的な意味やその計算については、数学編で解説します。

[イラスト] 面の向きは外積で求めて、裏か表かは内積で調べる。

Maniac! 06-004■外積と内積の別名
外積と内積は、それぞれ「クロス積」と「ドット積」とも呼ばれます。掛合わせた数を意味する「積」は、英語で"product"です。つまり、この呼び名がVector3Dクラスのメソッド名Vector3D.crossProduct()とVector3D.dotProduct()に用いられました。なお、クロスやドットは、外積と内積を表す演算記号「×」(クロス)と「・」(ドット)に由来します。

[*筆者用参考]「内積と外積」

それでは練習問題として、平面の頂点座標から、その面が視線に対して裏か表か調べる関数を定義してみましょう。平面の頂点座標はVector3Dオブジェクトにして、Vectorインスタンスに納めることにします。

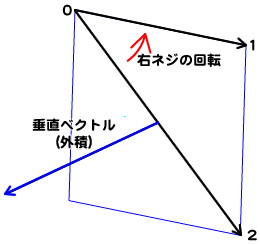
頂点座標は、ふたつのベクトルを求めるためには、3つ必要になります。しかも、外積から垂直ベクトルの方向が決まるように、頂点の順番も定めておかなければなりません。ここでは、前掲スクリプト06-001と同じように、頂点を時計回りに指定します。すると、頂点0から2のベクトルと頂点0から1のベクトルとの外積を求めることにより、平面の向きとなるベクトルが決まります(図06-013)。

図06-013■平面の頂点番号を時計回りに定める
頂点0から2のベクトルと頂点0から1のベクトルとの外積を求めることにより、平面の向きとなる垂直ベクトルが決まる。

ふたつの位置座標BからAを結ぶベクトルは、位置ベクトルAからBを引き算することにより求められます。用いるメソッドはVector3D.subtract()です(前掲シンタックス06-005)。ベクトルAのVector3Dインスタンスを参照して、引くベクトルBのVector3Dインスタンスを引数に渡します。

以下のスクリプト06-004に定義された関数xIsFrontは、平面の頂点座標のVector3Dエレメントを納めたVectorインスタンスと視線のVector3Dオブジェクトのふたつの引数が渡されると、その面が視線に対して裏か表かをブール(論理)値で返します。

スクリプト06-004■平面の頂点座標から視線に対する裏表の向きを返す関数
    // フレームアクション
  1. function xIsFront(myVertices:Vector.<Vector3D>, myView:Vector3D):Boolean {
  2.   var vector3D_0:Vector3D = myVertices[0];
  3.   var vector3D_1:Vector3D = myVertices[1];
  4.   var vector3D_2:Vector3D = myVertices[2];
  5.   var vector3D_0_1:Vector3D = vector3D_1.subtract(vector3D_0);
  6.   var vector3D_0_2:Vector3D = vector3D_2.subtract(vector3D_0);
  7.   var direction3D:Vector3D = vector3D_0_2.crossProduct(vector3D_0_1);
  8.   direction3D.normalize();
  9.   var bFront:Boolean = (direction3D.dotProduct(myView) < 0);
  10.   return bFront;
  11. }

スクリプト第2〜4行目は、Vectorインスタンスから頂点(インデックス)番号0〜2の3つの座標のVector3Dエレメントを取出します。そして、第5〜6行目で、Vector3D.subtract()メソッドにより、頂点0から1(変数vector3D_0_1)と2(変数vector3D_0_2)のふたつのベクトルのVector3Dオブジェクトを得ています。

スクリプト第7行目は、右ネジの方向に頂点0から2と1のふたつのベクトルから、Vector3D.crossProduct()で面の方向となる垂線のベクトル(変数direction3D)を求めます(前掲図06-013参照)。そして、第9行目で、その面の方向と視線のベクトルの内積を調べて、面が視線に対して表向きか裏向きかを判定します。

なお、スクリプト第8行目は、面の方向(垂線)のベクトル(変数direction3D)を、Vector3D.normalize()メソッド(前掲シンタックス06-005)で長さ(大きさ)1の単位ベクトルにしています。ベクトルの演算では、その対象を単位ベクトルにすると扱いやすくなることが少なくありません。ただ、このスクリプトではとくに単位ベクトルにする必要はなく、このステートメントを除いても動きは変わりません。

関数xIsFront()は、面と視線のベクトルを調べて、ふたつが向合っていれば(鈍角)表向きのtrueを、同じ方向(鋭角)であれば裏向きのfalseを返します。視線をz軸正の奥向きとすると、面がz軸の負(手前)に向いていれば(鈍角で)表、正(奥)の方向なら(鋭角で)裏ということです(図06-014はy軸の上から見たz-x平面)。

図06-014■視線と面のふたつの方向のベクトルから面の裏表を決める
面と視線のベクトルのふたつが向合って(鈍角)いれば表、同じ方向(鋭角)であれば裏。

本章の最初に書いた前掲スクリプト06-001と同じように、真正面向きの正方形の4頂点を定め(再掲図06-002)、頂点番号0から2の3点で関数xIsFront()の戻り値を確かめてみましょう。視線の方向は、z軸正方向の単位ベクトル(0, 0, 1)とします。つぎのフレームアクションはtrueを返し、面は表向きであることが示されます。

var nUnit:Number = 50;
var view:Vector3D = new Vector3D(0, 0, 1);
var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
vertices.push(new Vector3D(-nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, -nUnit, 0));
vertices.push(new Vector3D(nUnit, nUnit, 0));
trace(xIsFront(vertices, view));   // 出力: true
図06-002■3次元空間に正方形の座標を定める(再掲)
1辺の半分の長さを変数nUnitとして、原点を中心に4頂点を定める。z座標値は0。

スクリプト06-004で定義した関数を、アニメーションに活かしてみましょう。前掲スクリプト06-002で正方形のワイヤーフレームを、マウスポインタの動きに合わせて水平に回しました(再掲図06-006)。この正方形の表と裏に、違う色を塗ることにします。

図06-006■四角形のワイヤーフレームが透視投影されて回る(再掲)


Vector3Dオブジェクトの3次元座標を透視投影したうえで、ワイヤーフレームが描かれている。

SpriteインスタンスのSprite.graphicsプロパティに対してGraphicsクラスの描画メソッドを使うとき、塗り色はGraphics.beginFill()メソッドで設定します。また、塗りを終えるには、Graphics.endFill()メソッドを用います(シンタックス06-006)。

シンタックス06-006■Graphicsクラスの塗りを設定するメソッド
Graphics.beginFill()メソッド
文法 beginFill(color:uint, alpha:Number = 1.0):void
概要 以降の描画に対して適用される単一色の塗りを指定する。
引数

color:uint ― 塗りのRGBカラーを示す0以上の整数。通常は16進数で指定する。

alpha:Number ― 塗りのアルファ値を示す比率。0から1までの数値で指定する。デフォルト値は1(完全な不透明)。
戻り値 なし。
Graphics.endFill()メソッド
文法 endFill():void
概要 閉じられていないパスは閉じて、塗りを適用する。
引数 なし。
戻り値 なし。

前掲スクリプト06-002の回る正方形の表にはシアン(0x00FFFF)、裏に青(0x0000FF)を塗る新たなフレームアクションは、スクリプト06-005として後に掲げました。ワイヤーフレームを描く関数xDrawLines()に、第2引数として表か裏かを示すブール(論理)値(bFront)が加わっています。

  1. function xDrawLines(vertices2D:Vector.<Point>, bFront:Boolean):void {
  2.   var nLength:uint = vertices2D.length;
  3.   var myPoint:Point = vertices2D[nLength - 1];
  4.   var nColor:uint = bFront ? 0x00FFFF : 0x0000FF;
  5.   myGraphics.clear();
  6.   myGraphics.beginFill(nColor);
  7.   myGraphics.lineStyle(2, 0);
  8.   myGraphics.moveTo(myPoint.x, myPoint.y);
  9.   for (var i:uint = 0; i < nLength; i++) {
  10.     myPoint = vertices2D[i];
  11.     myGraphics.lineTo(myPoint.x, myPoint.y);
  12.   }
  13.   myGraphics.endFill();
  14. }

スクリプト第56行目で、第2引数の値により塗り色を定めます。条件に応じて返す式(値)を変える処理には、条件(三項)演算子?:を用いました。

条件 ? 条件がtrueの場合の式 : 条件がfalseの場合の式

[*筆者用参考] Maniac! 02-002「条件判定で最大値と最小値を限定する」

第58行目は、Graphics.beginFill()メソッドにより、そのカラー値を塗りに指定します。そして、第65行目でGraphics.endFill()メソッドを呼出して塗り終えます。

前掲スクリプト06-004で定義した面の表裏を調べる関数xIsFront()は、そのまま加えてあります(スクリプト06-005第31〜41行目)。また、その関数xIsFront()の第2引数に渡す視線のベクトルは、Vector3D型の変数(view)として第7行目に宣言しました。

あとは、これらの修正・追加に対応したリスナー関数xRotate()の書替えです(第16〜22行目)。まず、第19行目で関数xIsFront()を呼出して、面の表裏を表すブール値を得ます。そのうえで、第21行目の関数xDrawLines()の呼出しに、その値を第2引数として加えています。

スクリプト06-005■正方形の表裏に違う塗りを設定してマウスポインタに応じて水平に回す
    // フレームアクション
  1. var nUnit:Number = 100 / 2;
  2. var nDeceleration:Number = 0.3;
  3. var mySprite:Sprite = new Sprite();
  4. var myGraphics:Graphics = mySprite.graphics;
  5. var vertices:Vector.<Vector3D> = new Vector.<Vector3D>();
  6. var nFocalLength:Number = nUnit * 10;
  7. var view:Vector3D = new Vector3D(0, 0, 1);
  8. addChild(mySprite);
  9. mySprite.x = stage.stageWidth / 2;
  10. mySprite.y = stage.stageHeight / 2;
  11. vertices.push(new Vector3D(-nUnit, -nUnit, 0));
  12. vertices.push(new Vector3D(nUnit, -nUnit, 0));
  13. vertices.push(new Vector3D(nUnit, nUnit, 0));
  14. vertices.push(new Vector3D(-nUnit, nUnit, 0));
  15. addEventListener(Event.ENTER_FRAME, xRotate);
  16. function xRotate(eventObject:Event):void {
  17.   var nRotationY:Number = mySprite.mouseX * nDeceleration;
  18.   xTransform(vertices, nRotationY);
  19.   var bFront:Boolean = xIsFront(vertices, view);
  20.   var vertices2D:Vector.<Point> = xGetVertices2D(vertices);
  21.   xDrawLines(vertices2D, bFront);
  22. }
  23. function xTransform(myVertices:Vector.<Vector3D>, myRotation:Number):void {
  24.   var nLength:uint = myVertices.length;
  25.   var myMatrix3D:Matrix3D = new Matrix3D();
  26.   myMatrix3D.appendRotation(myRotation, Vector3D.Y_AXIS);
  27.   for (var i:int = 0; i<nLength; i++) {
  28.     myVertices[i] = myMatrix3D.transformVector(myVertices[i]);
  29.   }
  30. }
  31. function xIsFront(myVertices:Vector.<Vector3D>, myView:Vector3D):Boolean {
  32.   var vector3D_0:Vector3D = myVertices[0];
  33.   var vector3D_1:Vector3D = myVertices[1];
  34.   var vector3D_2:Vector3D = myVertices[2];
  35.   var vector3D_0_1:Vector3D = vector3D_1.subtract(vector3D_0);
  36.   var vector3D_0_2:Vector3D = vector3D_2.subtract(vector3D_0);
  37.   var direction3D:Vector3D = vector3D_0_2.crossProduct(vector3D_0_1);
  38.   direction3D.normalize();
  39.   var bFront:Boolean = (direction3D.dotProduct(myView) < 0);
  40.   return bFront;
  41. }
  42. function xGetVertices2D(myVertices:Vector.<Vector3D>):Vector.<Point> {
  43.   var vertices2D:Vector.<Point> = new Vector.<Point>();
  44.   var nLength:uint = myVertices.length;
  45.   for (var i:uint = 0; i < nLength; i++) {
  46.     var myVector3D:Vector3D = myVertices[i].clone();
  47.     myVector3D.w = (nFocalLength + myVector3D.z) / nFocalLength;
  48.     myVector3D.project();
  49.     vertices2D.push(new Point(myVector3D.x, myVector3D.y));
  50.   }
  51.   return vertices2D;
  52. }
  53. function xDrawLines(vertices2D:Vector.<Point>, bFront:Boolean):void {
  54.   var nLength:uint = vertices2D.length;
  55.   var myPoint:Point = vertices2D[nLength - 1];
  56.   var nColor:uint = bFront ? 0x00FFFF : 0x0000FF;
  57.   myGraphics.clear();
  58.   myGraphics.beginFill(nColor);
  59.   myGraphics.lineStyle(2, 0);
  60.   myGraphics.moveTo(myPoint.x, myPoint.y);
  61.   for (var i:uint = 0; i < nLength; i++) {
  62.     myPoint = vertices2D[i];
  63.     myGraphics.lineTo(myPoint.x, myPoint.y);
  64.   }
  65.   myGraphics.endFill();
  66. }

[ムービープレビュー]を見ると、マウスポインタの水平位置に応じて回る正方形には、表がシアンで裏が青の塗りに設定されています(図06-015)。これは、前掲スクリプト06-004から新たに加えた関数xIsFront()で面の向きを調べ、Graphicsクラスのメソッドで塗り色を変えているからです。

図06-015■四角形の表と裏が違う色で塗られて回る


新たに加えた関数xIsFront()で面の向きを調べて、塗り色が変えられている。

Vector3Dクラスは、単独で処理を行うというよりも、3次元座標のデータを管理するために使われることが多いでしょう。また、3次元座標べクトルの考え方は、3次元空間を扱う基礎になります。その数学的な意味については、後の数学編で解説します。


○Column 06 数学における3次元べクトルの計算とVector3Dクラスのプロパティおよびメソッド
ベクトルは数学で扱われる考え方です。そこで、数学における基本的な3次元ベクトルの計算とそれに対応したVector3Dクラスのプロパティやメソッドを下表06-004にまとめました。

表06-004■3次元べクトルの演算とそれに対応するVector3Dクラスのプロパティまたはメソッド数
ベクトル演算 演算式 Vector3Dクラスのプロパティ/メソッド 説明
加算 A + B Vector3D.add() ベクトルAにベクトルBを足す
減算 A - B Vector3D.subtract() ベクトルAからベクトルBを引く
スカラー倍(伸縮) nA Vector3D.scaleBy() ベクトルAの長さをn倍する
長さ(大きさ) |A| Vector3D.lengthプロパティ ベクトルAの長さを求める
正規化 A/|A| Vector3D.normalize() ベクトルAの長さを1(単位ベクトル)にする
内積 A・B Vector3D.dotProduct() ベクトルAとベクトルBとの内積を求める
外積 A×B Vector3D.crossProduct() ベクトルAとベクトルBとの外積を求める

[*筆者用参考]「ベクトル」

ベクトルの加減算を行うVector3D.add()とVector3D.subtract()メソッドは、もっとも基本的な計算です(シンタックス06-005)。複数のベクトルから、別のベクトルを得るときなどに使われます。たとえば、前掲スクリプト06-004第5〜6行目では、平面の頂点座標から、Vector3D.subtract()メソッドによりその平面上のベクトルを求めました。

ベクトルの長さ(大きさ)を得るプロパティVector3D.lengthは、始点と終点の距離を求める場合に使えます(シンタックス06-005)。また、Vector3D.normalize()メソッドでベクトルの長さを1(単位ベクトル)にしておくと、他のベクトル演算の結果が見やすくなったりします(シンタックス06-005)。

Tips 06-002■ベクトルを正規化した場合の内積と外積
角度がθとなるふたつのベクトルAとBは、ともに予め正規化されていたとします。すると、|A| = |B| = 1です。よって、内積A・Bの値と外積A×Bの大きさ|A×B|は、つぎのようにそれぞれcosθおよびsinθになります(シンタックス06-005のVector3D.dotProduct()とVector3D.crossProduct()メソッドの「戻り値」の説明参照)。

A・B = |A||B|cosθ
|A| = |B| = 1のとき、A・B = cosθ

|A×B| = |A||B|sinθ
|A| = |B| = 1のとき、|A×B| = cosθ

ベクトルには、行列と異なり、乗算がありません。その代わりに、乗算に似た計算が定義されています。ひとつは、ベクトルの長さを伸縮するスカラー倍です。メソッドは、Vector3D.scaleBy()になります(シンタックス06-007)。ベクトルの長さを変える目的のほか、ベクトルのxyz各座標値に同じ数を乗じるために使われることもあります(前章Tips 05-003「Vector3Dインスタンスの座標値を実数倍する」参照)。なお、「スカラー」とは、「ベクトル」と異なり方向をもたず、大きさだけの数値を意味します。

乗算に似たその他のベクトル計算は、内積と外積です。その内容は、本文06-03「面が表向きか裏向きかを調べる − ベクトルの外積と内積」にご説明したとおりです。サンプルとしては、前掲スクリプト06-004および06-005を書きました。

シンタックス06-007■ベクトルをスカラー倍するVector3D.scaleBy()メソッド
Vector3D.scaleBy()メソッド
文法 scaleBy(scale:Number):void
概要 参照するVector3Dインスタンスの角度は変えずに、長さ(Vector3D.lengthプロパティ値)を指定された乗数値で伸縮する。Vector3D.wプロパティの値は変わらない。インスタンスの表すベクトルのxyz各座標値に乗数値が掛け算される。
引数 scale:Number ― ベクトルの長さに掛合わせられる乗数値。負の数を指定すると、方向は反転する。
戻り値 なし。

ベクトルの計算の数学的な解説については、後述数学編をお読みください。

[Prev/Next]

作成者: 野中文雄
作成日: 2010年1月7日
Copyright © 2001-2010 Fumio Nonaka.  All rights reserved.