サイトトップ
Director Flash 書籍 業務内容 プロフィール

PR【無料セミナー】
「ActionScript 3.0の3次元表現と数学の基礎」11月30日火曜日開催

Math for ActionScripters

□02 ガウス平面と回転と、時々、e(ネイピア数)

 ActionScript 3.0による三次元表現ガイドブック

03:20あたりから始まる。20:10-23:00は資料の参照先を確かめるため説明を中断しているのでスキップ可。

○02-01 ガウス平面って何？

●マイナス×マイナスはなぜプラス？

  • どうでもいいが……、借金はマイナスではない(mixi日記)
  • そういうふうにできている
    • 数の概念とつじつまが合うようにマイナスの計算を定義した
    • つじつま: 分配法則などの等式の性質
  • つじつまは数直線で捉えられる

●虚数: i×i＝-1

●ガウス(複素)平面(PDF)

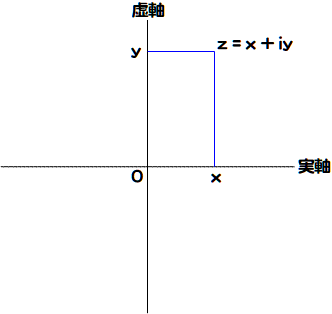
  • 複素数＝実数＋虚数
    • z = x + iy
  • 実数軸(実軸)と虚数軸(虚軸)の直交座標で定められる平面
    • 平面上の点は複素数で示す
    • (x, y)座標と違ってひとつの数で平面が表せる

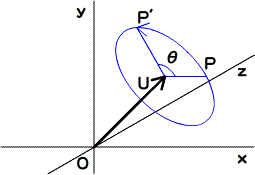
○02-02 ガウス平面と回転

●複素数もiを掛けると半時計回りに90度回転する

  • もちろん-1を掛ければ180度反転

●座標をθ回転させるにはcosθ + i sinθを掛ける(PDF)

  • 複素数の演算はベクトルと似ている
  • ベクトルと違うのは掛け算ができること
  • 複素数の掛け算は回転と伸縮を表す
    • 回転: 角度は足し算
    • 伸縮: 絶対値は掛け算
    • 回転行列(PDF)の役割
      • 2次正方行列×2次元ベクトル: 成分は都合6つ
      • 複素数×複素数: 数字はふたつ
  • 角度θの回転はcosθ + i sinθを掛ける
    • 回転: 角度θ
    • 伸縮: 絶対値1
  • 複素数を拡張して3次元の回転に応用したのが「四元数(クォータニオン)」

○02-03 e(ネイピア数)

●e = 2.71828 18284 59045 23536 02874 71352 …

●eの定義

  • (1 + 1/n)nのnをかぎりなく大きく(∞に)したとき収束する数
    • 年10%の金利(複利)で10年後の元利合計は(1 + 1/10)10倍
    • nを大きくすると利率は少なく期間が長くなる
    • (1 + 1/n)nは((n + 1)/n)nとも書ける

●何とか分の１の確率の物を何とか回やっても起こらない確率

遠藤雅伸氏(@evezoo)
100回試したら一度は起こって欲しい事象に1/100の確率を使う馬鹿多過ぎｗこれを100人で試したら、36人は統計的に100回では起きない概算になる。
  • ゲームの神様「100分の1を100回やってみる」
    「数学的にも、ある回数で１度くらい起こって欲しいことを、『ある回数分の１』 の確率で設定してしまうと、ある回数に達したときにまだ起こっていない人の 割合は、37％弱に収束されます。要するに、何とか分の１の確率の物を何とか回 やっても起こらない人は、100人中36人強になるということ。」
  • 1/nの確率でn回やっても起こらない確率は((n - 1)/n)n
    • 当たりが1/100で外れる確率は99/100 (= (100 - 1)/100)
    • 100回試しても外れる確率は(99/100)100
  • ((n - 1)/n)nの逆数を考える
    • ((n - 1)/n)n
      = (n - 1)n/nn
    • 分子と分母を入替えて
      nn/(n - 1)n
      = (n/(n - 1))n
    • n - 1 = mとおく
      ((m + 1)/m)m + 1
      = (1 + 1/m)m + 1
      = (1 + 1/m)m×(1 + 1/m)1
      = (1 + 1/m)m×(1 + 1/m) … 式(1)
  • ((n - 1)/n)nの逆数(n/(n - 1))nのnをかぎりなく大きくするとeに収束する
    • nをかぎりなく大きくすればmもかぎりなく大きくなる(1の差は関係ない)
    • 式(1)の前項(1 + 1/m)mはeの定義よりeに収束する
    • 式(1)の後項(1 + 1/m)は1に収束する
    • 式(1)はe (= e×1)に収束する
  • 1/nの確率でn回やっても起こらない確率((n - 1)/n)nはeの逆数1/eに収束する
    • 1/e = 1/2.718… = 0.367…
    • 約36.7%

●オイラーの等式

[参考] Yahoo!知恵袋「高校数学の複素関数」


○02-04 補足(質問より)

●「ガウスぼかし」の名前の由来

●ガウスが小学生のときの逸話

  • ある時、1から100までの数字すべてを足すように課題を出された。それを彼は、1 + 100 = 101、2 + 99 = 101、…、50 + 51 = 101 となるので答えは 101×50 = 5050 だ、と即座に解答して教師を驚かせた。
    • [脚注]この逸話は、伝記作家の創作も原因となって様々な形で伝えられており、出題された数列がどのようなものであったかを含めて細部に違いが見られる。
    • 『フェルマーの最終定理』「ガウスの本当の逸話」

●対数螺旋

  • 極座標表示 (r, θ) で
    r = aebθ
  • その他の渦巻

●ネイピア数を見つけたのは

  • ヤコブ・ベルヌーイ

作成者: 野中文雄
更新日: 2010年11月27日 当日の質問にもとづく補足と若干の加筆・補正
作成日: 2010年11月26日
Copyright © 2001-2010 Fumio Nonaka.  All rights reserved.