サイトトップ
Director Flash 書籍 業務内容 プロフィール

Adobe Flash非公式テクニカルノート

任意の座標からもっとも近い線分上の点を求める

ID: FN1104002 Product: Flash CS4 and above Platform: All Version: 10 and above/ActionScript 3.0

任意の座標と線分が与えられたとき、その座標からもっとも近い線分上の点を求めてみましょう。線分は両端が決まっています。両端がなく、長さにかぎりのない直線であれば、座標から直線に下ろした垂線との交点が求める点になります。しかし、線分の場合、垂線が両端の外側を通ると交点はありません。したがって、場合分けをして考えなければならないのです。


01 内積で座標の位置の場合分けともっとも近い線分上の点を求める
線分abの両端に垂線を引きます。すると、ふたつの垂線の内側と、外側に分けられます。内側の座標を点cとし、aを通る垂線の外の座標を点c'、bを通る垂線の外の座標を点c"とします(図001)。

図001■線分の両端に引いた垂線で座標を3つの領域に分ける
図001

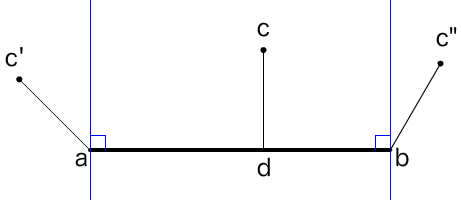
垂線の外側からは、もっとも近い線分上の点は両端の一方になります。つまり、点c'からはa、点c"からはbです。垂線の内側の場合には、座標から線分に下ろした垂線との交点dが求める座標になります。

まずは、点cとc'を切り分けます。点cまたはc'とaを結ぶ線分がabとなす角度をθとします。すると、cosθが負なら垂線の外側、正であれば内側であることがわかります。

図002■線分の端の点aを通る垂線の内側か外側かはcosθの正負でわかる
図002

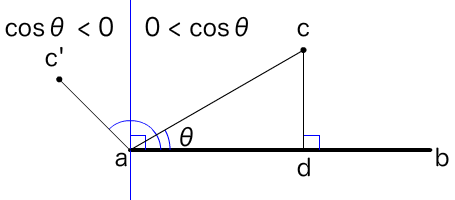
もっとも、∠bac(または∠bac')の角度θをわざわざ求めるのは煩わしいです。cosθの正負は、abを結ぶベクトルPとacのベクトルQとの内積P・Q = |P||Q|cosθの正負と一致します(「Vector3D.dotProduct()メソッド」参照)。さらに、垂線の内側の場合、aから交点dまでの長さadは|Q|cosθとして、内積P・Qから導けます(図003)。

P・Q = |P||Q|cosθ
|Q|cosθ = P・Q / |P|

図003■点cから線分ab上に下ろした垂線との交点dは内積P・Qから導ける
図003

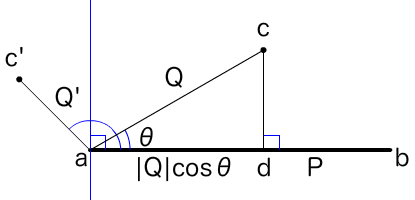
すると、bを通る垂線の外側の点c"については、∠bac"の角度をθ"、ac"のベクトルQ"としたとき、|Q"|cosθは線分abの長さ|P|より大きくなるはずです(図004)。これで、点cとc'およびc"の座標の位置による3つの場合分けもできました。

図004■点c"が点bを通る垂線の外側にあると|Q"|cosθ"は|P|より大きい
図004


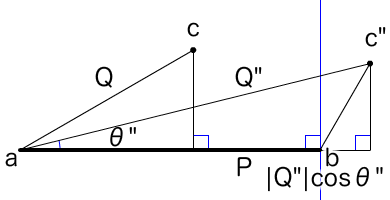
02 任意の1点と線分の両端の座標から線分上のもっとも近い点を返す関数の定義
それでは、任意の1点と、線分の両端の座標をいずれもPointインスタンスで渡し、線分上のもっとも近い点をPointインスタンスで返す関数の定義に移りましょう。前項で述べたとおり、与えられた座標を内積により場合分けし、線分上のもっとも近い点を求めたのがつぎのスクリプト001です。

スクリプト001■任意の1点と線分の両端の座標から線分上のもっとも近い点を返す
    // フレームアクション: メインタイムライン
  1. function xGetClosestPoint(myPoint:Point, begin:Point, end:Point):Point {
  2.   var myVector3D:Vector3D = new Vector3D(myPoint.x - begin.x, myPoint.y - begin.y);
  3.   var baseVector3D:Vector3D = new Vector3D(end.x - begin.x, end.y - begin.y);
  4.   var nDotProduct:Number = myVector3D.dotProduct(baseVector3D);
  5.   if (nDotProduct > 0) {
  6.     var nBaseLength:Number = baseVector3D.length
  7.     var nProjection:Number = nDotProduct / nBaseLength;
  8.     if (nProjection < nBaseLength) {
  9.       baseVector3D.scaleBy(nProjection / nBaseLength);
  10.       return new Point(begin.x + baseVector3D.x, begin.y + baseVector3D.y);
  11.     } else {
  12.       return end;
  13.     }
  14.   } else {
  15.     return begin;
  16.   }
  17. }

まず、前掲図002のcosθによる場合分けです。スクリプト001第2〜3行目で任意の点と線分の両端の都合3点からふたつのベクトル(myVector3DとbaseVector3D)を定め、第4行目がVector3D.dotProduct()メソッドにより内積を求めます。なお、Pointクラスには内積を求めるメソッドがないので、Vector3Dクラスを用いています。その内積の正負を第5行目のifステートメントで調べるにより、ふたつの場合分けができます。

つぎに、前掲図004の内積が正の場合分けに移ります。スクリプト001第6行目が線分の長さ、第7行目は線分の一方の端と任意の点から下ろした垂線との交点までの長さを求めます(前掲図003参照)。第8〜10行目までのifステートメントで、交点までの長さが線分より短い場合に、ふたつの長さの比率を乗じて交点の座標をPointインスタンスにして返します。

そして、スクリプト001第11行目以降は、任意の点からもっとも近い線分上の点がその両端のいずれかになるので(前掲図001参照)、引数として受取ったそれぞれのPointインスタンスをそのまま返しています。


03 ドラッグするインスタンスを折れ線に沿って動かすサンプル
前掲スクリプト001の関数をアニメーションのサンプルに使ってみましょう。複数の座標を結んだ折れ線を描き、その折れ線に沿ってインスタンスがドラッグできるようにします(図005)。

図005■折れ線に沿ってインスタンスがドラッグできる
図004

前掲スクリプト001のフレームアクションに、以下のスクリプト002を書き加えます。このスクリプトの説明は、本稿の主題ではありません。ポイントの処理だけ触れておきます。

第45行目以下の関数xMove()が、スクリプト001の関数xGetClosestPoint()を呼出しています。forステートメントで、Vectorインスタンスに納めたPointエレメントを順にふたつずつ取出し、マウス座標にもっとも近いそれぞれの線分上の点を求めます(第49〜50行目)。その中でマウス座標からの距離が最短になる点に、インスタンスを動かしています(第51〜55行目)。

スクリプト002■ドラッグするインスタンスを折れ線に沿って動かす
    // フレームアクション: スクリプト001に追加
    // 折れ線の座標をPointベース型のVectorインスタンスに加える
  1. var vertices:Vector.<Point> = new Vector.<Point>();
  2. vertices.push(new Point(40, 40));
  3. vertices.push(new Point(80, 60));
  4. vertices.push(new Point(100, 90));
  5. vertices.push(new Point(160, 110));
  6. vertices.push(new Point(200, 140));
    // 描画用Spriteインスタンスの生成とGraphicオブジェクトの取得
  7. var mySprite:Sprite = new Sprite();
  8. var myGraphics:Graphics = mySprite.graphics;
  9. addChildAt(mySprite, 0);
    // 折れ線の描画
  10. myGraphics.lineStyle(1, 0);
  11. myGraphics.moveTo(vertices[0].x, vertices[0].y);
  12. for (var i:uint = 1; i < vertices.length; i++) {
  13.   myGraphics.lineTo(vertices[i].x, vertices[i].y);
  14. }
    // インスタンスを折れ線に沿ってドラッグする
  15. var nStart:Number = new Point(stage.stageWidth, stage.stageHeight).length;
  16. var my_mc:MovieClip;   // ドラッグするMovieClipインスタンスは予め配置
  17. my_mc.x = vertices[0].x;
  18. my_mc.y = vertices[0].y;
  19. my_mc.addEventListener(MouseEvent.MOUSE_DOWN, xStartMove);
  20. function xStartMove(eventObject:MouseEvent):void {
  21.   my_mc.addEventListener(Event.ENTER_FRAME, xMove);
  22.   stage.addEventListener(MouseEvent.MOUSE_UP, xStopMove);
  23. }
  24. function xStopMove(eventObject:MouseEvent):void {
  25.   my_mc.removeEventListener(Event.ENTER_FRAME, xMove);
  26.   stage.removeEventListener(MouseEvent.MOUSE_UP, xStopMove);
  27. }
    // すべての折れ線の中からマウス座標にもっとも近い点にインスタンスを移動する
  28. function xMove(eventObject:Event):void {
  29.   var nClosest:Number = nStart;
  30.   var mousePoint:Point = new Point(mouseX, mouseY);
  31.   var nLength:uint = vertices.length - 1;
  32.   for (var i:uint = 0; i < nLength; i++) {
  33.     var currentPoint:Point =
          xGetClosestPoint(mousePoint, vertices[i], vertices[i + 1]);
  34.     var nDistance:Number = mousePoint.subtract(currentPoint).length;
  35.     if (nDistance <= nClosest) {
  36.       var closestPoint:Point = currentPoint;
  37.       nClosest = nDistance;
  38.     }
  39.   }
  40.   my_mc.x = closestPoint.x;
  41.   my_mc.y = closestPoint.y;
  42. }

作成者: 野中文雄
作成日: 2011年4月21日
Copyright © 2001-2011 Fumio Nonaka.  All rights reserved.