Platform: All
Version: MX and above
Flash MXから、描画メソッドが実装されました。その中で曲線を描くMovieClip.curveTo()メソッドは、コントロールポイントの指定がわかりにくいように思われます。本稿では、このMovieClip.curveTo()メソッドを使って、正円を描くスクリプトをご紹介します。
1. 2次ベジエ曲線
MovieClip.curveTo()は、ベジエ曲線を描くメソッドです。ただし、PostScriptで使用されている、2点の各アンカーポイントにひとつずつコントロールポイントをもつ「3次ベジエ曲線」(Cubic Bezier)ではありません。ふたつのアンカーポイントとひとつのコントロールポイントで曲線を構成する「2次ベジエ曲線」(Quadratic Bezier)を使用します[*1]。
図001■2次ベジエ曲線と3次ベジエ曲線
(ActionScript 2.0リファレンスガイド / ActionScriptクラス / MovieClip / MovieClip.curveTo()メソッドより引用)
2次ベジエは、3次ベシエよりコントロールポイントがひとつ少ないので、プログラム的な扱いは容易です。しかし、3次ベジエのような複雑な曲線を描くことはできません。2次ベジエのコントロールポイントは、両端のアンカーポイントから曲線の接線を延ばし、その交点に置きます[*2]。
図002■MovieClip.curveTo()メソッドのアンカーポイントとコントロールポイントの関係
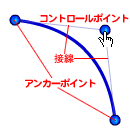
(画像クリックでSWFを表示)
ふたつのアンカーポイントから延ばした接線の交点にコントロールポイントを設定
2. 正円を描く
2次ベジエで完全な正円を描くには、理論上は円周を無限に分割して、アンカーポイントおよびコントロールポイントを設定する必要があります。しかし、実際上は8分割程度で、正円とほとんど区別のつかない近似曲線を描くことが可能です。
以下の関数xDrawCircle()は、描画のターゲットとするMovieClipインスタンスと中心座標、半径、および円周の分割数を引数として、正円の近似曲線を描きます(スクリプト001。サンプルSWF)。
スクリプト001■正円を描く関数(*ActionScript 2.0で記述しています)
|
// [関数] xDrawCircle()
// [引数]
// target_mc:MovieClip 正円を描くターゲットのMovieClipインスタンス
// nX:Number, nY:Number 正円の中心となるxy座標
// nR:Number 正円の半径
// nSegments:Number 近似曲線を描くための円周の分割数(省略可。デフォルトは8)
function xDrawCircle
(target_mc:MovieClip, nX:Number, nY:Number, nR:Number, nSegments:Number):Void {
if (nSegments == undefined) { // 分割数の引数省略時
nSegments = 8; // デフォルト値設定
}
var nAngle:Number = 2*Math.PI/nSegments; // 分割した角度(ラジアン)
target_mc.moveTo(nX+nR, nY);
for (var i = 1; i<=nSegments; ++i) { // 指定数に分割して弧を描画
var nTheta:Number = i*nAngle; // 回転角(ラジアン)
// アンカーポイントの座標
var nAnchorX:Number = nR*Math.cos(nTheta);
var nAnchorY:Number = nR*Math.sin(nTheta);
// コントロールポイントの座標
var nControlX:Number =
nAnchorX+nR*Math.tan(nAngle/2)*Math.cos(nTheta-Math.PI/2);
var nControlY:Number =
nAnchorY+nR*Math.tan(nAngle/2)*Math.sin(nTheta-Math.PI/2);
// 弧の描画
target_mc.curveTo(nControlX+nX, nControlY+nY, nAnchorX+nX, nAnchorY+nY);
}
}
// 正円の描画テスト
// 描画のターゲット用MovieClipを作成
var _mc:MovieClip = this.createEmptyMovieClip("target_mc", 1);
_mc.beginFill(0x00FFFF); // 塗り: シアン
_mc.lineStyle(2, 0x0000FF); // 線: 2ピクセル/青
// ステージ中央を中心に半径100ピクセルの正円を6分割の近似曲線で描画
xDrawCircle(_mc, Stage.width/2, Stage.height/2, 100, 6);
_mc.endFill();
|
上記スクリプト001におけるアンカーポイントとコントロールポイントの求め方を図で示すと、下記のようになります(図003)。ここで円の中心は、原点(0, 0)とします[*3]。三角関数の基礎知識については、Macromedia Flash TechNote「角度と座標の計算 − Flash 5 の三角関数を使う」をお読みください。
図003■アンカーポイントとコントロールポイントの作図
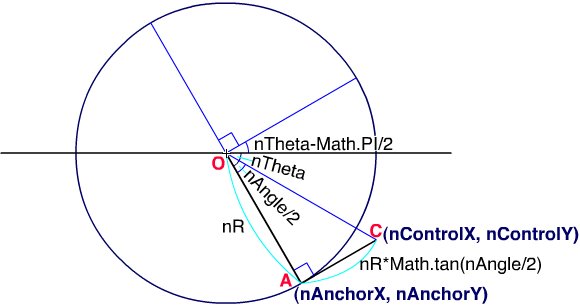
アンカーポイントAを(nAnchorX, nAnchorY)、コントロールポイントCを(nControlX, nControlY)とする
アンカーポイント(A)の座標
OAの長さは円の半径nR、OAがX軸となす角度をnThetaとします。すると三角関数の定義より、アンカーポイントAのxy座標(nAnchorX, nAnchorY)はつぎのとおりです。
nAnchorX = nR*Math.cos(nTheta)
nAnchorY = nR*Math.sin(nTheta)
コントロールポイント(C)の座標
コントロールポイントCは、アンカーポイントAを起点に求めることにします。ACの長さDとACがX軸となす角度Pがわかれば、アンカーポイントAからの座標の差(i, j)は、やはり三角関数の定義から計算できます。
i = D*Math.cos(P)
i = D*Math.sin(P)
スクリプトでは、コントロールポイントは、隣り合うアンカーポイントのちょうど中間に置いています。分割数で割った1回の回転角はnAngleですので、角はその半分のnAngle/2になります。したがって、ACの長さも三角関数の定義より、つぎのとおりになります。
D = nR*Math.tan(nAngle/2)
OAがX軸となす角度は、nThetaです。それを時計と逆、つまり負の方向に90度(π/2ラジアン)回転すれば、ACがX軸となす角度が求まります。ですから、アンカーポイントAとコントロールポイントCとの座標の差は、つぎのとおりです。
i = D*Math.cos(nTheta-Math.PI/2)
= nR*Math.tan(nAngle/2)*Math.cos(nTheta-Math.PI/2)
j = D*Math.sin(nTheta-Math.PI/2)
= nR*Math.tan(nAngle/2)*Math.sin(nTheta-Math.PI/2)
よって、アンカーポイントAの座標に(i, j)を加えれば、コントロールポイントCの座標が求まります。
nControlX = nAnchorX+i
= nAnchorX+nR*Math.tan(nAngle/2)*Math.cos(nTheta-Math.PI/2)
nControlY = nAnchorY+j
= nAnchorY+nR*Math.tan(nAngle/2)*Math.sin(nTheta-Math.PI/2)
|
[*3] Y軸はFlash(コンピュータ)の座標系に合わせて、下を正方向とします。したがって角度も、X軸から時計方向に計ることになります。しかし、数学上の計算は、まったく同じです。「直交座標は、座標軸が垂直に交わってさえいればよいのです。グラフ用紙を上下逆さにしようが、裏返そうが(こうするとFlashの座標系と同じになります)、座標と角度との関係に変わりはないからです」(前掲TechNote)。
[*4] このTechNoteに挿入されている図には、以下のような座標の表記に誤りがあります(図004)。なお「単位円」とは、原点(0, 0)半径1の円を意味します。
図004■単位円上の任意の点をsinおよびcos関数により図示
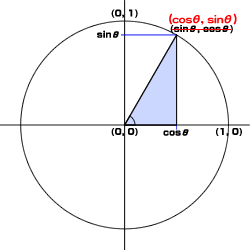
(前掲TechNoteより引用の上修正)
|
_____
作成者: 野中文雄
作成日: 2005年6月17日
