Platform: All
Version: MX and above
直線は、直交座標のグラフに、一次関数として表すことができます。本稿では、この一次関数(方程式)を導くポイントをご紹介します[*1]。
|
[*1] 関数の意味やグラフの描き方については、ThinkQuest@JAPAN「Function++」が参考になるでしょう。
|
1. 直線を式で表す
直線は、xyの直交座標に、xのyに対する一次関数として、つぎのように表されます(図001)[*2]。
y = mx + n
図001■直線の一次関数
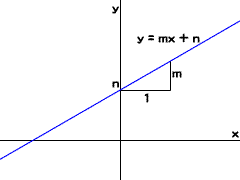
y切片がn、傾きmの一次関数
上記の一次関数y = mx + nで、xが0のときyはnになります。つまり、y軸(x = 0)と値nの点で直線が交わります。この点を「y切片」といいます。yの値はxの値に比例し、m倍の割合で変化します。mは「yの値の変化/xの値の変化」で計算され、xの値が1増加したときyの値はm増加することを意味します。このmは直線の傾き具合を表すので、「傾き」と呼ばれます。
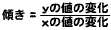
|
[*2] y = mx + nの式では、y軸に平行な直線x = aを表すことができません。したがって、より一般的にはつぎの式で定義されます
ax + by + c = 0
しかし、y = mx + nの式の方が、傾きとy切片から直線の形状を把握しやすいので、広く使われています。
|
2. 指定された点を通る直線の式
指定された点を通る直線の式は、公式として暗記した覚えのある人が少なくないでしょう。けれど、1で述べた直線の一次関数式と傾きの考え方さえ理解すれば、公式はものの1、2分で導けます。つまり、丸覚えする必要はありません。また、考え方を理解する方が、応用範囲も広いといえます。
ポイントは、傾きを考えることです。それではまず、点A(x1, y1)を通る傾きmの直線を求めてみましょう。求める直線上の任意の点をP(x, y)とします。すると、この直線の傾きは、つぎの式で計算できます。
傾き = yの値の変化/xの値の変化 = (y - y1)/(x - x1)
直線の傾きは一定ですので、この値はmに等しくなければなりません。したがって、つぎの方程式が成立ちます。
(y - y1)/(x - x1) = m
y - y1 = m (x - x1)
y = m (x - x1) + y1
点P(x, y)は、直線上の任意の点としました。逆にいえば、この式を満たす(x, y)の集まりが、直線を構成するということになります。つまり、この式が求める直線の方程式です。
公式001■1点と傾きを指定した直線の式
|
点(x1, y1)を通る傾きmの直線は、以下の式で表されます。
y = m (x - x1) + y1
|
つぎに、2点を通る直線の式を考えてみます。2点をA(x1, y1)とB(x2, y2)とします。第1に、点Aを通る訳ですから、直線上の任意の点をP(x, y)としたとき、前述1点を通る直線と同じ傾きの式が導かれます。
傾き = (y - y1)/(x - x1)
第2に、点Aと点Bから、傾きが求められます。
傾き = (y1 - y2)/(x1 - x2)
これらふたつの傾きは、同じ直線の値ですから、当然等しくなければなりません。したがって、以下の方程式が成立ちます。
(y - y1)/(x - x1) = (y1 - y2)/(x1 - x2)
y - y1 = (y1 - y2) (x - x1)/(x1 - x2)
y = (y1 - y2) (x - x1)/(x1 - x2) + y1
公式002■指定した2点を通る直線の式
|
2点(x1, y1)および(x2, y2)を通る直線は、以下の式で表されます。
|
y =
|
y1 - y2
|
(x - x1) + y1
|
|
|
x1 - x2
|
|
3. 直交する直線
ふたつの直線が垂直に交わる場合、一方の直線の傾きをmとすると、もう一方の直線の傾きは-1/mとなります。つまり、ふたつの直線の傾きの積は、-1になります。
公式003■ふたつの直線が垂直に交わる条件
|
傾きmの直線と傾きm'の直線が垂直に交わるとき、つぎの関係が成立ちます。ただし、傾きm≠0とします。
m・m' = -1
あるいは
m' = -1/m
|
このふたつの直線の傾きの関係は、図形的に説明することができます[*3][*4]。
図002■直交する2直線の傾き
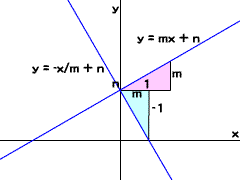
傾きがそれぞれmと-1/mの2直線は直交する
傾きがmの直線は、xの値が1変化すると、yの値はm変化します。傾きが-1/mの直線は、xの値がm変化すると、yの値が-1変化することになります。このふたつの直線の傾きを示した上図002において、ピンクと水色のふたつの直角三角形は、合同になります。直角を挟む2辺の長さが、それぞれ1とmとなっており、互いに等しいからです。
三角形の内角の和は、180度です。したがって、直角三角形の(直角でない)2鋭角の和は、90度になります。上図002で、ふたつの直線の交点は、合同な(ピンクと水色の)ふたつの直角三角形の異なる2鋭角が合わさった角度を成しています。つまり、2直線は直角に交わっているということです。
|
[*3] 中学生にも解ける!大学入試問題(数学)「第8話 どこまでも真っ直ぐなヤツ、彼の名は『直線』!」参照。
[*4] 傾きがmの直線と傾きが-1/mの直線とが直交することを、ベクトルを使って説明することもできます。ベクトルA(1, m)とベクトルB(m, -1)とは、それぞれふたつの直線と傾きが一致します(図003)。
図003■直交する2直線のベクトルで表された傾き
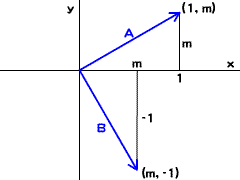
ふたつのベクトルが直交する条件は、内積が0になることです。ベクトルAとベクトルBとの内積は、つぎのように計算されます。
A・B = AxBx + AyBy = 1m + m(-1) = m - m = 0
したがって、ベクトルAとベクトルBとは直交し、これらのベクトルと傾きの等しいふたつの直線も同じように直交します。
|
_____
作成者: 野中文雄
更新日: 2011年2月6日 タイトルに「(方程式)」を追加。
作成日: 2006年3月31日
ドラフト作成: 2006年2月20日