座標は、x軸とy軸が垂直に交わる直交座標で表されることが多いです。けれど、三角関数を用いて、レーダーのように、距離と角度(方向)で位置を示すこともできます。また、座標を位置ベクトルとして扱うことも考えられます。本稿では、同じお題を3つの手法で構成してみます。作成するのは、マウスポインタをイーズアウトしながら追いかけるMovieClipインスタンスのアニメーションです。
図001■マウスポインタをイーズアウトしながら追いかける

1. 座標から位置を計算する
もっともシンプルなのは、xy座標を使って移動先の位置を計算することです。マウスポインタの座標は、DisplayObject.mouseXおよびDisplayObject.mouseYプロパティで調べることができます。これらのプロパティ値をそれぞれインスタンスのDisplayObject.xとDisplayObject.yプロパティに加算すると、インスタンスがマウスポインタと一緒に動きます[*1]。その加算値に減速の比率を乗じることによって、イーズアウトのアニメーションが表現できます(スクリプト001)[*2]。
スクリプト001■インスタンスをマウスポインタに追随させる
|
// フレームアクション
// MovieClip: マウスポインタに追随させるインスタンス
var nDeceleration:Number = 0.2;
addEventListener(Event.ENTER_FRAME, xFollowMouse);
function xFollowMouse(eventObject:Event):void {
x += mouseX * nDeceleration;
y += mouseY * nDeceleration;
}
|
|
[*1] DisplayObject.mouseXおよびDisplayObject.mouseYプロパティの扱いとその注意点については、「ActionScript 3.0で始めるオブジェクト指向スクリプティング」第9回「座標の天動説と地動説」をお読みください。
[*2] イーズアウトのアニメーションについて詳しくは、「ActionScript 3.0で始めるオブジェクト指向スクリプティング」第9回「プロパティのイージング」をご参照ください。
|
2. 三角関数で角度と距離から位置を計算する
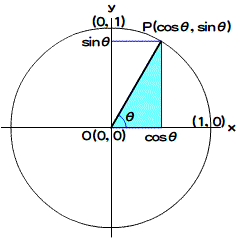
三角関数を用いると、原点から距離が1でx軸と成す角度がθの座標は(cosθ, sinθ)で表されます(図002)[*3]。したがって、距離がrの場合その座標は(r cosθ, r sinθ)です。
図002■距離が1で角度θのxy座標は(cosθ, sinθ)
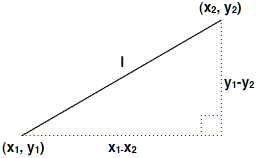
2点間の距離は、三平方の定理を使って求められます。これは直角三角形の斜辺の2乗は、他の2辺の2乗の和に等しいという関係です。2点の座標をそれぞれ(x1, y1)および(x2, y2)とすると、三平方の定理より2点間の距離lはつぎのように導かれます(図003)。
図003■三平方の定理により2点間の距離を求める
| l = √((x1 - x2)2 + (y1 - y2)2) |
 |
数値の累乗にはMath.pow()メソッドを使い、anはMath.pow(a, n)で求められます。平方根を計算するのは、Math.sqrt()メソッドです。また、座標からラジアン値の角度を得るには、Math.atan2()メソッドを用います[*4]。マウスポインタまでの距離と角度を求め、移動先の座標を三角関数で指定したのが、つぎのスクリプト002です。
スクリプト002■インスタンスの座標を三角関数で指定する
|
// フレームアクション
// MovieClip: マウスポインタに追随させるインスタンス
var nDeceleration:Number = 0.2;
addEventListener(Event.ENTER_FRAME, xFollowMouse);
function xFollowMouse(eventObject:Event):void {
var nX:Number = mouseX;
var nY:Number = mouseY;
var nDistance:Number = Math.sqrt(Math.pow(nX, 2) + Math.pow(nY, 2));
var nRadian:Number = Math.atan2(nY, nX);
x += nDistance * Math.cos(nRadian) * nDeceleration;
y += nDistance * Math.sin(nRadian) * nDeceleration;
}
|
前記スクリプト001と比べてステートメント数は増えていますし、このアニメーションについていえば三角関数で処理することによってとくに有利な点もありません。けれどたとえば、ゲームで砲台から砲弾を発射するとか、飛行機を操縦するといった場合には、スビード(フレーム当たりの移動距離)と方向(角度)でインスタンスをコントロールすることが考えられます。そのときの処理は、このスクリプト002の考え方で対応できるのです。
|
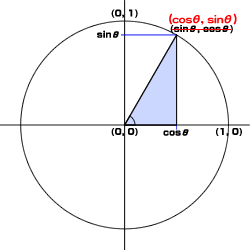
[*3] 座標と三角関数の考え方については、Flash TechNote「角度と座標の計算」をお読みください。ただし、このTechNoteに挿入されている図には、下図004のとおり座標の表記に誤りがあります。
[*4] ラジアンとMath.atan2()メソッドについては、前出注[*3]のTechNoteをご参照ください。
図004■TechNoteの図とその訂正
|
3. ベクトルと極座標を使う
2次元平面のxy座標は、Pointクラスで扱うことができます。Pointクラスでは、位置座標をベクトルと捉えて、ベクトルの演算ができます。前掲スクリプト001の考え方でPointクラスを使うと、以下のスクリプト003のようになります。
Pointインスタンスは、new演算子でコンストラクタメソッドPoint()を呼出し、引数にはxy座標を指定します。Pointインスタンスのベクトルとしての長さを変えるのが、Point.normalize()メソッドです。引数には、長さを数値で指定します。Pointインスタンスの長さは、Point.lengthプロパティで調べられます。現行の長さに減速率を掛けて、イーズアウトした移動位置を算出している訳です。そうして得られたPointインスタンスのxy座標を、MovieClipインスタンスのxy座標にそれぞれ加算しています。
スクリプト003■Pointインスタンスのベクトルとしての長さを変えて位置の算出
|
// フレームアクション
// MovieClip: マウスポインタに追随させるインスタンス
var nDeceleration:Number = 0.2;
addEventListener(Event.ENTER_FRAME, xFollowMouse);
function xFollowMouse(eventObject:Event):void {
var myPoint:Point = new Point(mouseX, mouseY);
myPoint.normalize(myPoint.length * nDeceleration);
x += myPoint.x;
y += myPoint.y;
}
|
Pointクラスでも前掲スクリプト002のように、距離と角度で座標を扱うことができます。2次元平面上の位置を、距離rと角度θにより(r, θ)で表す座標を「極座標」(polar coordinates)といいます。PointクラスにはPoint.polar()メソッドがあり、引数に距離とラジアン値の角度を渡してPointインスタンスが生成できます。つぎのスクリプト004は、Math.atan2()メソッドによりマウスポインタ座標の角度を計算し、Point.polar()メソッドでマウスポインタまでの距離に減速率が乗じられた位置を算出しています。
スクリプト004■Pointクラスで極座標の指定により移動位置を算出
|
// フレームアクション
// MovieClip: マウスポインタに追随させるインスタンス
var nDeceleration:Number = 0.2;
addEventListener(Event.ENTER_FRAME, xFollowMouse);
function xFollowMouse(eventObject:Event):void {
var nX:Number = mouseX;
var nY:Number = mouseY;
var myPoint:Point = new Point(nX, nY);
var nRadian:Number = Math.atan2(nY, nX);
var newPoint:Point = Point.polar(myPoint.length * nDeceleration, nRadian);
x += newPoint.x;
y += newPoint.y;
}
|
イーズアウトのアニメーションは、インスタンスを現在位置と目標位置の間に移動することで表現します。2点を結ぶ線分の中間の座標は、Point.interpolate()メソッドで求めることができます。引数には2点の座標を指定するふたつのPointインスタンスと、ふたつ目のPointインスタンスからの比率を渡します(図005)。
図005■2点の座標を補完するPoint.interpolate()メソッド

Point.interpolate()メソッドにより、マウスポインタの座標とインスタンスの座標の中間座標を求めたのが、以下のスクリプト005です。インスタンスの座標も計算対象とするため、親タイムラインから見た座標値で処理しています。インスタンスの座標からマウスポインタの座標に向かって、減速率の比率の中間座標にインスタンスを移動すれば、イーズアウトのアニメーションになります。
スクリプト005■2点の中間座標として移動位置を求める
|
// フレームアクション
// MovieClip: マウスポインタに追随させるインスタンス
var nDeceleration:Number = 0.2;
addEventListener(Event.ENTER_FRAME, xFollowMouse);
function xFollowMouse(eventObject:Event):void {
var mouse:Point = new Point(parent.mouseX, parent.mouseY);
var myPoint:Point = new Point(x, y);
var newPoint:Point = Point.interpolate(mouse, myPoint, nDeceleration);
x = newPoint.x;
y = newPoint.y;
}
|
Pointクラスには、以上見てきたように、座標の計算をするためのさまざまなプロパティやメソッドが備わっています。座標の演算が多い処理には、Pointクラスを使うと便利な場合があるでしょう。
作成者: 野中文雄
作成日: 2009年5月19日