本章では、三角関数を使って、楕円軌道でアニメーションするMovieClipのフレームアクションを作成します。そのうえで、関数の引数の扱いや、ぼかしフィルタの適用についてご紹介します。
○07-01 バネのような振動のアニメーション
楕円のアニメーションの前に、水平もしくは垂直方向のバネのような振動の動きを、スクリプトで作成してみましょう。バネ運動は、三角関数のcosまたはsintを使って表現できます。
●水平に揺れるアニメーション ー cosを使う
ステージ中央にMovieClipインスタンスをひとつ置き、そのMovieClipシンボルのフレームアクションでまずは単純にcos関数の値を、DisplayObject.enterFrame(Event.ENTER_FRAME)イベントでDisplayObject.xプロパティに設定してみます。cos関数はMathクラスに定義されており、Math.cos()の引数に角度となる数値を渡します。その値を増やしていけば、周期的に増減する数値が返ります。数値は取りあえず0.1ずつ加算することにしましょう(図07-001)。
// MovieClip: 振動させるインスタンス
var nTheta:Number = 0;
addEventListener(Event.ENTER_FRAME, xMoveX);
function xMoveX(eventObject:Event):void {
x = Math.cos(nTheta);
nTheta += 0.1;
}
図07-001■Math.cos()メソッドの戻り値をDisplayObject.xプロパティに設定する

|
Math.cos()メソッドに渡す角度の引数は、毎フレーム0.1ずつ増やす。
|
[ムービープレビュー]を見ると、MovieClipインスタンスは、ステージ左端に移動してしまいます(図07-002)。ただ、よく見るとインスタンスは、わずかに左右に振動しているようです。このスクリプトに少しずつ手を加えながら、三角関数のcosとsinについて説明していきましょう。
図07-002■ステージ左端に移動したMovieClipインスタンス

|
MovieClipインスタンスは、わずかに左右に振動している。
|
cosもsinも数値0を中心に、±1の範囲で値が増減します。ですから、前記スクリプト(図07-001)では、インスタンスが水平座標0のステージ左端に移動し、わずかに±1ピクセルの範囲で水平に揺れ動いたのです。揺れの中心位置を動かしたければその分の座標値を加算すればよいでしょうし、振幅はcos値に幅の数値を乗じれば変えられます。
では、前述のスクリプトに修正を加えて、ステージ中央を中心に左右100ピクセルの幅で揺れ動くように書替えます。対象となるステートメントは、関数xMove()内のDisplayObject.xプロパティへの代入式右辺です。ステージ幅Stage.stageWidthの1/2の値を加え、Math.cos()メソッドの戻り値に100を乗じます。
// MovieClip: 振動させるインスタンス
var nTheta:Number = 0;
addEventListener(Event.ENTER_FRAME, xMoveX);
function xMoveX(eventObject:Event):void {
x = stage.stageWidth/2+Math.cos(nTheta)*100;
nTheta += 0.1;
}
[ムービープレビュー]を確かめると、ステージ中央を中心に左右各100ピクセルの幅で、インスタンスが揺れ動きます。
●垂直に揺れるアニメーション ー sinを使う
今度は、sin関数の値の変化を確かめます。
この処理は、新たに関数xMoveY()を定義して、DisplayObject.yプロパティに設定してみます。上記スクリプトの関数xMoveX()のアニメーションは、一旦コメントアウトして影響を除いておきましょう。もちろん、EventDispatcher.addEventListener()メソッドでリスナー関数にxMoveXを登録したステートメントも、併せてコメントアウトします。この水平のアニメーションの処理は、次節07-02でまた復活させます。
そのうえで、ステージ中央を中心に上下各100ピクセルの範囲を、垂直に揺れ動くスクリプトを書き加えます。三角関数のcosに替えてsinを使い、水平方向のプロパティを垂直方向に修正するほかは、上記スクリプトと基本的に同じ処理です(図07-003)。
// MovieClip: 振動させるインスタンス
var nTheta:Number = 0;
addEventListener(Event.ENTER_FRAME, xMoveY);
function xMoveY(eventObject:Event):void {
y = stage.stageHeight/2+Math.sin(nTheta)*100;
nTheta += 0.1;
}
図07-003■Math.sin()メソッドの戻り値をDisplayObject.yプロパティに設定する

|
水平方向の揺れの処理は、一旦コメントアウトしている。
|
[ムービープレビュー]を見れば、先ほどの水平方向の揺れと同じパターンで、上下各100ピクセルの範囲を垂直に振動するアニメーションが行われます。この動きから想像がつくように、cosとsinは値の増減の仕方、つまり変化のパターンは同じです。違うのは、引数として渡す角度に対して、値が変わるタイミングです。
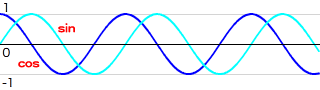
引数の値を0から増加させていったとき、関数の戻り値はcosが1、sinは0からスタートします。そして、引数の値を横軸に、戻り値を縦軸に取ったグラフは、波のようなカーブを描きます(図7-004)。そのため、このふたつの関数は、バネの振動や波の揺れを表現する場合などに用いられます。
図07-004■引数の角度に対するcosとsin値の変化
|
cosとsinのカーブの形状は同じ。波の山と谷の位置がずれている。
|
|
Tips 07-001■位相
cosとsinの値が変わるタイミング、グラフでいえば山と谷の位置の違いは「位相」といいます。よって、cosとsinは位相が異なると表現されます。
|
|
Maniac! 07-001■物理学のバネ運動
物理学では、バネに重りをつけたときの揺れる動きを「単振動」と呼びます。そして、単振動は、sin関数を使った式で表されます。
重りの位置 = 振幅×sin(位相)
重りの位置は、座標値に当たります。振幅は、そのままの意味で、揺れ幅の大きさです。位相は、上図07-004のsinカーブのどこから振動を始めるかということで、重りがどの位置から動くかに相当します。
[*筆者用参考] 物理のかぎしっぽ「単振動〜等速円運動の射影〜」、Wikipedia「振動運動」「単振動」
|
○07-02 円のアニメーションとsinおよびcos
つぎに、円軌道のアニメーションを作成し、三角関数のsinとcosについてももう少し説明します。
●円のアニメーション
先ほど作成した垂直方向の揺れるアニメーションに、また手を入れていきます。一旦コメントアウトしてあった水平方向のアニメーションの処理を復活させ、垂直方向のアニメーションと組合わせてみることにしましょう。ただし、ひとつ修正を加えます。
それは、変数nThetaに値を加算する処理です。前のスクリプトでは、リスナー関数xMoveX()やxMoveY()の中で行いました。ですから、そのままにしておけば、1回のイベントに対して、加算の処理が重複して2回行われてしまいます。
そこで、変数の加算の処理は、また別の関数xUpdate()で行うこととしました。そして、他の関数と同じように、DisplayObject.enterFrame(Event.ENTER_FRAME)イベントのリスナー関数として加えています(スクリプト07-001)。そのほかこの機会に、揺れの中心座標や揺れ幅の値は、変数として宣言しました。
スクリプト07-001■水平方向のcosと垂直方向のsinの揺れを組合わせる
|
// MovieClip: 回転するインスタンス
var nTheta:Number = 0;
var nCenterX:Number = stage.stageWidth/2;
var nCenterY:Number = stage.stageHeight/2;
var nRadius:Number = 100;
addEventListener(Event.ENTER_FRAME, xMoveX);
addEventListener(Event.ENTER_FRAME, xMoveY);
addEventListener(Event.ENTER_FRAME, xUpdate);
function xMoveX(eventObject:Event):void {
x = nCenterX+Math.cos(nTheta)*nRadius;
// nTheta += 0.1;
}
function xMoveY(eventObject:Event):void {
y = nCenterY+Math.sin(nTheta)*nRadius;
// nTheta += 0.1;
}
function xUpdate(eventObject:Event):void {
nTheta += 0.1;
}
|
[ムービープレビュー]で確認してみると、ふたつの揺れの合成は、円の軌跡を描きます。揺れ幅として設定した値(nRadius)は、その円の半径になります。つまり、上記スクリプト07-001は、ステージ中央を中心とした半径100ピクセルの円軌道のアニメーションになるのです(図07-005)。
図07-005■水平方向のcosと垂直方向のsinのアニメーションを組合わせる

|
Tips 07-002■リスナー関数の利点
前記スクリプト(07-001)では、3つの関数をそれぞれ同じDisplayObject.enterFrame(Event.ENTER_FRAME)イベントのリスナー関数として加えました。ほかの構成としては、つぎのようにリスナー関数をひとつ作成して、その中から3つの関数を呼出すというつくり方もできます。
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
xMoveX();
xMoveY();
xUpdate();
}
どちらがよいかは、コンテンツとその仕様により変わってきます。関数をそれぞれイベントリスナーとして扱う方が、関数のパーツとしての独立性は高まります。今回のスクリプト(07-001)でいえば、たとえば水平だけの動きにしたり、垂直だけの揺れに変えることが、ダイナミックに行いやすくなるでしょう。
|
|
AS1&2 Note 07-001■イベントハンドラメソッドとイベントリスナーの比較
ActionScript 2.0/1.0のイベントハンドラメソッドは、ひとつのインスタンスの同じイベントに対して、複数のコールバック関数を設定することはできません(後から設定した関数で、上書きされてしまいます)。ActionScript 3.0のイベントリスナーでは、記述するステートメントが少し増える代わりに、ひとつのインスタンスの同じイベントに対して、複数のリスナー関数を登録できます。
|
●cosとsinの関係
三角関数のcosをDisplayObject.xプロパティに、sinをDisplayObject.yプロパティに設定すると、なぜインスタンスは円軌道を描いて回転するのでしょうか。そんな疑問をもった方には、実も蓋もないお答えをしなければなりません。「そのように定義されている」からです。
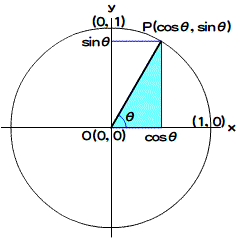
もう少し詳しくいえば、半径1の円周上を動いている点Pがあり、中心Oと点Pとを結ぶ半径OPとx軸との間の角度をθとしたとき、点Pのx座標はcosθ、y座標がsinθと定義されたのです(図07-006)。なお、半径1の円を「単位円」と呼びます。
図07-006■円周上の点を角度に対して定義したのがcosとsin
|
x軸とOPの角度がθのとき、点Pは(cosθ, sinθ)になる。
|
つまり、円周上を動く点(P)のx軸との角度(θ)に対して、点(P)の座標を定めたのがcosとsinなのです。したがって、xy座標にそれぞれcosとsinを指定し、引数に渡す角度を連続的に変えれば、円軌道を描くのは当然です。三角関数のcosとsinについて詳しくは、数学編Math 03「三角関数」の03-01「cos(コサイン)とsin(サイン)」で解説しています。
|
角度に対する円周の座標がcosとsin。だから、cosとsinをxy座標に設定すれば、円軌道になる。
|
前記スクリプト07-001の関数xMoveX()およびxMoveY()内のステートメントで行っている計算は、変化する角度に対して円周上のxy座標を求めていることになります(Tips Math03-002「中心がC(a, b)で半径がrの円の方程式」参照)。
【円周上のxy座標を求める式】
x座標 = 中心のx座標+Math.cos(角度)*半径
y座標 = 中心のy座標+Math.sin(角度)*半径
●ラジアンと度数
三角関数Math.cos()とMath.sin()メソッドの引数となる角度の単位について、ここで確認しておく必要があります。角度は度数でなく、ラジアンという単位で指定しなければなりません。
ラジアンは角度を、半径1の円の円弧の長さで表します(図07-007)。半径1の円の円周は2πです。したがって、360度は2πラジアンになります。
図07-007■ラジアンは角度を半径1の円弧の長さで示す
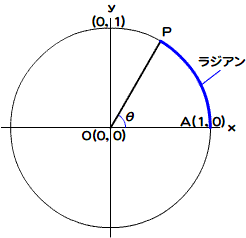 |
360°= 2πラジアン
|
|
∠POAの角度θをラジアンは、半径1の円の円弧PAの長さで表す。
|
他方、DisplayObject.rotationプロパティには度数を単位とする角度を指定しますし、度数で角度を扱いたい場合も少なくないでしょう。そこで、度数とラジアンとの値の変換比率を示しておきます。360度が2πラジアンですので、その比率から以下の式が導かれます。ラジアンについて詳しくは、数学編Math 03「三角関数」の03-03「ラジアン」で解説しています。
度数 = ラジアン×(180/π)
ラジアン = 度数×(π/180)
スクリプト07-001の関数xUpdate()では毎フレーム(DisplayObject.enterFrameイベントのたび)、角度を指定する変数nThetaに0.1ずつ加算していました。単位はラジアンですから、度数に換算すれば約5.73度(=0.1×180/3.14)になります。扱いやすさを考えて、度数の変数nDegreeを新たに宣言し、度数をベースに処理するようにしてみましょう。
スクリプトに変更が加わる部分は、以下のとおりです。毎フレーム加算する角度は、変数nSpeedに5度と設定します。度数をラジアン値に変換する比率(π/180)は、変数nDegreeToRadianに格納しました。
// 変更部分
var nDegree:Number = 0;
var nTheta:Number = 0;
var nSpeed:Number = 5;
var nDegreeToRadian:Number = Math.PI/180;
function xUpdate(eventObject:Event):void {
nDegree += nSpeed;
nTheta = nDegree*nDegreeToRadian;
}
ひとつ気になるのは、変数nDegreeに延々と値を加算し続ける処理です。Number型のデータは充分大きな数値まで扱えるものの、際限なく値を大きくすることには不安が残ります。また、360度以上の角度は、360未満の値に換算することができます。そこで、角度nDegreeの値は、0以上360未満とします。
|
Tips 07-003■Number型データで表せる整数の範囲
Number型データで表せる整数は、-253つまり-9,007,199,254,740,992から253の9,007,199,254,740,992までです(ヘルプ[ActionScript 3.0のプログラミング] > [ActionScript言語とシンタックス] > [データ型] > [データ型の記述]参照)。
|
360度以上の値を360未満の角度に変換するには、その値を360で割った余り(剰余)を求めればよいでしょう。剰余を求めるには、剰余演算子%を用います(Word 05-002「剰余演算子%」参照)。
var nDegree:Number = 810;
trace(nDegree%360); // 出力: 90
今のところ変数nDegreeには、正の値のみが格納されます。しかし、後々処理を拡張したときに、負の数が使われる可能性もあります。ですから、負の値にも対応しておくことにします。
たとえば、-90度は360を加算して270度に換算できます。では、-810度だったらどうでしょう。このときも、一旦360の剰余を取ったうえで、360を加算すればよいのです。負の数に対する360の剰余は、-360より大きく0以下の数値になるからです。
var nDegree:Number = -810;
trace(nDegree%360+360); // 出力: 270
前記の度数をベースとした処理への変更と、角度の値を0から360の範囲に収める処理を加えたのが、以下のスクリプト07-002です。また、度数の値を納めた変数nDegreeとの対比がわかりやすくなるように、変数名nThetaをnRadianに変えました。
スクリプト07-002■角度を度数で扱うように修正
|
// MovieClip: 回転するインスタンス
var nDegree:Number = 0;
var nRadian:Number = 0;
var nSpeed:Number = 5;
var nDegreeToRadian:Number = Math.PI/180;
var nCenterX:Number = stage.stageWidth/2;
var nCenterY:Number = stage.stageHeight/2;
var nRadius:Number = 100;
addEventListener(Event.ENTER_FRAME, xMoveX);
addEventListener(Event.ENTER_FRAME, xMoveY);
addEventListener(Event.ENTER_FRAME, xUpdate);
function xMoveX(eventObject:Event):void {
x = nCenterX+Math.cos(nRadian)*nRadius;
}
function xMoveY(eventObject:Event):void {
y = nCenterY+Math.sin(nRadian)*nRadius;
}
function xUpdate(eventObject:Event):void {
nDegree += nSpeed;
nDegree = (nDegree%360+360)%360;
trace(nDegree); // 確認用
nRadian = nDegree*nDegreeToRadian;
}
|
関数xUpdate()内の処理で変数nDegreeの値を0以上360未満に収めるステートメントは、正負の値に対応させるため、360の剰余を取り360を加算(負の値への対応)したうえで、改めて360の剰余を取っています(正の値への対応)。
関数xUpdate()にはテスト用のtrace()関数を加えましたので、変数nDegreeの値が360より大きくならないことが[出力]パネルで確かめられます。負の値にも対応していることを確認するには、変数nSpeedの値をマイナスに変えてみればよいでしょう。
|
Tips 07-004■スクリプトペイン内を[検索して置換]
[アクション]パネルのスクリプトペインの中で、変数や関数、プロパティ、メソッドなどを検索したり、置換えたりするには、パネルのオプションポップアップメニューから[検索して置換]を選択します。
図07-008■[アクション]パネルのオプションメニューから[検索して置換]


[*筆者用参考] Tips 08-009「[検索して置換]」
|
○07-03 楕円のアニメーション
円のアニメーションに用いた円周上のxy座標を求める式のパラメータを変えると、楕円軌道が描けます。さらに、インスタンスの変形を加えて、3D風に回転するアニメーションを表現してみましょう。
●楕円の軌道を描く式
円周上のxy座標を求める式では、cosとsinの値に半径を掛合わせました。この半径の値をx座標とy座標とで変えると、楕円軌道を描く式になります。
【楕円上のxy座標を求める式】
x座標 = 中心のx座標+Math.cos(角度)*x軸方向の半径
y座標 = 中心のy座標+Math.sin(角度)*y軸方向の半径
たとえば、半径aの円の式について、y軸方向の半径をbに変更します。すると、y座標がすべて中心からb/a垂直移動するため、円はy軸方向にb/aだけ拡大・縮小される結果となり、楕円に変形されます(図07-009)。円と楕円の式について詳しくは、数学編Math 03「三角関数」の03-02「円と楕円の方程式」で解説しています。
図07-009■一方の軸の方向に拡大・縮小を加えると楕円になる
 |
x = a・cosθ
y = b・sinθ
|
|
y軸方向の半径をbにすると、y座標がすべて中心からb/a垂直移動するため、円がy軸方向にb/a変形されて楕円になる。
|
前記スクリプト07-002を楕円軌道のアニメーションにするための変更は、以下のとおりです。x軸方向の半径とy軸方向の半径をそれぞれ新たにnRadiusXとnRadiusYという変数に宣言し、関数xMoveX()とxMoveY()内の座標変換の計算式を修正しています(変数nRadiusはもはや不要ですので削除します)。
// 変更部分
// var nRadius:Number = 100; // 削除
var nRadiusX:Number = 100;
var nRadiusY:Number = 50;
function xMoveX(eventObject:Event):void {
x = nCenterX+Math.cos(nRadian)*nRadiusX;
}
function xMoveY(eventObject:Event):void {
y = nCenterY+Math.sin(nRadian)*nRadiusY;
}
[ムービープレビュー]を確かめるとインスタンスのアニメーションは、中心から水平方向は左右に各100ピクセル、垂直方向には上下各50ピクセルの楕円軌道を描きます(図07-010)。
図07-010■インスタンスのアニメーションは楕円軌道を描く

|
中心から左右各100ピクセル、上下各50ピクセルの楕円軌道になる。
|
●水平スケールを変える
楕円軌道上の位置により水平スケールを変えて、3D風の回転にみえるようにしてみましょう。
インスタンスの大きさを変えるには、2種類のプロパティがあります。それは、DisplayObject.widthおよびDisplayObject.heightと、DisplayObject.scaleXおよびDisplayObject.scaleYの各プロパティの組です。これらは、それぞれ[情報]パネル(または[プロパティ]インスペクタ)と[変形]パネルの設定項目に対応します(表07-001)。
表07-001■インスタンスの大きさを変えるDisplayObjectクラスのプロパティ
| プロパティ:データ型 |
説明 |
対応するパネルの項目 |
|
width:Number
height:Number
|
インスタンスの幅または高さをピクセル単位で示します。
|

|
|
scaleX:Number
scaleY:Number
|
インスタンスの水平または垂直方向のスケール(拡大・縮小率)を示します。ただし、原寸(100%)を1.0とする小数値で指定します。マイナスの数値を設定すると、インスタンスは反転します。
|

|
ふたつのプロパティの組の大きな違いはふたつあります。第1は、単位です。DisplayObject.widthとDisplayObject.heightがサイズをピクセル数で示すのに対して、DisplayObject.scaleXとDisplayObject.scaleYは原寸(100%)を1.0とする小数値で拡大・縮小の比率を指定します。
違いの第2は、負の数値への対応です。DisplayObject.scaleXとDisplayObject.scaleYにマイナスの数値を指定すると、インスタンスが反転します。DisplayObject.widthとDisplayObject.heightには、負の数値は指定できません。
|
Tips 07-005■width/heightとscaleX/scaleYとの連動
DisplayObject.widthおよびDisplayObject.heightプロパティと、DisplayObject.scaleXおよびDisplayObject.scaleYプロパティの値の変更は、相互に連動します。
100×100ピクセルのグラフィックを描いたMovieClipインスタンスに、つぎのようなテスト用のフレームアクションを記述して、その結果を確認してみます。
trace(width, height, scaleX, scaleY); // 出力: 100 100 1 1
width = 200;
trace(scaleX); // 出力: 2
scaleY = 0.5;
trace(height); // 出力: 50
|
今回は、DisplayObject.scaleXを使って、水平スケールを変更します。値としては、sin値をそのまま代入してみます。sin値は楕円軌道上のy座標を計算するときにも使うので、cos値と併せて変数に格納しておきます。変数名は、それぞれnSinおよびnCosとします(スクリプト07-003)。
スクリプト07-003■sin値を水平スケールに設定
|
// MovieClip: 回転するインスタンス
var nDegree:Number = 0;
var nRadian:Number = 0;
var nSpeed:Number = 5;
var nDegreeToRadian:Number = Math.PI/180;
var nCenterX:Number = stage.stageWidth/2;
var nCenterY:Number = stage.stageHeight/2;
var nRadiusX:Number = 100;
var nRadiusY:Number = 50;
var nCos:Number = Math.cos(nRadian);
var nSin:Number = Math.sin(nRadian);
addEventListener(Event.ENTER_FRAME, xMoveX);
addEventListener(Event.ENTER_FRAME, xMoveY);
addEventListener(Event.ENTER_FRAME, xScale);
addEventListener(Event.ENTER_FRAME, xUpdate);
function xMoveX(eventObject:Event):void {
x = nCenterX+nCos*nRadiusX;
}
function xMoveY(eventObject:Event):void {
y = nCenterY+nSin*nRadiusY;
}
function xUpdate(eventObject:Event):void {
nDegree += nSpeed;
nDegree = (nDegree%360+360)%360;
nRadian = nDegree*nDegreeToRadian;
nCos = Math.cos(nRadian);
nSin = Math.sin(nRadian);
}
function xScale(eventObject:Event):void {
scaleX = nSin;
}
|
上記スクリプト07-003においてNumber型の変数nCosとnSinは、関数xUpdate()で角度の値が更新されるときに一緒に設定しています。ただし、この場合変数の初期値に注意しなければなりません。
関数xMoveX()やxMoveY()は、xUpdate()より前にイベントリスナーに登録されていますので、呼出されるのもこれらふたつのリスナー関数の方が先になります。すると、関数xMoveX()とxMoveY()が最初に呼出されるとき、関数xUpdate()の処理はまだ行われていない状態です。したがって、変数nCosとnSinに初期値が与えられていなければ、インスタンスのxy座標が適切に設定されないことになります。
そこで、変数nCosとnSinには初期値として、角度(nRadian)が初期値0のときのそれぞれcosとsinの値を代入してます。これで、関数xMoveX()とxMoveY()の最初の呼出しで、インスタンスは角度0の楕円軌道上に配置されます。
[ムービープレビュー]を見ると、インスタンスが楕円軌道の水平方向両端で幅が0になり、中央で丁度原寸になります。しかも、軌道の上半分では水平方向の向きが左右反転します。そのため、3D風に回転しているように見えます(図07-011)。
図07-011■水平スケールの変形が加わって3D風に回転しているように見える

|
スケールは、両端で幅0で中央が原寸。上半分の楕円軌道では、左右の向きが反転する。
|
このようなアニメーションになるのは、sin値が楕円軌道の中央下側で最大値1、反対に中央の上側で最小値-1を取り、さらに両端では中間の0になるため、3D風の水平スケールの値として丁度よいからです。
○07-04 遠近感をつける ー 関数と引数の扱い
インスタンスのスケールに対する処理をもうひとつ加えましょう。楕円軌道の上にいくほど、インスタンスの水平・垂直スケールを下げて、遠近感をつけてみたいと思います。これも、sin値に連動させる処理です。ただし、今回はsin値をそのまま使う訳にはいきません。
●sin値と連動した値
インスタンスのスケールは、楕円軌道上の垂直座標の最下部では原寸の1、最上部では縮小して0.8にしたいと思います。sin値は最大値が1、最小値は-1ですので、必要なスケールの値の範囲に合わせて換算しなければなりません。
3D風の回転のアニメーションでは、sin値はいわば仮想上のz軸の値となり、値が大きい(下方)ほど手前で、小さい(上方)ほど奥になります。ですから、このsin値に連動した値の換算は、ほかの処理でも使われる可能性があります。そこで、関数xGetIndexZ()として定義することにします。
引数に数値ふたつを指定し、sin値が-1(仮想のzが一番奥)のときの値と、sin値が1(仮想のzが一番手前)のときの値を渡します。たとえば今回は、一番奥で0.8、一番手前では1となる、sin値連動の値が必要なので、つぎのように関数xGetIndexZ()を呼出します。
xGetIndexZ(0.8, 1);
すると、関数xGetIndexZ()は以下のように定義されます。
function xGetIndexZ(nMin:Number, nMax:Number):Number {
var nIndexZ:Number = (nMax-nMin)*(nSin+1)/2+nMin;
return nIndexZ;
}
|
Tips 07-006■ある範囲の数値を別の範囲の数値に対応させる
上記関数xGetIndexZ()では、-1から1までのsin値が保持された変数nSinの値を、引数nMinからnMaxまでの値に変換しています。このようなときは、まずもとの変数の取る値の範囲を、0から1までに変更しておくと便利です。
そのためには、まず最小値が0になるように、値を加算(もしくは減算)します。つぎに、値の範囲の大きさ(1-(-1))で割り、範囲を1に直します。
(nSin+1)/2
そのうえで今度は逆に、対応させる値の範囲の大きさ(nMax-nMin)を乗じ、最小値(nMin)を加算すればよいでしょう。
(nMax-nMin)*(nSin+1)/2+nMin
|
関数xGetIndexZ()を呼出す関数xScale()は、以下のように修正します。まず、第1ステートメントで、水平・垂直のスケール(DisplayObject.scaleXおよびDisplayObject.scaleYプロパティ)をsin値に連動した0.8から1までの値に設定します。
つぎに、第2ステートメントで、水平スケール(DisplayObject.scaleX)をsin値と同じ-1から1までの値で乗じます。*=は、左辺の現在値に右辺値を乗じて代入する算術複合代入演算子です(なお、Tips 01-008「代入の演算子」参照)。
function xScale(eventObject:Event):void {
scaleX = scaleY = xGetIndexZ(0.8, 1);
scaleX *= xGetIndexZ(-1, 1);
}
|
Tips 07-007■複数の変数・プロパティへの値の代入
代入演算子を連続して用いることにより、複数の変数やプロパティに同じ値を代入することができます。
var nOne:Number;
var nTwo:Number;
var nThree:Number;
nOne = nTwo = nThree = 1;
trace(nOne, nTwo, nThree); // 出力: 1 1 1
|
|
Maniac! 07-002■代入式は値を返す
代入式は、右辺値を返します。代入演算子を連続して使うことができるのは、厳密には代入演算子の返す値がその左辺に代入されるからです。
var nOne:Number;
var nTwo:int;
nOne = nTwo = 1.5;
代入式は、右辺から順に実行されます。すると、上記スクリプトの代入式では、まず一番右側の式(nTwo = 1.5)の代入が行われます。変数nTwoはint型ですので、代入値1.5の小数点以下は除かれて、1が格納されます。
しかし、この代入式(nTwo = 1.5)そのものは右辺値1.5を返します。したがって、つぎの代入先の変数nOneには、1.5が代入されることになります。
trace(nOne, nTwo); // 出力: 1.5 1
なお、複合代入演算子は、通常の代入演算子を使ったのと同じ処理とみなされます。したがって、その右辺に記述した値だけでなく、代入される変数値も含まれることにご注意ください。
var nOne:Number;
var nTwo:int = 1;
nOne = nTwo += 1.5;
trace(nOne, nTwo); // 出力: 2.5 2
上記の代入式は、以下のステートメントと同じになり、代入されるのは変数値を含めた値(nTwo+1.5)となります。
nOne = nTwo = nTwo+1.5;
|
前掲スクリプト07-003に上記の関数xGetIndexZ()を追加し、関数xScale()への修正を加えれば、インスタンスが楕円軌道を垂直方向の上にいくほどスケールの縮小するアニメーションになります(図07-012)。
図07-012■楕円軌道を垂直方向の上にいくほどインスタンスのスケールが縮小する

|
インスタンスのスケールは、最下部で原寸の1、最上部では0.8に縮小。
|
●引数の値を確かめる
前記の関数xGetIndexZ()には、もう少し手を加えましょう。それは、関数の引数の扱いです。たとえばテスト用に、つぎのような空の関数xTest()を定義します。
function xTest(n:Number):void {
}
まず第1に、関数内の処理上明らかに不適切な引数は、予め処理から外すようにします。もっとも、引数にはデータ型が指定されていますので、型に合わないデータが渡されればエラーになります(図07-013)。しかし、Number型としてのチェックを通りながら、数値演算処理に不適切な値があります。それは、NaNとundefinedです。
図07-013■引数に指定したデータ型に合わない値をわたすとエラーになる

|
Number型の引数に文字列(String型データ)を渡せば、[コンパイルエラー]が表示される。
|
|
Tips 07-008■変数に型指定をしないと型チェックは行われない
型指定をした引数に変数値を渡す場合、変数宣言でデータ型を指定していないと、型チェックは行われません。
var typed_str:String = "typed";
var untyped_str = "untyped";
function xTest(n:Number):void {
}
xTest(typed_str); // エラー発生
xTest(untyped_str); // エラーなし
|
NaNに対してどのような数値演算を行っても、その結果はNaNにしかなりません(Word 02-003「NaN」参照)。そして、NaNをプロパティに設定すれば、意図しない結果になる場合があります。また、undefinedに対して数値演算を行うと、NaNに変換されます。よって、NaNとundefinedは、数値演算の対象としては適さないのです。
そこで、条件判定によって、NaNとundefinedを処理から切り分けようということになります。このとき覚えておかなければならないのは、NaNには特別な性質があって、等価演算子==などを使った比較では判定できないということです。
var n:Number = NaN;
trace(n == NaN); // 出力: false
NaNであるかどうかを判定するには、isNaN()関数を用いる必要があります。引数に渡した値がNaNのときはtrue、そうでなければfalseを返します。そして、幸いなことに、渡された値がundefinedの場合にもtrueを返すのです。
|
Word 07-001■isNaN()関数
つぎのシンタックスで、式が数値として評価できない値かどうかをブール(論理)値で返します。
sNaN(式:Number):Boolean
isNaN()関数は、渡された引数を数値に変換しようと試みます。その結果数値として評価できず、NaNに変換されるとtrueが返されます。数値に変換できれば、falseを返します。
この関数を使う理由は、数値演算の対象として適さない値NaNを、等価比較(==演算子)で調べることができないからです。
Number型として受取れるおもなデータについて、数値変換の結果とisNaN()関数の戻り値を下表07-002に掲げます。
表07-002■Number型で受取れるデータの数値変換結果とisNaN()関数の戻り値
| 値 |
データ型 |
数値変換結果 |
isNaN()の戻り値 |
|
undefined
|
void
|
NaN
|
true
|
|
null
|
Null
|
0
|
false
|
|
NaN
|
Number
|
そのまま
|
true
|
|
Infinity/-Infinity
|
false
|
|
通常の数値
|
Number/int/uint
|
false
|
[*筆者用参考] ECMA-262「9.3 ToNumber」。
|
|
Maniac! 07-003■NaNは順序づけされない
NaNは、順序づけされない(unordered)特別な値だとされます。それはNumber型の値でありながら、他の数値と比べたとき、(1)その値より小さいか、(2)その値と等しいか、(3)その値より大きいか、のいずれにも当てはまらない状態を意味します。
そのため、不等価演算子(!=と!==)を除き、等価演算子(==と===)や関係演算子(<や>、<=、>=)でNaNとの比較を行うと、NaN自身を含むすべての数値に対してfalseを返します。
trace(NaN == NaN); // 出力: false
trace(NaN != NaN); // 出力: true
[*筆者用参考] IEEE 754浮動小数点演算「順序付けできない(unordered)とは」、Java言語規定「4. 型,値及び変数」「4.2.3 浮動小数点型,フォーマット及び値」。
|
|
Maniac! 07-004■Number型で受取れないデータのisNaN()関数による評価
Number型で受取れない値も、[Strictモード]を解除する(Tips 05-002「等価と厳密な等価」参照)か型指定をしない変数に格納すれば、isNaN()関数に渡して評価することは可能です(ただし、データ型はつねに指定することをお勧めします)。その場合も、数値に変換できるかどうかによって、可能ならfalse、そうでなければtrueが返されます。
たとえば、文字列(String型)の一部は、数値に変換することができます。数字の文字列はその数値に、空文字列""や半角スペース" "は0に変換されます。また、ブール(論理)値(Boolean型)のtrueは1に、falseは0として評価されます。
var n1_str = "1";
var null_str = "";
var bTrue = true;
trace(isNaN(n1_str)); // 出力: false
trace(isNaN(null_str)); // 出力: false
trace(isNaN(bTrue)); // 出力: false
|
それでは、関数xGetIndexZ()に修正を加えて、ふたつの引数について数値演算に不適切な値(NaNとundefined)が指定されていないかどうかの判定を入れます。不適切な値があった場合には、後の処理を行わず、returnステートメントで関数を終了することにします。
ここでは、引数の判定は、その数と同じふたつ必要です。どちらか一方の引数でも不適切な値なら、if条件が満たされたものとします。その場合、ふたつの引数を判定する条件は、論理和演算子||で結びます。
なお、NaN()関数は等価演算子==などを使った論理式ではありません。しかし、論理式と同じように、trueかfalseかのブール(論理)値を返します。また、if条件には、関数や変数を単独で指定することが可能です(Tips 05-003「if条件の評価」参照)。
function xGetIndexZ(nMin:Number, nMax:Number):Number {
if (isNaN(nMin) || isNaN(nMax)) {
trace(nMin, nMax); // 確認用
return NaN;
}
var nIndexZ:Number = (nMax-nMin)*(nSin+1)/2+nMin;
return nIndexZ;
}
関数xGetIndexZ()は戻り値がNumber型で指定されていますので、returnの後にはNumber型の値を置く必要があります(データ型が合わなかったり、戻り値がないとエラーになります)。引数が不適切であることを意味するNumber型の値としては、NaNを返すことにしました。以下のステートメントのように関数xGetIndexZ()を呼出すと、引数の一方がundefinedまたはNaNですので、NaNが返されます。
trace(xGetIndexZ(0, undefined)); // 出力: NaN
trace(xGetIndexZ(NaN, 1)); // 出力: NaN
もっとも、処理が正しく行われているかどうかの確認としては、これでは不十分です。仮に、ifステートメントの処理をそっくり取除いたとしても、関数xGetIndexZ()からはNaNが返されるからです。
なぜなら、上記関数xGetIndexZ()内のローカル変数nIndexZへの代入文で、右辺は引数の値を使って数値演算しています。引数がNaNやundefinedであれば、演算結果はNaNとなり、この値がnIndexZに代入されます。それが関数の戻り値になりますから、ifステートメントがあろうとなかろうと、上記trace()関数の[出力]はNaNになるはずです。
そこで、関数xGetIndexZ()には、ifステートメント内にテスト用として、ふたつの引数をtrace()関数で[出力]するステートメントが加わえられています。ですから、このふたつの引数も併せて[出力]パネルに表示されたら、ifステートメントが正しく処理されたことを確認できます(図07-014)。スクリプトのテストではこのように、場合によっては結果だけでなく、処理過程も確かめる必要があるのです。
図07-014■ifステートメント内に確認用のtrace()関数を追加

|
ふたつの引数がtrace()関数により[出力]されれば、ifステートメントが正しく処理されたことを確かめられる。
|
|

スクリプトは結果オーライではダメ!どこを通ったのかも確かめないと。
|
|
Tips 07-009■論理和演算子||と論理積演算子&&
trueかfalseのどちらかを返すふたつの式AとBがあるとき、どちらか一方でもtrueと評価されればふたつを合わせた結果としてtrueを返すのが論理和演算子||です(表07-003)。それに対して、式AとBがともにtrueのときのみtrueを返すのは、論理積演算子&&になります(表07-004)。
表07-003■論理和演算子||の評価
| 式Aの値 |
式Bの値 |
戻り値(評価) |
| true |
true |
true |
| true |
false |
true |
| false |
true |
true |
| false |
false |
false |
|
表07-004■論理積演算子&&の評価
| 式Aの値 |
式Bの値 |
戻り値(評価) |
| true |
true |
true |
| true |
false |
false |
| false |
true |
false |
| false |
false |
false |
|
条件となる式を3つ以上指定することもできますし、論理和演算子||と論理積演算子&&をともに用いることも可能です。そのような場合には、どの条件式が各演算子の対象(オペランド)なのかを示すように丸括弧()で括ると、スクリプトが見やすくなり、また誤解によるミスも防げます。
たとえば、Dateインスタンスのdateプロパティの値が変数nDateに、dayプロパティ値がnDayに格納されている場合、10日から20日までの間の土曜日か日曜日は以下の条件で判定できます。
if ((10<=nDate && nDate<=20) && (nDay==0 || nDay==6)) {
// 10日から20日までの土曜日か日曜日の場合の処理
}
|
|
Tips 07-010■不適切な値は切り分ける
関数xGetIndexZ()内の処理に「ifステートメントがあろうとなかろうと、上記trace()関数の[出力]はNaNになる」のなら、条件判定は不要ではないかと思われるかもしれません。
しかし第1に、関数の処理に追加や拡張をしていったときに、不適切な値を原因とした不具合が起こらないともかぎりません。また第2に、不適切な値を指定したときに返す値自体が重要なのではなく、その場合の処理を切り分けておくことが大切なのです。そうすれば、必要に応じてエラーを出すようにしたり、適切な値に変更したりといった、対応の処理が後々可能になるからです。
|
|
Maniac! 07-005■論理和演算子||と論理積演算子&&の返す値
ふたつの式AとBをオペランドとして論理和演算子||または論理積演算子&&を用いると、両演算子ともふたつの式をブール(論理)値として評価します。しかし、返す値は必ずしもブール値ではなく、厳密には式AまたはBいずれかの値です。式AやBがブール値を返す場合には、もちろん両演算子の戻り値もブール値になります。
式A || 式B
表07-005■論理和演算子||の戻り値
| 式Aの評価 |
式Bの評価 |
戻り値 |
| true |
true |
式Aの値 |
| true |
false |
式Aの値 |
| false |
true |
式Bの値 |
| false |
false |
式Bの値 |
|
式A && 式B
表07-006■論理積演算子&&の戻り値
| 式Aの評価 |
式Bの評価 |
戻り値 |
| true |
true |
式Bの値 |
| true |
false |
式Bの値 |
| false |
true |
式Aの値 |
| false |
false |
式Aの値 |
|
なお、論理和演算子||は、第1オペランド(式A)がtrueと評価されたとき、第2オペランド(式B)の評価そのものを行いません。したがって、第2オペランドで関数を呼出したり、何らかの処理を行っている場合には、それが実行されなくなりますのでご注意ください。
|
●引数のデフォルト値
引数の扱いの第2として、関数xGetIndexZ()の引数にデフォルト値を与えます。Dateクラスのコンストラクタを引数なしで呼出すと、デフォルトで現在日時のDateインスタンスを作成します(03-04「Dateクラスで日付を調べる」参照)。同じように関数xGetIndexZ()関数の引数にもデフォルト値を設けて、引数なしで呼出したときはsin値がそのまま得られるようにしてみます。
すると、関数xScale()の第2ステートメントで、インスタンスの水平スケールDisplayObject.scaleXを変更している右辺は、つぎのように引数なしに関数xGetIndexZ()が呼出せます。
function xScale(eventObject:Event):void {
scaleX = scaleY = xGetIndexZ(0.8, 1);
scaleX *= xGetIndexZ();
}
|
Tips 07-011■指定された引数を渡さずに関数を呼出すと
関数に引数が指定されている場合、引数を渡さずに関数を呼出すとエラーになります(図07-015)。引数のデフォルト値を指定すると、呼出し時に引数が渡されない場合にはそのデフォルト値が使われるので、エラーが起こらずに済みます。
図07-015■引数が指定されている関数を引数なしに呼出すとエラーになる

|
呼出し時に渡す引数は、関数に定義された引数と数が一致しなければならない。
|
|
関数の引数にデフォルト値を設定するには、以下のように引数の宣言に続けて代入演算子によりデフォルト値を指定します。もちろん、複数の引数に対して、デフォルト値を設定することも可能です。
function 関数名(引数:データ型=デフォルト値):戻り値のデータ型 {
// ステートメント
}
関数xGetIndexY()のふたつの引数についてデフォルトでsin値を返すには、第1引数nMinには-1、第2引数nMaxには1を指定することになります。これで引数なしに関数xGetIndex()を呼出したとき、-1から1までのsin値そのものを戻り値として受取ることができます。
function xGetIndexZ(nMin:Number=-1, nMax:Number=1):Number {
if (isNaN(nMin) || isNaN(nMax)) {
return NaN;
}
var nIndexZ:Number = (nMax-nMin)*(nSin+1)/2+nMin;
return nIndexZ;
}
なお、引数が複数あるときは、その一部にのみデフォルト値を設定することも可能です。ただし、その場合には、デフォルト値は最後の引数から順に定めていく必要があります。たとえば、ふたつの引数を取る関数xTest()の第1引数のみに、デフォルト値を指定したとしましょう。
function xTest(n0:Number=0, n1:Number):void {}
このとき、引数をひとつだけ指定してxTest(1)のように呼出すと、引数は丸括弧()内の順番で決まりますので、第1引数のみ指定したものと認識されます。関数xTest()にはふたつの引数を指定しなければなりませんから、引数の数が合わないというエラーが起こります。
こうなると、引数はつねにふたつ渡さざるを得ず、デフォルト値の出てくる幕はなくなります。ですから、ひとつだけデフォルト値を指定するとすれば、最後の第2引数しか選ぶ余地はないのです。その場合には、引数をひとつだけ渡したとき、第2引数がデフォルト値で補われることになります。
さて、前記スクリプト07-003の関数xGetIndexZ()に、引数の値が適切かどうかのチェックと、デフォルト値の指定を加え、それにともなう修正をしたのが以下のスクリプト07-004です。
スクリプト07-004■関数xGetIndexZ()の引数の扱いを改善
|
// MovieClip: 回転するインスタンス
var nDegree:Number = 0;
var nRadian:Number = 0;
var nSpeed:Number = 5;
var nDegreeToRadian:Number = Math.PI/180;
var nCenterX:Number = stage.stageWidth/2;
var nCenterY:Number = stage.stageHeight/2;
var nRadiusX:Number = 100;
var nRadiusY:Number = 50;
var nCos:Number = Math.cos(nRadian);
var nSin:Number = Math.sin(nRadian);
addEventListener(Event.ENTER_FRAME, xMoveX);
addEventListener(Event.ENTER_FRAME, xMoveY);
addEventListener(Event.ENTER_FRAME, xScale);
addEventListener(Event.ENTER_FRAME, xUpdate);
function xMoveX(eventObject:Event):void {
x = nCenterX+nCos*nRadiusX;
}
function xMoveY(eventObject:Event):void {
y = nCenterY+nSin*nRadiusY;
}
function xUpdate(eventObject:Event):void {
nDegree += nSpeed;
nDegree = (nDegree%360+360)%360;
nRadian = nDegree*nDegreeToRadian;
nCos = Math.cos(nRadian);
nSin = Math.sin(nRadian);
}
function xScale(eventObject:Event):void {
scaleX = scaleY = xGetIndexZ(0.8, 1);
scaleX *= xGetIndexZ();
}
function xGetIndexZ(nMin:Number=-1, nMax:Number=1):Number {
if (isNaN(nMin) || isNaN(nMax)) {
return NaN;
}
var nIndexZ:Number = (nMax-nMin)*(nSin+1)/2+nMin;
return nIndexZ;
}
|
○07-05 ぼかしをかける ー フィルタの適用
遠近感を与えるもうひとつの工夫として、ぼかしをかけてみましょう。仮想のz軸で奥にいくほど、ぼかしの度合いを上げるようにします。
●フィルタの適用手順
Flash CS3ではオーサリング時に、[プロパティ]インスペクタの[フィルタ]タブを使って、インスタンスにフィルタを適用することができます(図07-016)。ActionScriptを使えば、適用するフィルタの種類やパラメータをダイナミックに設定・変更することが可能です。
図07-016■[プロパティ]インスペクタの[フィルタ]タブでインスタンスにぼかしフィルタを適用

|
MovieClipインスタンスに[ぼかし]フィルタを適用。水平と垂直のぼかし幅を、それぞれ設定することができる。
|
スクリプトでぼかしフィルタを適用するには、BlurFilterクラスを使います。ぼかしフィルタ(BlurFilter)にかぎらず、スクリプトでフィルタを適用するには、一般につぎの4つの手順に従います。
【フィルタの適用手順】
- 配列(Array)インスタンスを作成する。
- フィルタインスタンスを作成する。
- フィルタインスタンスを配列インスタンスに格納する。
- インスタンスのDisplayObject.filtersプロパティに配列インスタンスを代入する。
では、この4つの手順にしたがって、簡単なサンプルでぼかしフィルタ(BlurFilterクラス)を設定してみます。スクリプトはメインタイムラインのフレームアクションとし、ぼかしフィルタはタイムラインに置いたMovieClipインスタンスmy_mcに適用するものとします。
//[1]配列を作成
var filters_array:Array = new Array();
//[2]フィルタインスタンスを作成
var myBlur:BlurFilter = new BlurFilter();
//[3]フィルタインスタンスを配列に格納
filters_array.push(myBlur);
//[4]DisplayObject.filtersプロパティに配列を代入
my_mc.filters = filters_array;
図07-017■タイムラインに配置したインスタンスにぼかしフィルタを適用

|
フレームアクションを記述したタイムラインにMovieClipインスタンスmy_mcを配置。フィルタ設定の手順は4つ。
|
[ムービープレビュー]で確かめると、インスタンスにぼかしフィルタがかかっています(図07-018)。BlurFilterインスタンス作成時には、とくに引数(パラメータ)は与えませんでした。その場合は、デフォルト値としてぼかし量が水平・垂直ともに4、品質は[低]に当たる1が適用されます(前掲図07-016の[プロパティ]インスペクタの[フィルタ]タブ参照)。
図07-018■ぼかしフィルタが適用されたインスタンス

|
デフォルトの設定値は、ぼかし量が水平・垂直ともに4、品質は[低]に当たる1。
|
●BlurFilterクラスとDisplayObject.filtersプロパティ
BlurFilter()のコンストラクタに指定する引数の内容については、以下のWord 07-002に解説しました。
|
Word 07-002■BlurFilter()コンストラクタ
つぎのシンタックスで、BlurFilterクラスのインスタンスを作成します。
new BlurFilter(水平ぼかし:Number=4.0, 垂直ぼかし:Number=4.0, 品質:int=1)
*引数の後に代入演算子=で示された値は、デフォルト値を意味します。
引数はすべてオプションで、[プロパティ]インスペクタの[フィルタ]タブにある3つの設定項目にそれぞれ対応します()。
図07-019■[プロパティ]インスペクタの[フィルタ]タブ

|
3つの引数は、[フィルタ]タブにある3つの設定項目に対応する。
|
水平ぼかし ー 水平方向のぼかし量を指定する浮動小数点数値。値の範囲は0から255までで、デフォルトは4です。
垂直ぼかし ー 垂直方向のぼかし量を指定する浮動小数点数値。値の範囲は0から255までで、デフォルトは4です。
品質 ー フィルタの適用回数を指定する正の整数。1が[低]で、2は[中]、3が[高]に相当します。デフォルトは1です。値は最大15まで指定できます。ただし、数値を大きくするほど、描画負荷も高まります。使うのは3までの値にとどめて、さらにぼかしを強くしたいときは、ぼかし量を大きくした方がよいでしょう。
|
|
Tips 07-012■BitmapFilterQualityクラスの定数
BlurFilterインスタンスへの品質の指定には、下表07-007に掲げたBitmapFilterQualityクラスの定数を用いることもできます。
表07-007■BitmapFilterQualityクラスの品質を指定する定数
| 定数 |
品質 |
値 |
| BitmapFilterQuality.LOW |
低品質 |
1 |
| BitmapFilterQuality.MEDIUM |
中品質 |
2 |
| BitmapFilterQuality.HIGH |
高品質 |
3 |
|
なお、フィルタの4つの適用手順は、配列リテラル(06-05「Arrayインスタンス(配列)を使う」参照)を使えば、実際のステートメントとしては2行で済ますこともできます。my_mcはタイムラインに配置されたMoiveClipインスタンスとします。
//[1]フィルタインスタンスを作成
var myBlur:BlurFilter = new BlurFilter();
//[2]フィルタインスタンスが格納された配列をDisplayObject.filtersプロパティに代入
my_mc.filters = [myBlur];
DisplayObject.filtersプロパティには、なぜ直接フィルタインスタンスを設定するのではなく、配列に格納してから代入しなければならないのでしょう。それは、フィルタを複数適用できるようにするためです。
[プロパティ]インスペクタの[フィルタ]タブでも、複数のフィルタが適用でき、それらのフィルタはリストとして表示されます(図07-020)。配列はいわばこのリストの役目を果たし、複数のフィルタインスタンスを格納したうえで、DisplayObject.filtersプロパティに設定することができるのです。
図07-020■[プロパティ]インスペクタの[フィルタ]タブに表示されたフィルタのリスト

|
ひとつのインスタンスに複数のフィルタを適用することができる。
|
適用されたフィルタをすべてクリアするには、DisplayObject.filtersプロパティに空の配列を設定します(my_mcはタイムラインに配置されたMoiveClipインスタンスです)。
my_mc.filters = [];
|
Maniac! 07-006■DisplayObject.filtersプロパティには配列のコピーが設定される
配列はリファレンス型データで、参照渡しでした(Column 06「値と参照」を参照)。すると、DisplayObject.filtersプロパティに空の配列を設定した後でフィルタインスタンスを加えても、インスタンスにフィルタが適用されると予測されLます。
//[1]配列を作成
var filters_array:Array = new Array();
//[2]フィルタインスタンスを作成
var myBlur:BlurFilter = new BlurFilter();
//[3]DisplayObject.filtersプロパティに空の配列を設定
my_mc.filters = filters_array;
//[4]フィルタインスタンスを配列に格納
filters_array.push(myBlur);
しかし、実際にはフィルタの効果が現れません(図07-021)。これは、DisplayObject.filtersプロパティに代入されるのが配列の参照ではなく、内部的に配列のコピーが作成されて、それが設定されるからです。したがって、フィルタを適用するには、つねにDisplayObject.filtersプロパティに配列を代入する操作が必要なのです。
[*筆者用参考] Lott, Schall & Peters『ActionScript 3.0 Cookbook』p.270。
図07-021■DisplayObject.filtersプロパティに空の配列を設定した後にフィルタインスタンスを格納

なお、同様の理由で、DisplayObject.filtersプロパティに対して、直接配列のArray.push()メソッドなどによりフィルタインスタンスを格納しようとしても、フィルタは適用されません。
|
●遠近感をぼかしで表現する
それでは、前掲スクリプト07-004に関数xBlur()を定義して、仮想のz軸で奥にいくほどぼかしを加えるようにしましょう。ぼかし量は仮想z軸のもっとも手前で0、奥が4とします。ただし、水平に動いている雰囲気を出すため、垂直方向のぼかしは量を半分にします。
function xBlur(eventObject:Event):void {
var nBlur:Number = xGetIndexZ(4, 0);
var myBlur:BlurFilter = new BlurFilter(nBlur, nBlur/2);
filters = [myBlur];
}
この関数xBlur()を追加して、DisplayObject.enterFrame(Event.ENTER_FRAME)イベントのリスナーとして登録したのが、以下のスクリプト07-005です。[ムービープレビュー]を見ると、楕円軌道の上部にいくほどぼかしは強まって、遠近感が加わります(図07-022)。
図07-022■BlurFilterクラスでぼかしを加えて遠近感を出す

|
楕円軌道の上部にいくほど、ぼかしの度合いは強まる。
|
スクリプト07-005■関数xBlur()でぼかしをかけて遠近感を出す
|
// MovieClip: 回転するインスタンス
var nDegree:Number = 0;
var nRadian:Number = 0;
var nSpeed:Number = 5;
var nDegreeToRadian:Number = Math.PI/180;
var nCenterX:Number = stage.stageWidth/2;
var nCenterY:Number = stage.stageHeight/2;
var nRadiusX:Number = 100;
var nRadiusY:Number = 50;
var nCos:Number = Math.cos(nRadian);
var nSin:Number = Math.sin(nRadian);
addEventListener(Event.ENTER_FRAME, xMoveX);
addEventListener(Event.ENTER_FRAME, xMoveY);
addEventListener(Event.ENTER_FRAME, xScale);
addEventListener(Event.ENTER_FRAME, xBlur);
addEventListener(Event.ENTER_FRAME, xUpdate);
function xMoveX(eventObject:Event):void {
x = nCenterX+nCos*nRadiusX;
}
function xMoveY(eventObject:Event):void {
y = nCenterY+nSin*nRadiusY;
}
function xUpdate(eventObject:Event):void {
nDegree += nSpeed;
nDegree = (nDegree%360+360)%360;
nRadian = nDegree*nDegreeToRadian;
nCos = Math.cos(nRadian);
nSin = Math.sin(nRadian);
}
function xScale(eventObject:Event):void {
scaleX = scaleY = xGetIndexZ(0.8, 1);
scaleX *= xGetIndexZ();
}
function xBlur(eventObject:Event):void {
var nBlur:Number = xGetIndexZ(4, 0);
var myBlur:BlurFilter = new BlurFilter(nBlur, nBlur/2);
filters = [myBlur];
}
function xGetIndexZ(nMin:Number=-1, nMax:Number=1):Number {
if (isNaN(nMin) || isNaN(nMax)) {
return NaN;
}
var nIndexZ:Number = (nMax-nMin)*(nSin+1)/2+nMin;
return nIndexZ;
}
|
○Column 07 座標の方向に回転させる
xy座標から角度を求めるには、Math.atan2()メソッドを使います。このメソッドを用いて、マウスポインタの方に向かって回転するMovieClipインスタンスのフレームアクションを作成してみましょう。
●座標から角度を返す関数
Math.atan2()メソッドは、一応三角関数のMath.atan()(アークタンジェント)に由来します。しかし、数学には引数(変数)ふたつを取る三角関数はありません。つまり、座標から角度を計算するためにプログラミング上つくられた関数です。
Math.atan2()メソッドには、ふたつの引数y座標とx座標を、この順序で渡します。戻り値はラジアンを単位とする角度です(Word 07-003)。
|
Word 07-003■Math.atan2()メソッド
つぎのシンタックスで、xy座標からラジアン値の角度を返します。
Math.atan2(y座標:Number, x座標:Number):Number
引数には、xy座標のふたつの数値を渡します。y座標、x座標の順番であることにご注意ください。
戻り値は、-πより大きくπ以下のラジアン値の角度です。
なお、このメソッドの意味や由来については、数学編Math 03「三角関数」の03-04「tan(タンジェント)とtan-1(アークタンジェント)」をご参照ください。
|
|

Math.atan2()は、座標から角度が求められる。「三角関数?!」などと難しく考える必要はなし。引数の順序には注意。
|
たとえば、座標(0, 1)は、半径1の単位円がy軸と交わる点ですから、x軸と成す角度は90度になります。Math.atan2()メソッドで計算すると、つぎのとおりです。
var nRadianToDegree:Number = 180/Math.PI;
var nRadian:Number = Math.atan2(1, 0); // 引数の座標がy、xの順であることに注意。
var nDegree:Number = nRadian*nRadianToDegree;
trace(nDegree); // 出力: 90
●インスタンスから見たマウス座標から角度を計算する
インスタンスをマウスポインタの方向に回転させるには、まずインスタンスの基準点からのマウス座標(DisplayObject.mouseX/DisplayObject.mouseYプロパティ)の値を調べて、Math.atan2()メソッドにより角度を計算します。そして、角度のラジアン値を度数に直したうえで、インスタンスの角度(DisplayObject.rotationプロパティ)に設定すればよいでしょう。
すると、インスタンスには、以下のようなフレームアクションを記述すればよさそうに思われます。しかし、[ムービープレビュー]を確かめると、インスタンスが点滅したようなアニメーションになってしまいます。この動きは、04-01「マウス座標を調べる」で天動説と地動説のブロパティを基準の異なるまま設定したときと似ています。
var nRadianToDegree:Number = 180/Math.PI;
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
rotation = Math.atan2(mouseY, mouseX)*nRadianToDegree;
}
しかし、マウス座標の角度を測る原点は、インスタンスの基準点で間違いありません。今回の問題は、インスタンスが回転していることです。インスタンスの座標空間は、インスタンスの角度が変われば、当然それにともなって回転します。
下図07-023ではわかりやすいように、MovieClipシンボルの中にxyの直交座標軸を描きました。まず、インスタンスが回転する前は、x座標は水平でy座標は垂直の状態です。そこにマウスポインタが、たとえば45度の位置にあったとします(図07-023左)。
つぎに、リスナー関数が呼出されて、マウス座標が45度と計算され、インスタンスの角度が45度に設定されます。すると、インスタンスのx軸・y軸も一緒に回転しますので、マウスポインタが動かなかったとしてもインスタンスから見た座標は変わります。マウス座標と同じ45度回転したのですから、マウスポインタはx軸上になったはずです。つまり、マウスポインタの角度は0度になります(図07-023右)。
またリスナー関数が呼ばれると、今度はインスタンスの角度は0に戻されます。この繰返しとなるために、インスタンスが点滅したような動きになったのです。
図07-023■インスタンスから見たマウスポインタの角度をそのままプロパティに設定すると

|
→
|

|
|
インスタンスが回転すると、マウスポインタが動かなくても、異なる角度で認識されてしまう。
|
|
Tips 07-013■インスタンスの座標空間に注意
インスタンスを回転した場合だけでなく、拡大・縮小などの変形を加えたときも、座標空間が変わってきます。位置や距離が、インスタンスの中から見た値と外から測った値とでは、異なる結果になりますので注意しましょう。
|
●インスタンスから見たマウス座標の角度を天動説で設定する
前記のフレームアクションが意図しない動作になった理由はわかりました。すると、解決策は簡単です。自分から見た目的の値は、自分が動くと変わってしまいます。しかし、天動説の考え方を使えば、それは問題にはなりませんでした。
インスタンスから見たマウス座標の角度は、そのまま使います。インスタンスから見た角度というのは、マウス座標の角度と自分の角度との差です。でしたら、その差を埋め合わせれば、目的の値に追いつくことができるはずです。さらに、減速率の変数を加えると、「差を割引いて足し込む」イーズアウトのアニメーションが可能です(04-05「イーズアウトの公式」参照)。
プロパティ += 自分から見た相手との差*減速率
マウスポインタの方向にイーズアウトで回転するインスタンスのフレームアクションは、つぎのスクリプト07-006のとおりです。
スクリプト07-006■インスタンスから見たマウス座標の角度を足し込む
|
// MovieClip: マウスポインタの方向に回転させるインスタンス
var nRadianToDegree:Number = 180/Math.PI;
var nDeceleration:Number = 0.2;
addEventListener(Event.ENTER_FRAME, xRotate);
function xRotate(eventObject:Event):void {
var nRadian:Number = Math.atan2(mouseY, mouseX)*nRadianToDegree;
rotation += nRadian*nDeceleration;
}
|
図07-024■マウスポインタの方向にイーズアウトで回転する

|
「差を割引いて足し込む」イーズアウトの公式は、角度のプロパティに対しても有効。
|
[*筆者用参考] trick7.com blog「Flashで3Dの表現:3Dメニューみたいな」、ProcreoFlashDesign「三角関数を使った円運動」、ささきち流 Suzuka & ParaDraw講座「続々・3D回転メニュー サンプル&作成方法解説」
[Prev/Next]
作成者: 野中文雄
更新日: 2008年3月8日 Word 07-001、002、003のシンタックスを一部修正。
更新日: 2008年3月4日 Word 07-003のMath.atan2()メソッドの戻り値を訂正。
更新日: 2008年1月21日 スクリプトの07-003以降の変数nCosとnSinの初期値を変更。
作成日: 2008年1月18日
















