• 06-01 行列とは
• 06-02 行列のスカラー倍と足し算・引き算
• 06-03 行列の掛け算
• 06-04 変換行列

行列はFlashでも、座標やカラーの変換、一部のフィルタなどに用いられています。本章では、行列の基礎と行列を使った座標変換について、簡単に解説します。

○06-01 行列とは
前章で説明したベクトルは、ひと組の数値を1行で表しました。行列はベクトルを拡張したもので、行に列が加わります。つまり、複数の組の数値がひとつの行列で示せるのです。もっとも、1行でも行列ですので、ベクトルもまた行列のひとつです。

行列のなかの数値ひとつひとつを、行列の「要素」と呼びます。要素は行と列で特定され、変数で示すときには行と列の数値をその順番で添字にすることが多いです。ひとつの行列は、要素すべてを括弧()または[]で括ります。たとえば、2行2列の行列Aは、以下のように示されます。なお、行と列の数が等しい行列は、「正方行列」と呼ばれます。

このあと、行列の計算について説明していきます。しかし、その前に行列とはどういうものなのか、そのイメージをつかんでおきましょう。Flashにおける使い途では、座標やカラーの変換、フィルタなどビットマップのピクセル単位の演算が挙げられます。PhotoshopやFireworksのイメージ調整やフィルタなどでも、内部処理に用いられていると想像されます。つまり、使い方はさまざまで、むしろ使う人が自由に決めてよいのです。

もっとも、これではイメージがわきませんね。数学を例にとると、行列を使えば連立方程式が簡単なひとつの式で表せます。

ax + by = p
cx + dy = q

この連立2元1次方程式は、行列では以下のような式になります。しかも、変数の数はいくつあっても構いません。連立100元1次方程式も、この同じ式なのです。

AX = P

ただし、式は簡単には表せても、実際の解を求める手間は変わりません。私が高校で習ったときも、計算が面倒なせいで、行列は好きではありませんでした。けれど、式の表し方というのは、思いのほか大切です。なぜなら、対象を抽象化することにつながるからです。

以前に小学5年生の娘の算数の授業を参観したときに、こんな問題が出されました。「1mあたり100円のリボンを買って、40mcのリボンを30本用意するにはいくらかかりますか？」 娘を含めて、ほとんどの子は40cmに30を掛け、それをメートルに直していました。

しかし、ひとりの子が、4×3の12m必要で1,200円になると答えました。おとなには当たり前の計算でしょう。0.4×30 = (4÷10)×30 = 4×(30÷10) = 4×3だからです。けれど、初めに10で割った4は長さです。その10で本数を割ってよいのかと、子どもたちには疑問が生じる訳です。

私たちは、ひとたび四則演算の式にしてしまえば、対象が何かを問わず計算規則にしたがって正しい答えが得られることを知っています。行列も、多くの変数や値を扱う計算規則のひとつなのです。

行列で扱える性質をもった数の集まりは、行列に入れてしまえば計算式が簡単になり、まとめて演算できます。もちろん、手計算では大変です。しかし、私たちはコンピュータを使って計算できるのですから、計算式すなわち処理手順が簡単に表せるというのはとても大きなメリットになります。

○06-02 行列のスカラー倍と足し算・引き算
行列はベクトルを拡張したものでした。ですから、性質や計算規則には、共通の部分も少なくありません。まず、行列のスカラー倍は、各要素にそのスカラー値を乗じます。たとえば、2×2(2行2列)の正方行列Aにスカラー値kを掛ける計算はつぎのとおりです。

つぎに、ふたつの行列の足し算と引き算を行うには、ふたつの行と列の数がそれぞれともに等しくなければなりません(正方行列でなくても結構です)。なお、ふたつの行列の行と列の数が等しく、かつ対応する要素(つまり行列Aの要素a_mnと行列Bの要素b_mn)すべてが等しいとき、ふたつの行列は等しいといいます。

ふたつの行列の足し算は、対応する要素をそれぞれ加えます。引き算は逆に、引かれる行列の要素から引く行列の対応する要素をそれぞれ差引きます。引き算は引く方の行列にスカラー値-1を掛け、ふたつの行列を加算すると考えても同じ結果です。

○06-03 行列の掛け算
ベクトルとは異なり、行列には掛け算が定義されています。ふたつの行列を掛け合わせるとき、それらの行と列の数は互いに等しくなくても構いません。しかし、Flashで扱う行列は基本的に正方行列ですので、まずは2×2の正方行列同士の乗算をご説明します。ふたつの4×4の正方行列をAとBの掛け算の結果はつぎのとおりです。

初めて見ると、少し複雑な計算に感じられます。まず、乗算結果の行列の第1行1列目の要素を考えましょう。これは、掛けられる行列Aの1行目と掛ける行列Bの1列目を計算しています。そして、それぞれの値の組をベクトルとみなして、(a₁₁, a₁₂)と(b₁₁, b₂₁)の計算だとすると、ふたつのベクトルの内積(a₁₁b₁₁, a₁₂b₂₁)になっています。つまり、乗算結果の行列の4つの要素は、つぎのように計算されているのです。

行列の乗算では、ふたつの行列の行と列の数が互いに等しい必要はありません。あとで説明する座標変換でよく出てくるのは、正方行列とベクトルとの掛け算です。4×4の正方行列にxy座標の位置ベクトルを乗じる計算は以下のようになります。行列の表現では、ベクトルは1行で示すことも、1列で示すこともできます。

なお、正方行列のうち、左上から右下への対角線の要素(つまりann)がすべて1で、他の要素がすべて0であるものを「単位行列」といいます。単位行列は、Eで表されることが多いです。たとえば、2×2の正方行列では、単位行列はつぎのとおりです。

単位行列は、以下の性質をもちます。数値でいえば1と同じく、掛け算しても値が変化しません。

AE = EA = A

行列の掛け算について、3つ補足しておきます。第1に、交換法則は成立ちません。つまり、AB≠BAです。これは具体的な要素を行列に当てはめて、計算結果を比較すれば簡単に確かめられます。イメージとしては、PhotoshopやFireworksのフィルタで、適用順序を変えると結果の画像が違ってくるのと同じです。

第2に、ふたつの行列の行と列の数は等しくなくてよいものの、どんな行列同士でも乗算できる訳ではありません。掛けられる行列の列数と掛ける行列の行数は等しい必要があります。これは、前述の行列の掛け算の定義からも明らかでしょう。

第3に、ふたつの正方行列を掛け算した結果は、やはり正方行列になります。したがって、正方行列は3つ以上いくつでも掛合わせることができます。前述の例で、2×2の正方行列AにベクトルXを掛合わせた結果はベクトルでした。ですから、この結果のベクトルには、2×2の正方行列もベクトルも乗じることはできません(掛ける順序を逆にして、この結果のベクトルを2×2の正方行列に掛合わせることは可能です)。たとえば、2×2の正方行列A、B、C、Dがあったとすれば、ABCDの掛け算の結果を求めて、さらに2×2の正方行列を乗算することができます。

○06-03 変換行列
位置ベクトルに対して、その次元数と同じ行列数(つまり2次元なら2×2)の正方行列を掛合わせると、原点を中心とした拡大・縮小や回転などの変換が行えます。まず、原点を中心とした拡大・縮小を、行列は使わずに考えてみます。位置ベクトル(x, y)の原点からのの距離をn倍にするには、単純にスカラー値nを乗じて(nx, ny)とするだけです。水平方向にm倍、垂直方向にn倍であれば、位置ベクトルのx、y成分それぞれにスカラー値を掛合わせて、(mx, ny)とすればよいでしょう。

これを、わざわざあえて2×2の正方行列で行うとするなら、つぎのような行列を掛け算します。

つぎに、原点を中心とした位置ベクトルの回転です。前章で、平面上の任意の成分(x, y)をもつベクトルは、スカラー倍した基本ベクトルの和で表せることを説明しました。

(x, y) = x(1, 0)+y(0, 1)

この基本ベクトル(1, 0)と(0, 1)を角度θで回転させれば、平面上の点はその変換に従属してθ回転することになります。三角関数を使えば、変換した基本ベクトルは(cosθ, sinθ)と(-sinθ, cosθ)になります(図Math06-001)。

変換した基本ベクトルは、それぞれ基本ベクトルは(cosθ, sin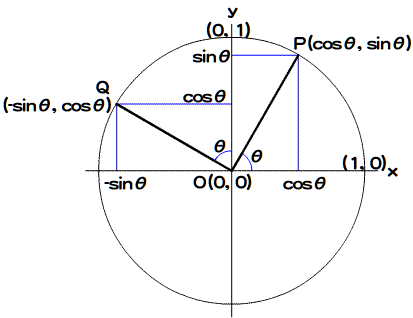θ)と(-sinθ, cosθ)になる。

基本ベクトルを上述のように変換する回転行列は、以下のようなものです。基本ベクトル(1, 0)と(0, 1)を掛合わせて、実際に結果を確かめてみてください。

Maniac! Math53-002■回転行列を求める 回転行列の要素が本文のとおりになることを導くには、三角関数の加法定理を用います。加法定理はつぎのとおりです(証明は省きますので、興味のある人はネットで検索してみてください)。 sin(α+β) = sinαcosβ+cosαsinβ cos(α+β) = cosαcosβ-sinαsinβ 回転の変換を行う前の座標(x, y)は、原点(0, 0)からの距離をr、x軸と成す角度をαとすれば、つぎのように表されます(数学編第03章「三角関数」のとくに図Math03-004参照)。 x = r cosα y = r sinα 原点を中心にこの座標がθ回転されると、回転後の座標(x', y')はつぎのとおりです。 x' = r cos(α+θ) y' = r sin(α+θ) このふたつの式に、前述の加法定理を適用します。 x' = r(cosαcosθ-sinαsinθ) = r cosαcosθ-r sinαsinθ y' = r(sinαcosθ+cosαsinθ) = r sinαcosθ+r cosαsinθ ここで、変換前の座標がx = r cosα、y = r sinαでしたので、これらを代入します。 x' = x cosθ-y sinθ y' = y cosθ+x sinθ = x sinθ+y cosθ

以上で、原点を中心とした拡大・縮小と回転の行列が求められました。しかし、拡大・縮小も回転もせず、単純に移動(平行移動といいます)することができません。そこで、座標を変換する変換行列では、行と列をひとつずつ増やし、3×3の正方行列としました。掛合わせるベクトルも、成分をひとつ増やさなければなりません。ただし、次元を増やすのでなく、定数1を加えます。したがって、変換行列はつぎのように表されます。

すると、平行移動する行列はどのようになるでしょうか。3×3の単位行列をもとにして、t_xとt_yに移動したいx、y座標値(ピクセル数)を当てはめればよいのです。なお、変換後のべクトルで座標値として使うのは、定数1を除いたxy座標のみです。

前述の拡大・縮小や回転についても、基本的にかわるところはありません。変換する必要がない要素については、単位行列のままにしておきます。その結果が、テクニック編第05章05-01「Matrixクラスが表す変換行列」の表Tech05-002の変換行列の値です。

表Tech05-002■変換行列のプロパティ値とその適用結果(再掲)

変換	メソッド	変換行列の値	変換結果
平行移動	translate(ピクセル数x:Number, ピクセル数y:Number):void
拡大・縮小	scale(伸縮率x:Number, 伸縮率y:Number):void
回転	rotate(θ:Number):void
傾斜	−
デフォルト	new Matrix()

これで、座標の拡大・縮小や回転、平行移動が、変換行列という同じかたちで扱えるようになりました。しかし、これらの座標の変換を、わざわざ変換行列にまとめる意味はなんでしょう。その第1は、複雑な変換が行えるということです。現に、傾斜はActionScriptのプロパティやメソッドを使ってはできませんでした。

第2に、変換を自由に組合わせることが可能になります。正方行列は、いくつでも掛合わせられました。ですから、動的に座標変換をつぎつぎに行うことも可能です。また、いくつかの変換を組合わせることにより、単独ではできない処理結果が得られます。PhotoshopやFireworksのフィルタを組合わせるのと同じことです。

たとえば、ここまでの解説を読んで、原点以外を中心とした拡大・縮小や回転ができないのではないかと心配する人もいるかもしれません。たしかに、単独の変換ではできません。それは、変換の組合わせにより解決できるのです。

原点以外を中心に行いたい変換行列をPとしましょう。そして、その原点以外の中心を原点に平行移動する変換行列をT、その位置をもとに戻す変換行列をT'とすれば、以下の行列の掛け算をすればよいのです。

TPT'

この結果得られた行列に座標を掛合わせれば、原点以外を中心とした変換が行えます。

このように行列で数値を扱うと、まとめて計算ができるとともに、処理を組合わせやすくなるという利点があるのです。

[Prev/Next]

---

作成者: 野中文雄
作成日: 2008年8月20日