サイトトップ
Director Flash 書籍 業務内容 プロフィール

Adobe Flash CS3 Professional ActionScript 3.0

□Math 05 ベクトル

ベクトルは運動や座標空間の扱いに用いられます。本章では、ベクトルの基本的な性質とその計算の規則についてご説明します。

○05-01 ベクトルとスカラー
ベクトルはスカラーと対比されます。ベクトルは大きさと向きをもつのに対して、スカラーには大きさしかありません。スカラーは正負の符号をもつ数直線上の点で示され、ベクトルは座標空間上に始点と終点をもった値として表されることが多いです。

表Math05-001■ベクトルとスカラー
値 性質
ベクトル 大きさと向きをもつ。座標空間上に始点と終点をもった値として表される。
スカラー 大きさしかない。正負の符号をもつ数直線上の点で示される。

Tips Math05-001■抽象化されたベクトルとスカラー
数学は抽象化の学問です。抽象化することによって、その理論を適用できる範囲が広がります。ベクトルについても、「方向」にこだわる必要はありません。したがって、複数の数値の組で表され、以降に説明する演算法則にしたがうものがベクトルだと定義されます。これに対して、スカラーはひとつの数値で示されます。

「方向」という意味づけをなくせば、3次元を超えるベクトルも考えることができます。また、次章で説明する「行列」は、ベクトルのベクトルと捉えることができます。

[*筆者用参考] Wikipedia「幾何ベクトル」、「ベクトル空間」。

ベクトルは大きさと向きをもちます。しかし、始点は問いません。つまり、始点が異なっても、向きが等しく平行で、長さの等しいベクトルは、互いに等しいことになります。そこで、ベクトルは、始点を原点とした終点の座標値で表すことができます。このように原点を始点とするベクトルは「位置ベクトル」と呼ばれます。位置ベクトルの終点の各座標値は、ベクトルの「成分」といいます。

図Math05-001■等しいベクトルと位置ベクトル
ベクトルAとベクトルBは、互いに大きさと向きが同じなので等しい。始点の位置は問わない(左図)。位置ベクトルPは、原点Oを始点とする(右図)。

○05-02 ベクトルの絶対値とスカラー倍および単位ベクトル
ベクトルの絶対値とは、ベクトルの長さを表します。2次元のベクトルPが位置ベクトル(x, y)で示されるとき、その絶対値|P|は三平方の定理(数学編第02章「三平方(ピタゴラス)の定理」参照)からつぎのように求められます。

3次元のベクトルでも、同じように三平方の定理から絶対値が導けます(図Math05-002)。その式は2次元と同じく、各成分の2乗の和になります。

図Math05-002■3次元ベクトルの絶対値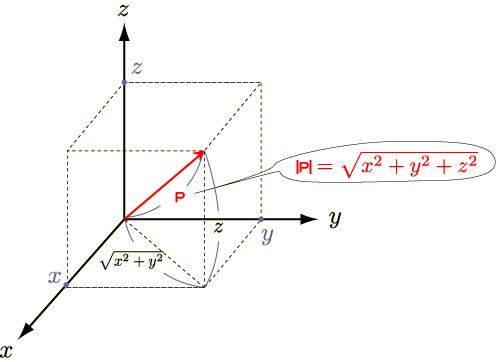

3次元のベクトルでも、その絶対値は三平方の定理より、各成分の2乗の和になる。

[*筆者用参考] 図は物理のかぎしっぽ「もう一度ベクトル1」より一部修正して引用。

Maniac! Math05-001■N次元ベクトルの絶対値
任意の次元つまりN次元ベクトルについても、その絶対値はN個の各成分の2乗和で定義されます。

ベクトルにはスカラーを乗じることができます。その場合、ベクトルの向きは変えずに、長さをスカラー倍します。ただし、負のスカラーを乗じたときは、始点と終点の向きを逆にします。それは結局、ベクトルの各成分にスカラーを掛け合わせるのと同じ結果になります。たとえば、(x, y)で表されるベクトルPにスカラーaを乗じる計算は、つぎの式のとおりです。

aP = (ax, ay)

とくに、大きさが1のベクトルを、「単位ベクトル」と呼びます。Pの単位ベクトルEを求めるには、ベクトルの長さつまり絶対値|P|で割ります(絶対値|P|の逆数1/|P|でスカラー倍するのと同じです)。ただし、ベクトルの絶対値は0ではない(|P|≠0)ものとします。なお、単位ベクトルを求める計算は、ベクトルの「正規化」(normalize)と呼ばれることがあります。

E = P/|P|

Tips Math05-002■Point.normalize()メソッドの正規化
Point.normalize()メソッドは、Pointインスタンスを位置ベクトルとみなして、その長さを引数値の値に変更(伸縮)します(表10-002「Pointクラスのプロパティとメソッド」参照)。Flashでは1ピクセルを単位としてムービーをデザインすることはあまりなく、単位となるピクセル数を任意に定められるようにしたものでしょう。

○05-03 ベクトルの和と差
次元の等しいベクトル同士は、足したり引いたりすることができます。2つのベクトルの和は、それらを2辺とする平行四辺形を描き、その対角までのベクトルで示されます(図Math05-003左図)。差は、引く方のベクトルにスカラー-1を掛けて向きを逆にし、加えればよい(A-B = A+(-B))ことになります(図Math05-003右図)。

図Math05-003■ベクトルの和
ベクトルの和は、2つのベクトルAとBを2辺とする平行四辺形を描き、その対角までのベクトルがA+B(左図)。ベクトルの差は、引く方のベクトルBの向きを逆の-Bにして、ベクトルAに加えればよい(右図)。

ベクトルの成分を使って計算するときは、各成分同士の和あるいは差をとります。ベクトルAを(Ax, Ay)、ベクトルBを(Bx, By)とすると、和および差はつぎのように求められます。

A+B = (Ax+Bx, Ay+By)
A-B = (Ax-Bx, Ay-By)

[*筆者用参考] 物理のかぎしっぽ「もう一度ベクトル2（ベクトルの読み書きそろばん）」。

ベクトルとスカラーの乗除算、およびベクトル同士の加減算については、普通の数値演算と似た以下の法則が成立ちます。任意のベクトルをAとB、同じく任意のスカラーをaならびにbとします。

(a+b)A = aA+bA
(ab)A = a(bA)
A+B = B+A
a(A+B) = aA+aB

x軸y軸に平行な単位ベクトル、(1, 0)と(0, 1)をそれぞれi、jで表すと、任意の成分(x, y)をもつベクトルPは以下の式で示されます。このiとjを「基本ベクトル」といいます。

P = (x, y) = x(1, 0)+y(0, 1) = xi+yj

つまり、平面上の任意の位置ベクトルは、スカラー倍した基本ベクトルの和で表せます。


○05-04 ベクトルの内積
ベクトル同士の演算には乗除算はありません。しかし、乗算に似た計算に「内積」があります。ベクトルAとBとの内積A・Bは、AとBとの成す角をθとすると、以下の式で定義されます(ベクトルでは「・」は内積を意味し、掛け算ではありません)。内積の値はスカラー値であって、ベクトルではないことにご注意ください。

A・B = |A||B|cosθ

cosθは1以上-1未満の値をとります(数学編03-01「cos(コサイン)とsin(サイン)」参照)。cosθが0のときベクトルAとBは直交し、内積A・Bは0(= |A||B|×0)になります。つまり、内積が0になることは、ベクトルAとBとの直交条件なのです。

【ベクトルAとBの直交条件】
A・B = 0

ベクトルAとBの各成分がそれぞれ(Ax, Ay)と(Bx, By)である場合、ふたつのベクトルの内積はつぎの式で計算できることが知られています。

A・B = AxBx+AyBy

内積を表すふたつの式から、ベクトルAとBとの成す角を求めることができます。

|A||B|cosθ = AxBx+AyBy
cosθ = (AxBx+AyBy)/(|A||B|)

Tips Math05-003■3次元以上のベクトルの場合
本章で解説したベクトルの性質や計算規則は、3次元以上のベクトルでも異なりません。むしろ、前掲Tips Math05-001でも触れたとおり、これらの性質と計算規則にしたがう複数の数値の組が、ベクトルとして扱われることになるのです。

Maniac! Math53-002■|A||B|cosθとAxBx+AyByの値
内積A・Bを表すふたつの式、|A||B|cosθとAxBx+AyByの値が等しいことは自明ではありません。それを示すためには、余弦定理を用います。各辺の長さをそれぞれa、b、cとする以下の三角形において、余弦定理はつぎの等式で示されます(余弦定理の証明は省きます。興味がある方はネットで検索すれば、簡単に確かめられるでしょう)。

c2 = a2+b2-2ab cosθ
cosθ = (a2+b2-c2)/2ab

a、b、cは、それぞれベクトルA、B、A-Bの絶対値です。したがって、これらの項を入替えたうえで、上記cosθの式を内積の定義式に代入して、つぎのように変形することができます。

A・B = |A||B|cosθ
= |A||B|(|A|2+|B|2-|A-B|2)/2|A||B|
= (|A|2+|B|2-|A-B|2)/2
= ((Ax2+Ay2)+(Bx2+By2)-((Ax-Bx)2+(Ay-By)2))/2
= (2AxBx+2AyBy)/2
= AxBx+AyBy

[*筆者用参考]「内積の意味」、「『内積の定義』の導入について」。

[Prev/Next]

作成者: 野中文雄
作成日: 2008年8月19日
Copyright © 2001-2008 Fumio Nonaka.  All rights reserved.