|
Math for ActionScripters
□02 ガウス平面と回転と、時々、e(ネイピア数)

○02-01 ガウス平面って何?
●マイナス×マイナス
- どうでもいいが……、借金はマイナスではない
- そういうふうにできている

- 数の概念とつじつまが合うようにマイナスの計算を定義した
- つじつま: 分配法則などの等式の性質
- 数直線で考える
●虚数: i×i=-1
●ガウス(複素)平面
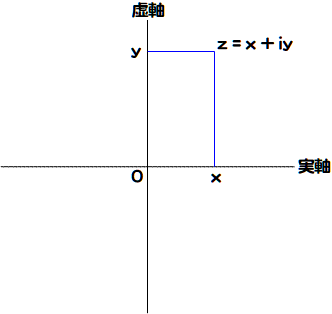
- 複素数=実数+虚数
z = x + iy
- 実数軸(実軸)と虚数軸(虚軸)の直交座標で定められる平面
[参考] Yahoo!知恵袋「高校数学の複素関数」
○02-02 ガウス平面と回転
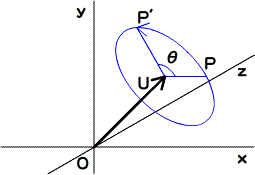
●複素数もiを掛けると半時計回りに90度回転する
●座標をθ回転させるにはcosθ + i sinθを掛ける
○02-03 e(ネイピア数)
●e = 2.71828 18284 59045 23536 02874 71352 …
●eの定義
- (1 + 1/n)nのnをかぎりなく大きく(∞に)したとき収束する数

- 年10%の金利(複利)で10年後の元利合計は(1 + 1/10)10倍
- nを大きくすると利率は少なく期間が長くなる
- (1 + 1/n)nは((n + 1)/n)nとも書ける
●何とか分の1の確率の物を何とか回やっても起こらない確率
遠藤雅伸氏(@evezoo)
100回試したら一度は起こって欲しい事象に1/100の確率を使う馬鹿多過ぎwこれを100人で試したら、36人は統計的に100回では起きない概算になる。
- ゲームの神様「100分の1を100回やってみる」
「数学的にも、ある回数で1度くらい起こって欲しいことを、『ある回数分の1』
の確率で設定してしまうと、ある回数に達したときにまだ起こっていない人の
割合は、37%弱に収束されます。要するに、何とか分の1の確率の物を何とか回
やっても起こらない人は、100人中36人強になるということ。」
- 1/nの確率でn回やっても起こらない確率は((n - 1)/n)n
- 当たりが1/100で外れる確率は99/100 (= (100 - 1)/100)
- 100回試しても外れる確率は(99/100)100
- ((n - 1)/n)nの逆数を考える
- ((n - 1)/n)n
= (n - 1)n/nn
- 分子と分母を入替えて
nn/(n - 1)n
= (n/(n - 1))n
- n - 1 = mとおく
((m + 1)/m)m + 1
= (1 + 1/m)m + 1
= (1 + 1/m)m×(1 + 1/m)1
= (1 + 1/m)m×(1 + 1/m) … 式(1)
- ((n - 1)/n)nの逆数(n/(n - 1))nのnをかぎりなく大きくするとeに収束する
- nをかぎりなく大きくすればmもかぎりなく大きくなる(1の差は?そんなの関係ねぇ)
- 式(1)の前項(1 + 1/m)mはeの定義よりeに収束する
- 式(1)の後項(1 + 1/m)は1に収束する
- 式(1)はe (= e×1)に収束する
- 1/nの確率でn回やっても起こらない確率((n - 1)/n)nはeの逆数1/eに収束する
- 1/e = 1/2.718… = 0.367…
- 約36.7%
●オイラーの等式
作成者: 野中文雄
作成日: 2010年11月25日
Copyright ©
2001-2010 Fumio Nonaka. All rights reserved.
|